Принцип составления уравнений для переменного тока.

Изучить принципы составления уравнения для тока в цепи переменного тока, содержащую индуктивность.

Принцип составления уравнений для переменного тока.

Принцип составления уравнений базируется на трех принципах:

· 2 уравнения Кирхгофа. Реальные цепи являются, как правило, разветвленными, и для них действуют два закона Кирхгофа: первый – для любого узла электрической цепи сумма втекающих в него токов равна сумме вытекающих токов, т.е.

∑i_n = 0;

второй – в любом замкнутом контуре с током алгебраическая сумма э.д.с., встречающихся по ходу тока, равна алгебраической сумме падений напряжений на элементах этого контура:

∑e_k = ∑U_k = i*∑z_k.

· модели элементов цепи (например, зависимость напряжения от тока, U_L = L*(dI/dt), - это модель). Катушка индуктивности включается последовательно в цепь, где есть источник. Используя принцип Кирхгофа, составляем уравнение для этой схемы:

RI + L(dI/dt) = E_m sinwt.

Если индуктивность L не зависит от тока I, то это уравнение будет линейным, если же есть зависимость, то уравнение нелинейное.

· Закон Ома.

Приведем примеры того, как составляются уравнения для переменного тока.

1. Пусть у нас есть неразветвленный контур, содержащий индуктивность, конденсатор и резистор. Для составления уравнения используем второй закон Кирхгофа, т.е. ∑e_k = ∑U_k.

Найдем для каждого элемента цепи его напряжения:

· Для R: U_R = R*i, где i – мгновенное значение тока, т.е. его значение зависит от времени;

· Для L: U_L = L ;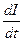

· Для C: U_c = ;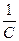

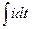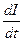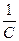
В итоге получим уравнение R*I + L + 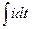= E , где Е – э.д.с. контура. Далее продифференцируем это уравнение по времени, мы можем это сделать, потому что все члены уравнения непрерывны. Получим

L 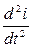+ R + = .

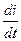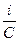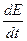Искажение формы тока мы можем наблюдать за счет эффекта нелинейности, который дает элемент индуктивности, т.е. L = L(i), так как µ = F(H).

Решать нелинейные уравнения мы можем различными способами, такими как: Метод Рунге Кутта(1,2,4 порядка), конечно-разностный метод, метод стрельбы и.т.п.

2. Рассмотрим еще один пример, в котором сравним данные, полученные экспериментально и теоретически:

Исследуемая схема имеет вид:

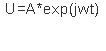
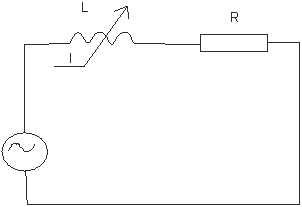
где L(i) – нелинейная индуктивность; R – резистор; U – э.д.с. контура.

Значения R =10 Ом и w = 10 Гц заданы.

Результаты, полученные при проведении измерений, запишем в таблицу:

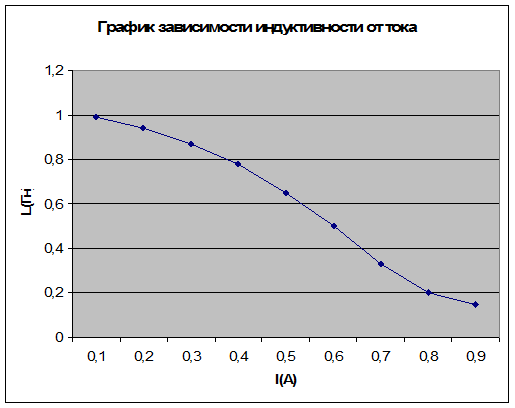
С помощью 2 закона Кирхгофа составим уравнение для этого контура.

RI + L 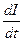= A*e^jwt;

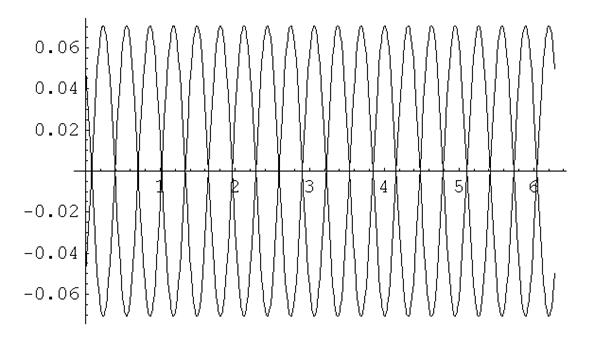
Уравнение неоднородное, т.к. правая часть не равна нулю. Искать решение этого уравнения вручную громоздко, поэтому сделаем это с помощью компьютерной программы Математика. Вводим значения L=1 Гн, R=10 Ом, w=10 Гц, A= 1. Увидим, что графическое решение уравнения, где индуктивность не зависит от величины протекающего по ней тока, будет совершенно неискаженным.