Описание установки и метода измерений

Под математическим маятником понимают идеализированную систему, состоящую из невесомой и нерастяжимой нити, на которой подвешена масса, сосредоточенная в одной точке. В данной работе в качестве математического маятника исполь-зуется массивный свинцовый шарик, подвешенный на двух расходящихся нитях (рис. 10.2). Длину маятника можно изменять, наматывая нить на ось.

Когда маятник отклонен от положения равновесия на угол a (рис. 10.3), силу тяжести 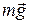, действующую на него, можно разложить на две составляющие: 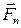, направленную вдоль нити, и 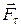, направленную перпендикулярно нити. Составляющая силы тяжести 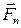уравновешивается силой натяжения нити 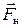, а составляющая 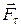остается неуравновешенной. Она возвращает шарик в положение равновесия. Из рисунка видно, что 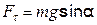. Если угол a мал, то sina примерно равен самому углу a, измеренному в радианах. Т. е. a = х/ 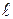, и сила, возвращающая маятник в положение равновесия,

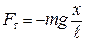, (10.4)

где х – смещение шарика от положения равновесия, 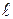– длина нити маятника, знак ²–² показывает, что сила направлена к положению равновесия.

Теперь запишем II закон Ньютона для маятника:

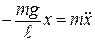, (10.5)

где 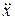– вторая производная от смещения по времени, представляющая собой ускорение маятника.

Введя обозначение

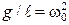, (10.6)

уравнение (10.5) можно переписать в виде

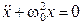. (10.7)

Из уравнения (10.7) следует (это легко проверить подстановкой), что смещение шарика 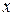представляет собой следующую функцию времени:

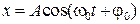, (10.8)

где А и j₀– постоянные интегрирования, определяемые начальными условиями.

Итак, при малых отклонениях маятник движется по закону косинуса (или синуса), т. е. совершает гармоническое колебательное движение. Проанализировав уравнения (10.8), находим, что А – амплитуда колебаний (максимальное отклонение от положения равновесия), j₀ – начальная фаза колебаний (определяет смещение в момент времени t = 0), 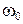– циклическая (или круговая) частота, связанная с периодом колебаний Т соотношением:

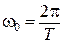. (10.9)

С учетом введенного выше обозначения (10.6) получаем формулу периода гармонических колебаний математического маятника

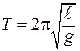. (10.10)

С помощью (10.10) можно определить ускорение свободного падения в данной точке Земли

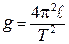. (10.11)

Точность измерения g зависит, главным образом, от точности измерения его длины, так как трудно определить положение центра масс маятника. Период колебаний маятника легко измерить на опыте, определив время t, за которое маятник совершает n колебаний:

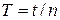. (10.12)