Описание установки и метода измерений

Гироскопом называется симметричное твёрдое тело, быстро вращающееся вокруг одной из главных осей инерции. Чтобы ось гироскопа могла свободно поворачиваться в пространстве, его закрепляют на кольцах так называемого карданова подвеса (рис. 9.1), в котором оси внутреннего уу и внешнего zz колец и ось гироскопа хх пересекаются в одной точке, называемой центром подвеса. Такой гироскоп имеет три степени свободы и может совершать любой поворот около центра подвеса.

Гироскоп характеризуется двумя основными свойствами. Первое свойство гироскопа с тремя степенями свободы состоит в том, что его ось стремится устойчиво сохранять в мировом пространстве приданное ей первоначальное направление. Если эта ось вначале направлена на какую-либо звезду, то при любых перемещениях прибора и случайных толчках она будет продолжать указывать на эту звезду, меняя свою ориентировку относительно осей, связанных с Землёй.

Второе свойство гироскопа обнаруживается, когда на его ось начинает действовать сила, приложенная в точке, не совпадающей с центром масс гироскопа. Казалось бы, что под действием силы 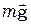ось гироскопа xx должна начать поворачиваться вокруг оси yy, а она начинает поворачиваться вокруг оси zz, т. е. вокруг направления действия силы.Это свойство получило название гироскопического эффекта. Вращение же оси вращения гироскопа вокруг направления действия силы называется прецессией.

Поведение гироскопа, на первый взгляд, противоестественное, полностью объясняется основным законом динамики вращательного движения (см. формулу на с. 22), который в этом случае удобно записать в виде

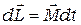. (9.1)

Из (9.1) следует, что внешний момент силы 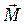за промежуток времени 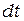вызывает изменение момента импульса 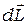, направленное параллельно вектору момента внешней силы 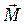. Наглядно представить поведение гироскопа можно с помощью рис. 9.2.

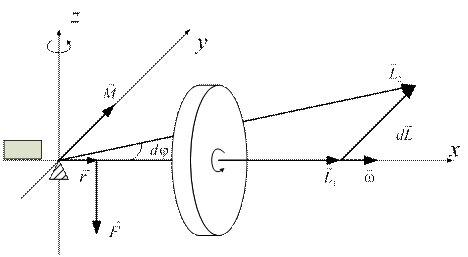
Рис. 9.2

На рис. 9.2 гироскоп вращается вокруг оси x. Следовательно, и его угловая скорость 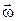, и момент импульса 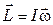направлены вдоль оси x.При действии на ось гироскопа внешней силы, направленной вдоль оси z, возникает момент силы, который, согласно определению момента силы 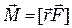, направлен вдоль оси y, перпендикулярно плоскости рисунка. Т. е. вектор 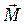перпендикулярен вектору 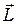, а это значит, что он не может изменить модуль момента импульса, а изменяет только направление вектора .

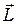Таким образом, конец вектора 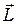, а следовательно, ось вращения гироскопа x, описывает окружность вокруг оси z. Говорят, что ось вращения гироскопа прецессирует вокруг оси z.

Прецессия происходит с постоянной угловой скоростью W. Ее легко измерить на опыте, определив угол 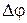, на который поворачивается ось гироскопа за время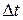

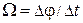. (9.2)

Угловая скорость прецессии связана с величиной внешнего момента силы и угловой скоростью вращения гироскопа. Рассмотрим бесконечно малый промежуток времени dt. Угол, на который ось гироскопа повернётся за это время, также бесконечно мал 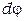, поэтому длина вектора 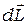практически совпадает с длиной дуги, которую за это время описывает конец вектора .

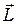Из рис. 9.2 следует, что

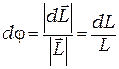, (9.3)

где 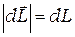– модуль вектора 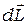, 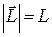– модуль вектора .

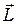C учетом (9.3) и (9.1), формулу (9.2) можно представить в виде

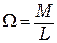. (9.4)

Итак, при постоянной скорости вращения гироскопа 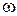скорость прецессии 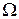прямо пропорциональна модулю момента внешней силы.

В данной работе силой 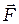, действующей на ось гироскопа, является сила натяжения нити, на которой подвешен груз массой m. В данном случае ее можно считать равной силе тяжести груза 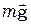. Плечо этой силы 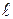есть расстояние от центра карданова подвеса до точки приложения силы, поскольку радиус-вектор точки приложения силы 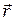и сила 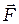взаимно перпендикулярны. Таким образом, модуль момента силы равен .

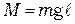Если в (9.4) подставить выражения для модуля момента силы и момента импульса тела, то она примет вид

,

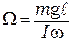откуда скорость вращения гироскопа

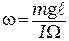. (9.5)

Скорость вращения гироскопа велика для того, чтобы её можно было определить непосредственно, а формула (9.5) позволяет ее легко рассчитать, если известен момент инерции гироскопа.