Описание установки и метода измерений

Вращающееся тело в виде стержня неправильной формы закреплено на оси ОО, проходящей через его центр масс (рис. 8.1). Шарик массой m, свободно падающий с высоты h, ударяется о стержень нарасстоянии r от оси вращения. В результате удара стержень начинает вращаться, а шарик либо отскакивает вверх, либо продолжает движение вниз с изменившейся скоростью. Из-за трения в подшипнике спустя некоторое время t тело останавливается, сделавn оборотов.

При ударе систему "шарик – тело" можно считать замкнутой и поэтому для неё можно записать закон сохранения момента импульса.

Перед ударом тело неподвижно, следовательно, момент импульса системы непосредственно перед ударом 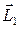равен только моменту импульса шарика, который можно считать точкой,

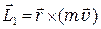, (8.1)

где 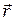– радиус-вектор точки, в которой происходит удар, 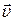– скорость шарика перед ударом.

После удара момент импульса системы 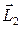складывается из момента импульса шарика и момента импульса вращающегося тела

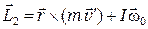, (8.2)

где 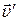– скорость шарика после удара, I – момент инерции тела, 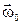– начальная скорость вращения, которую тело приобретает в момент удара.

Итак, закон сохранения момента импульса для системы "шарик – тело" имеет вид

.

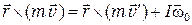В последнем выражении все величины направлены по одной прямой, поэтому в скалярной форме оно выглядит так:

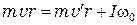. (8.3)

Уравнения (8.3) недостаточно для определения момента инерции тела I. Но если удар считать абсолютно упругим (практически так оно и есть), то для системы "шарик – тело" можно записать закон сохранения механической энергии

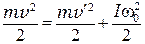, (8.4)

где 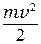и 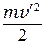– кинетические энергии шарика до и после удара, 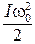– кинетическая энергия тела непосредственно после удара.

Исключив из системы уравнений (8.3) и (8.4) скорость шарика после удара (которую практически невозможно найти), получим формулу для расчета момента инерции тела

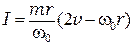. (8.5)

Скорост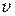и и 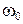легко определить на опыте. Если сопротивлением воздуха пренебречь, то для шарика можно записать закон сохранения механической энергии

,

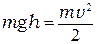откуда . (8.6)

Начальную угловую скорость тела 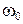находят, руководствуясь следующими соображениями. После удара вращение тела является равнозамедленным, следовательно, описывается уравнениями

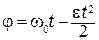
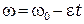, (8.7)

где t – время, в течение которого тело останавливается; 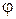– угол, на который оно поворачивается за это время, 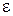– угловое ускорение вращающегося тела; 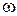– угловая скорость тела в момент времени t.

Поскольку 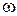= 0, тоиз (8.7) получается

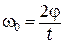. (8.8)

Угол 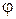можно найти, зная число оборотов n, совершенных телом до остановки. Так как поворот на один оборот соответствует повороту на угол 2p радиан, то 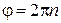, и (8.8) принимает вид

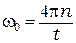. (8.9)

Данные, полученные выше, позволяют, пользуясь основным законом динамики вращательного движения, найти момент силы трения в подшипнике

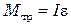. (8.10)

Выразив угловое ускорение из (8.7) и подставив его в (8.10), получают окончательную формулу для расчета момента силы трения в подшипнике

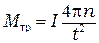. (8.11)