Описание установки и метода измерений

Установка для исследования взаимодействия шаров при ударе (рис. 7.1) состоит из треноги, кронштейнов, к которым через бифилярные подвесы подвешены шары, и градусной шкалы.

В работе до удара движется один шар массой m₁, поэтому закон сохранения импульса имеет вид

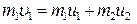. (7.6)

Чтобы проверить выполнение закона сохранения импульса и рассчитать коэффициент восстановления энергии, необходимо знать скорости шаров непосредственно перед ударом и после него. Определение скоростей шаров производится в предположении, что сопротивление воздуха отсутствует и к движению отдельного шара применим закон сохранения механической энергии.

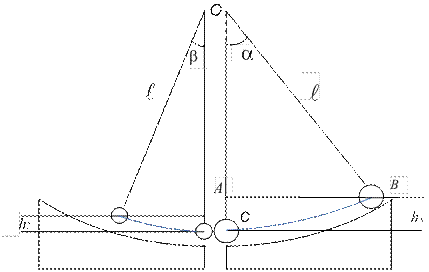
Рис. 7.1

Для сообщения шару m₁ скорости его отклоняют от положения равновесия на угол aи затем отпускают. В наивысшем положении В скорость шара равна нулю, и он обладает только потенциальной энергией, а в наинизшем положении С его высота равна нулю и он обладает только кинетической энергией. Так как сопротивлением воздуха пренебрегают, закон сохранения механической энергии для шара имеет вид

,

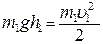откуда

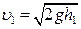, (7.7)

где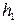– высота, на которую поднимается шар при отклонении на угол a, 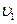– скорость шара непосредственно перед ударом.

Высоту, на которую поднимается центр масс шара при отклонении от положения равновесия, измерить невозможно, но ее можно выразить через угол a. Рассмотрев треугольник АОВ, в котором гипотенуза равна длине подвеса ОВ = 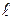,а прилежащий катетАО = 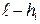, найдем, что

,

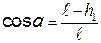откуда

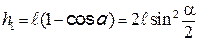. (7.8)

Подставив (7.8) в (7.7), найдем скорость шара перед ударом

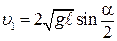. (7.9)

Скорости первого и второго шаров после удара находят также по формуле (7.9), в которой 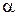меняют соответственно на 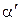– угол отклонения первого шара после удара – и β – угол отклонения второго шара после удара

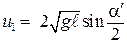, (7.10)

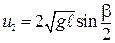. (7.11)

Подставив (7.9), (7.10) и (7.11) в (7.6), получают формулу для проверки закона сохранения импульса в данной работе

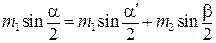. (7.12)

В (7.12) скорость первого шара до удара считают положительной, остальным скоростям приписывают знак в зависимости от направления отклонения шаров.

Подставив (7.9), (7.10) и (7.11) в (7.5), получают формулу для расчета коэффициента восстановления энергии

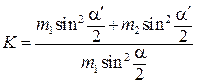. (7.13)