Порядок выполнения работы

1. Определить массу цилиндра взвешиваниемна технических весах (однократное прямое измерение).

2. С помощью штангенциркуля произвести многократные прямые измерения высоты цилиндра и найти ее среднее значение áhñ.

3. С помощью микрометра произвести многократные прямыеизмерения диаметра цилиндра и найти его среднее значениеádñ. Причем следует измерять диаметр разных по высоте цилиндра сечений.

4. Рассчитать среднее значение плотности тела árñ по формуле (0.3), подставив в неё средние значения измеренных величин.

5. Результаты измерений и вычислений занести в таблицу

6. Рассчитать случайные погрешност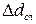и и 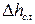по формуле (П.2)

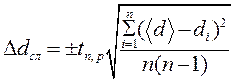и ,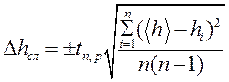

где 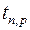– коэффициент Стьюдента, зависящий от числа измерений n и доверительной вероятности р (определяется по таблице коэффициентов Стьюдента).

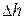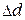7. Рассчитать полные абсолютные погрешности измерений и по формуле (П.3), т. е.

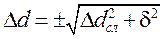и ,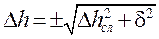

где 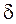– приборные погрешности, которые в данной работе совпадают с

точностью приборов.

8. Рассчитать относительную погрешность плотности 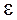по формуле (П.8), т. е.

,

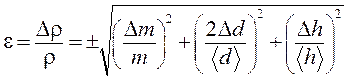где Dm – приборная погрешность весов.

9. Рассчитать абсолютную погрешность измерения плотности по (П.4)

.

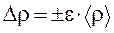10. Записать окончательный результат, в соответствии с (П.11), в виде

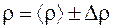
и правильно его округлить.

Контрольные вопросы

1. Что такое плотность вещества? Поясните ее физический смысл. Из какого металла изготовлен Ваш образец?

2. Какие погрешности называются систематическими, какие – случайными?

3. Какие измерения называются прямыми, какие – косвенными?

4. Что характеризует среднее арифметическое измеряемой величины?

5. Что такое доверительный интервал и доверительная вероятность?

6. Как рассчитывается доверительный интервал при прямых измерениях?

7. Чему равна относительная погрешность? Каков ее смысл?

8. Выведите формулу для расчета относительной погрешности в данной

работе.

Литература

1. Денисов И. В., Сырых Л. М. Обработка и представление результатов измерений : учеб. пособие. – Владивосток / ДВГМА, 2000. – 37 с.

Работа 1.1

ИССЛЕДОВАНИЕ ОСНОВНОГО ЗАКОНА ДИНАМИКИ
ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ С ПОМОЩЬЮ
МАЯТНИКА ОБЕРБЕКА

(вариант I – постоянным остается момент инерции)

Цель работы: 1) показать, что при неизменном моменте инерции маятника Обербека отношение момента силы к угловому ускорению 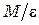остается постоянным; 2) найти момент инерции маятника.

Приборы и принадлежности: маятник Обербека, набор грузов, секундомер, штангенциркуль, масштабная линейка.

Описание установки и метода измерений

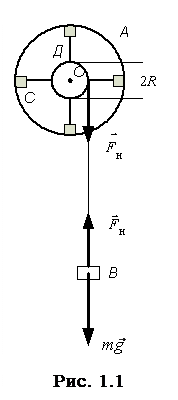
Маятник Обербека (рис. 1.1), с помощью которого производится исследование, состоит из шкива радиуса R, закреплённого на оси О, двух стержней Д, расположенных под углом 90˚ друг к другу, и четырёх одинаковых цилиндрических грузов С, которые можно перемещать вдоль стержней и закреплять на разных расстояниях от оси, а также кольца А. Грузы закрепляются симметрично, так, чтобы центр масс маятника совпадал с осью его вращения. Прибор приводится в движение с помощью груза В массой 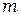, прикреплённого к концу шнура, навитого на шкив.

Основной закон динамики вращательного движения в данной работе удобно записать в виде

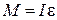, (1.1)

где М – модуль результирующего момента сил, действующего на маятник, I – момент инерции маятника, 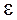– его угловое ускорение.

Из (1.1) следует, что при неизменном моменте инерции угловое ускорение маятника должно изменяться пропорционально результирующему моменту сил. Это значит, во сколько раз изменится момент сил, во столько же раз должно измениться угловое ускорение, т. е. при неизменном моменте инерции

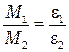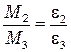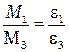, , . (1.2)

Проверка соотношений (1.2) и является целью данной работы.

Результирующий момент сил представляет собой сумму двух моментов: момента 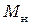, создаваемого силой натяжения нити 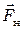, и момента силы трения в подшипниках .

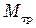Силу натяжения нити 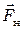легко найти, записав II закон Ньютона для груза В, движущегося поступательно с ускорением :

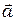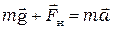. (1.3)

В скалярной форме уравнение (1.3) имеет вид

,

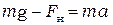откуда 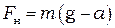. (1.4)

Так как плечо силы натяжения равно радиусу шкива R, то ее момент

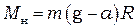. (1.5)

Ускорение груза можно найти с помощью уравнения равноускоренного движения

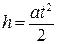, откуда 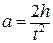, (1.6)

где h – высота падения груза, 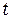– время падения.

Для определения момента силы трения 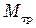пользуются набором гирек массой 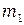от 10 до 50 г. К нити поочередно прикрепляют гирьки и подбирают такую, при которой вращение маятника оказывается равномерным (для того, чтобы маятник начал вращаться, его надо подтолкнуть). Равномерное вращение указывает на то, что момент, созданный гирькой массой 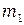, уравновешивает момент силы трения. Таким образом, момент силы трения равен

.

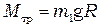Моменты 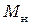и 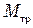имеют противоположные направления, поэтому модуль результирующего момента сил М, действующего на маятник, равен

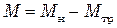. (1.7)

Если окажется, что 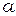<< 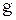,то ускорением 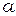в (1.5) можно пренебречь и формулу (1.7) записать в виде

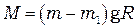. (1.8)

Угловое ускорение маятника Обербека, соответствующее данному вращающему моменту, находят, руководствуясь следующими соображениями. Если нить, на которой подвешен груз m, считать нерастяжимой, то все точки нити и любая точка поверхности шкива имеют то же тангенциальное ускорение, что и груз, следовательно, угловое ускорение маятника

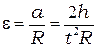. (1.9)