По правилу дифференцирования сложных функций находим
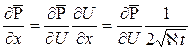 ;
;
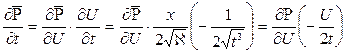 ;
;
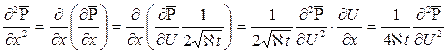 .
.
Подставляя найденные значения производных в уравнение (7.14), получаем обыкновенное дифференциальное уравнение
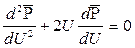 , (7.15)
, (7.15)
которое должно быть проинтегрировано по условиям (7.13)
Для решения (7.15) обозначим 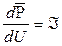 , тогда уравнение (7.15) принимает вид
, тогда уравнение (7.15) принимает вид
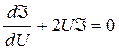 . (7.20)
. (7.20)
Разделяя переменные в (7.20) и интегрируя, получаем
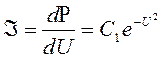 , (7.21)
, (7.21)
где С1 – постоянная интегрирования.
Интегрируя (7.21), будем иметь
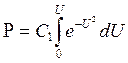 - по первому условию из (7.13).
- по первому условию из (7.13).
Второе условие из (7.13) дает
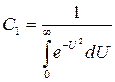 .
.
Из интегрального исчисления известно, что
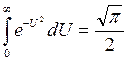 - интеграл Пуассона;
- интеграл Пуассона;
поэтому 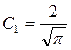 , а
, а 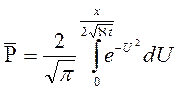 . (7.22)
. (7.22)
Интеграл в (7.22) называется интегралом вероятности и является табулированной функцией, изменяющейся в пределах от 0 до 1:
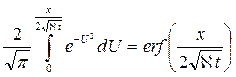 - интеграл вероятности или функция
- интеграл вероятности или функция
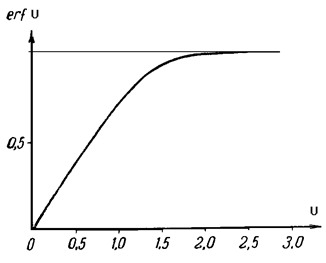 Крампа (график функции представлен на рис.42)
Крампа (график функции представлен на рис.42)
Рис. 42
Таким образом
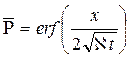 .
.
Тогда закон распределения давления в неустановившемся прямолинейно-параллельном потоке упругой жидкости имеет вид
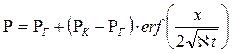 . (7.23)
. (7.23)
Зная х и t, определяем значение 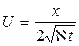 , а затем из таблиц или из графика находим
, а затем из таблиц или из графика находим 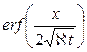 и находим по формуле (7.23) значение давления Р.
и находим по формуле (7.23) значение давления Р.
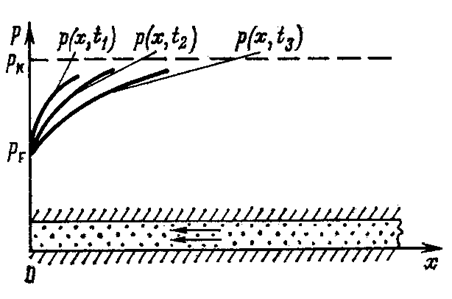 |
Распределение давления Р(х,t) показано на рис.43.
Рис. 43
Найдем дебит Q галереи.
Будем считать положительным дебит, отбираемый из галереи (х=0), когда поток движется против оси х.
Согласно закону Дарси, имеем
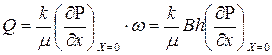 ,
,
где В, h – соответственно ширина и толщина пласта.
Дифференцируя выражение (7.23), получаем
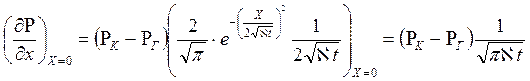 .
.
Дата добавления: 2016-11-04; просмотров: 1477;











