Распределение энергии в спектре АЧТ.
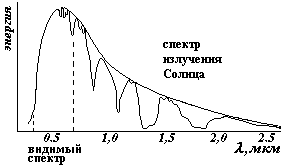
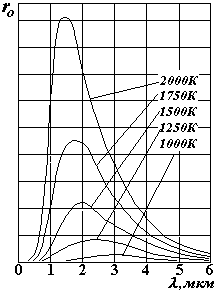 На рисунке приведена зависимость излучательной способности АЧТ от длины волны при различных температурах. Эти данные получены экспериментально. Из графиков видно, что энергия распределяется по длинам волн неравномерно, с увеличением температуры излучение резко возрастает. При указанных температурах максимумы излучения попадают в инфракрасный диапазон длин волн, на видимую область (0,4-0,75 мкм) приходится незначительное количество энергии . С ростом температуры максимумы смещаются в сторону более коротких длин волн. На втором рисунке приведен для сравнения спектр солнечного излучения. «Провалы» в спектре – это линии поглощения атмосферой, огибающая – спектр излучения АЧТ.
На рисунке приведена зависимость излучательной способности АЧТ от длины волны при различных температурах. Эти данные получены экспериментально. Из графиков видно, что энергия распределяется по длинам волн неравномерно, с увеличением температуры излучение резко возрастает. При указанных температурах максимумы излучения попадают в инфракрасный диапазон длин волн, на видимую область (0,4-0,75 мкм) приходится незначительное количество энергии . С ростом температуры максимумы смещаются в сторону более коротких длин волн. На втором рисунке приведен для сравнения спектр солнечного излучения. «Провалы» в спектре – это линии поглощения атмосферой, огибающая – спектр излучения АЧТ.
Законы изучения АЧТ. На основании экспериментальных данных были получены следующие законы:
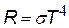
| Закон Стефана-Больцмана «Энергетическая светимость АЧТ прямо пропорциональна четвертой степени абсолютной температуры». Из закона следует, что при небольшом увеличении температуры, энергия излучения возрастает очень сильно. Например, при увеличении температуры в 2 раза, излучаемая энергия возрастает в 16 раз. s = 5,67×10-8 Вт/(м2К4) – постоянная Стефана-Больцмана. |
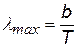
| Закон смещения Вина: «Длина волны, на которую приходится максимум излучения, обратно пропорциональна абсолютной температуре». Из закона следует, что с увеличением температуры максимум излучения смещается в сторону более коротких волн. b= 2,9×10-3 1/м – постоянная Вина. |
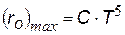
| Закон общепринятого названия не имеет, иногда называется 2-ым законом Вина: «Максимальная излучательная способность прямо пропорциональна пятой степени абсолютной температуры» С = 1,3×10-5 Вт/(м3.К5)- коэффициент пропорциональности |
Выясним, что представляют собой величины в формулах (§) и (§§) на графике зависимости излучательной способности АЧТ ro от длины волны l.
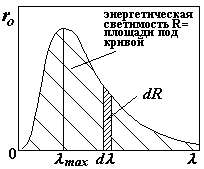
| Кривая излучения АЧТ. dR – поток излучения, приходящийся на интервал длин волн dl (площадь плотно заштрихованной полоски) R – интеграл (см. формулу §§) – на графике – это площадь под всей кривой излучения. lmax – длина волны, на которую приходится максимум излучения |
Гипотеза и формула Планка.
Все попытки получить формулу, описывающую кривую излучения АЧТ оказались безуспешными. Две из полученных формул (формула Вина и формула Релея и Джинса) достаточно хорошо подходили при малых и при больших длинах волн, но полностью описать кривую не могли (см. таблицу ниже). Получить формулу, полностью описывающую кривую излучения АЧТ удалось Планку. Он впервые выдвинул квантовую гипотезу(1900 г)о том, что свет испускается порциями – квантами. Энергия одного кванта пропорциональна частоте излучения. Это была принципиально новая гипотеза, положившая начало развитию квантовой теории.
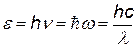
| энергия кванта (фотона), выраженная через частоту n (Гц), циклическую частоту w (1/с)и длину волны l |
h = 6,625×10-34 Дж.с - постоянная Планка
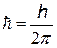 = 1,05×10-34 Дж.с = 1,05×10-34 Дж.с 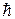 - называют квантом действия
(в устной речи произносится «аш перечеркнутая - называют квантом действия
(в устной речи произносится «аш перечеркнутая
|
Мы не будем приводить вывод формулы Планка , укажем только, что он основан на методах статистической термодинамики, как и вывод формул Вина и Релея-Джинса, но Планк предположил, что энергия, приходящаяся на одну степень свободы колебательного движения осциллятора равна не кТ/2, а зависит от частоты излучения.
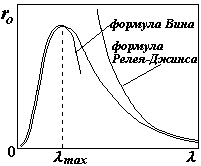 Приближенная формула Вина хорошо выполняется при малых длинах волн (см. рис.) и дает максимум; формула Релея - Джинса дает неплохое совпадение с опытом при больших длинах волн, но кривая уходит в бесконечность, что физически невозможно. (Подробнее – см. таблицу ниже)
Приближенная формула Вина хорошо выполняется при малых длинах волн (см. рис.) и дает максимум; формула Релея - Джинса дает неплохое совпадение с опытом при больших длинах волн, но кривая уходит в бесконечность, что физически невозможно. (Подробнее – см. таблицу ниже)
| Название | выражение через частоту n | выражение через длину волны l |
| формула Планка | 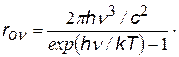 ª ª
| 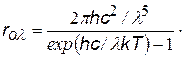 ªª ªª
|
| формула Вина, хорошо выполняется при hn>> kT или l£ lmax = b/T b = 0,0029 м.К (см.ранее закон смещения Вина | 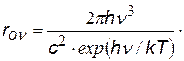
| 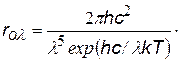
|
| формула Релея - Джинса хорошо выполняется при hn << kT или l >> l max = b/T (ех » 1+ х при малых х) | 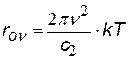
| 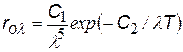 С1 » 3,7×10-16 Вт.м2
С2»1,4×10-2 м.К
С1 » 3,7×10-16 Вт.м2
С2»1,4×10-2 м.К
|
Из формулы Планка можно получить теоретически все законы излучения АЧТ.
| Чтобы получить закон Стефана-Больцмана, нужно просуммировать излучение по всем частотам | Подставим под интеграл (ª), сделаем замену переменной. Интеграл получается не табличный, но известен из математики; А = const, в которой собраны все постоянные, входящие в формулу Планка |
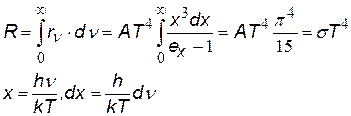
| |
| Чтобы получить закон смещения Вина, нужно приравнять первую производную излучательной способности нулю, что будет соответствовать максимуму излучения drol / dl = 0. Возьмем формулу (ªª), найдем производную, получим уравнение. Введем переменную x =hc / kTl подставим в уравнение | В результате получим: 5(ex – 1) -xex = 0 Это уравнение можно решить только численно: х» 5. Подставляя, найдем: l = const/T |
Законы теплового излучения используются в приборах, с помощью которых измеряют бесконтактным способом температуру тел, нагретых до высоких температур. Такие приборы называются пирометрами. Шкала такого прибора заранее проградуирована. С помощью оптических линз изображение источника излучения (например, отверстия печи, лампочки накаливания) фокусируется на датчике прибора, и стрелка указывает температуру на шкале прибора.
ДУАЛИЗМ СВОЙСТВ ЭЛЕКТРОМАГНИТНОГО ИЗЛУЧЕНИЯ
Прежде, чем перейти к закономерностям фотоэффекта и эффекта Комптона, рассмотрим свойства света (электромагнитного излучения). В одних явлениях (интерференция, дифракция, поляризация) свет проявляется себя как волны, в других (тепловое излучение, фотоэффект, эффект Комптона) – как частицы (кванты, фотоны), поэтому говорят о двойственной, корпускулярно волновой природе света. Если частота света и, следовательно, энергия фотона, велика, то свет проявляется себя как «частицы», при малых частотах – как волны. Например, в области радиоволн квантовые свойства практически не проявляются, и волновая электромагнитная теория хорошо объясняет явления, связанные с радиоволнами.
В силу двойственности природы света, для его характеристики используются как квантовые, так и волновые величины.
Свет как фотоны (кванты) характеризуется:
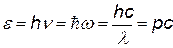
| энергия фотона |
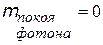
| масса покоя фотона равна 0. Действительно, энергия частицы по формуле Эйнштейна 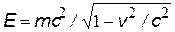 , скорость света (и фотона) в вакууме равна с, следовательно, m = 0 , скорость света (и фотона) в вакууме равна с, следовательно, m = 0
|
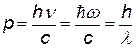
| импульс фотона. Действительно, из СТО энергия частицы связана с ее импульсом 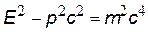 ,m=0 Þ hn = pc ,m=0 Þ hn = pc
|
Свет как электромагнитные волны характеризуются:
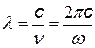 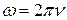
| l- длина волны, n - частота (в Гц), w - циклическая частота, с – скорость света в вакууме |
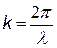 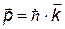
| k в скалярной форме называют волновым числом, в векторной форме называют волновым вектором р – импульс фотона |
| В атомной физике энергию обычно измеряют не в джоулях, а в электронвольтах (эВ). 1 эВ = 1,6×10-19 Дж. Электронвольт численно равен той энергии, которую приобретает электрон, пройдя разность потенциалов в 1 вольт. Электронвольты и вольты численно совпадают, хотя этими единицами измеряются совершенно разные величины. Например, электрон пройдя разность потенциалов 5 В приобретает энергию 5 эВ. |
В нашем мире мы не наблюдаем таких макрообъектов, которые проявляли бы себя то как частицы, то как волны. Поэтому все попытки представить себе, что же такое свет, оказались безуспешными. Фотоны не подчиняются законам классической механики. Двусмысленность природы света возникает потому, что мы используем классические представления для описания неклассических, квантовых объектов.
ФОТОЭФФЕКТ
Фотоэффектом называют электрические явления, происходящие под действием электромагнитного излучения (света). Различают следующие виды фотоэффекта.
1)Внешний фотоэффект. Он состоит в том, что под действием света происходит
испускание электронов из вещества (см. рис.). При этом на поверхности
вещества появляется положительный заряд.
2)Внутренний фотоэффект. Выбитые светом электроны остаются в веществе.
Если к веществу приложена разность потенциалов, то при освещении светом
электропроводность вещества увеличивается.
3)Фотоэффект в запирающем слое (вентильный фотоэффект). Если привести в контакт два вещества с разным типом проводимости (электронной и дырочной), то на их границе возникает разность потенциалов. Если освещать границу контакта светом и цепь замкнуть, то в ней будет протекать ток. Таким образом, можно наблюдать непосредственное преобразование световой энергии в электрическую (подробнее см.дальше - ФТТ)
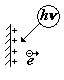 внешний фотоэффект
внешний фотоэффект
|  внутренний фотоэффект
внутренний фотоэффект
| 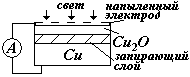 фотоэффект в запирающем
слое
фотоэффект в запирающем
слое
|
Мы будем рассматривать только внешний фотоэффект. Попытки объяснить закономерности фотоэффекта на основе электромагнитной теории оказались невозможными, например, из теории следовало, что появление фототока должно происходить спустя десятки минут после освещения, тогда как из опыта фототок появлялся практически мгновенно. В 1905 г Эйнштейн показал, что закономерности внешнего фотоэффекта можно объяснить, если предположить, что свет поглощается порциями (квантами) такими же, как по предположению Планка свет излучается. Он предложил уравнение:
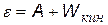 © ©
| уравнение Эйнштейна для внешнего фотоэффекта |
По сути – это закон сохранения энергии: энергия фотона e расходуется на работу А по отрыву электрона от атома и на сообщение электрону кинетической энергии Wкин . (На свободном, не связанном с атомом электроне, фотоэффект невозможен).
Фотоэффект можно рассматривать как неупругое столкновение частицы-фотона с атомом; фотон исчезает, из атома вылетает электрон, и часть импульса «погибшего» фотона передается атому.
Для удобства решения задач соберем все выражения для величин в формуле
(©) в таблицу. В зависимости от условия задачи, следует выбрать подходящие
формулы и подставить в (©).
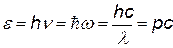
| энергия падающего фотона | ||
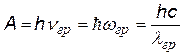
| А – работа выхода электрона из вещества | ||
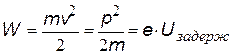
| максимальная кинетическая энергия электрона. Uзадерж- задерживающий потенциал (см.дальше), е – заряд электрона, р – импульс электрона | ||
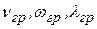
| все эти величины называются красной границей фотоэффекта. Красная граница фотоэффекта – это частота или длина волны, при которых начинается (или прекращается) фотоэффект | 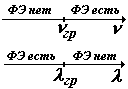
| |
| W, v, p | Кинетическая энергия, скорость и импульс в формуле Эйнштейна являются максимальными, т.е. электрон имеет их сразу же после отрыва от атома. «Пробираясь к выходу» из вещества за счет взаимодействия с другими частицами, он может потерять энергию, поэтому вылетевшие электроны имеют различные скорости (вплоть до 0). | ||
| Uзадерж | задерживающее напряжение (потенциал) – это обратное напряжение, которое нужно приложить между катодом и анодом фотоэлемента, чтобы прекратился фототок (см. рис. ниже) | ||
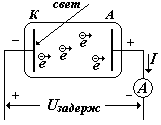 Рассмотрим вакуумный фотоэлементи его характеристики.1)Вольтамперная характеристика.
Рассмотрим вакуумный фотоэлементи его характеристики.1)Вольтамперная характеристика.
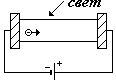
На рисунке показана схема, используемая для изучения фотоэффекта. Внутри стеклянного баллона, из которого откачен воздух, имеются два электрода: катод (К) и анод (А). Такое устройство называется вакуумным фотоэлементом. При освещении катода светом, из него будут вылетать электроны, образуя электронное облако. Часть электронов по инерции достигнут анода. Если катод и анод замкнуть вне баллона и подсоединить микроамперметр, то прибор покажет ток.
Этот очень небольшой ток называется инерционным (Iин).
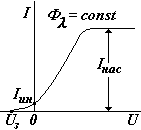 Если к электродам подсоединить батарею и увеличивать напряжение между катодом и анодом, ток в цепи будет увеличиваться. Зависимость фототока от напряжения называется вольтамперной характеристикой фотоэлемента ( см. рис.). Начиная с некоторых напряжений, ток перестает увеличиваться, если при этом световой поток
Если к электродам подсоединить батарею и увеличивать напряжение между катодом и анодом, ток в цепи будет увеличиваться. Зависимость фототока от напряжения называется вольтамперной характеристикой фотоэлемента ( см. рис.). Начиная с некоторых напряжений, ток перестает увеличиваться, если при этом световой поток
Ф остается постоянным. Максимальный ток называется током насыщения (Iнас). Существование тока насыщения объясняется следующим образом. Один фотон выбивает только один электрон, но не каждый фотон выбивает по электрону. Отношение числа выбитых электронов Nэл к числу падающих фотонов Nфот в единицу времени называется квантовым выходом. Квантовый выход a зависит от природы вещества и частоты фотонов.
Дата добавления: 2021-02-19; просмотров: 604;











