Установившееся движение газированной жидкости
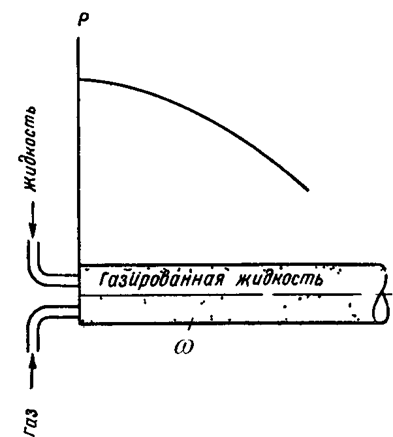 |
Рассмотрим установившееся движение газированной жидкости, которое имеет место в пористой среде, когда залежь разрабатывается при пластовом давлении ниже давления насыщения. В этом случае растворенный газ выделяется из нефти и происходит движение двух фаз: нефти и свободного газа. Теория движения газированной жидкости была разработана значительно раньше теории Баклея-Леверетта. Первые гидродинамические исследования о движении газированной жидкости в пористой среде принадлежат Л.С.Лейбензону, а первые эксперименты по определению фазовых проницаемостей для жидкости и газа были выполнены Викофом и Ботсетом еще в 1936 г.
Рис. 70
Рассмотрим стационарное прямолинейное движение газированной жидкости в пористой среде, заполняющей трубу постоянного сечения w (рис.70). предполагается, что фильтрация каждой из фаз подчиняется закону Дарси, т.е.
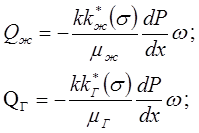 (10.29)
(10.29)
где mж, mг – соответственно вязкость жидкости и газа, которые считаются постоянными (т.е. не зависимыми от давления Р);
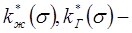 относительные фазовые проницаемости соответственно для жидкости и газа;
относительные фазовые проницаемости соответственно для жидкости и газа;
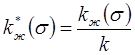 ;
; 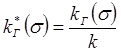 . (10.30)
. (10.30)
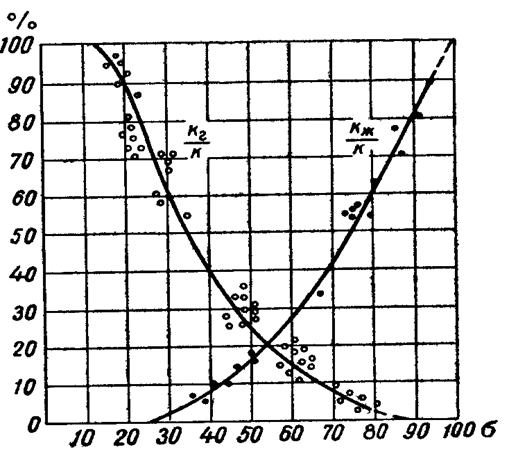
Характер кривых относительных фазовых проницаемостей 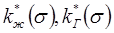 , полученных экспериментально, показан на рис.71.
, полученных экспериментально, показан на рис.71.
Рис. 71
Отмечаются характерные особенности кривых:
1) при малом количестве газа (высокая насыщенность s жидкостью) проницаемость 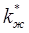 < 1, т.е. незначительное количество свободного газа весьма сильно уменьшает проницаемость жидкости
< 1, т.е. незначительное количество свободного газа весьма сильно уменьшает проницаемость жидкости 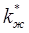 , и, следовательно, дебит жидкости Qж . Поэтому стараются не допускать чрезмерного выделения газа на забоях скважин, чтобы не снизить фазовую проницаемость жидкости
, и, следовательно, дебит жидкости Qж . Поэтому стараются не допускать чрезмерного выделения газа на забоях скважин, чтобы не снизить фазовую проницаемость жидкости 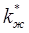 ;
;
2) напротив, жидкость гораздо меньше мешает двигаться газу, чем газ жидкости, т.к. при малых s 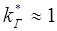 , т.е. при малых насыщенностях жидкостью
, т.е. при малых насыщенностях жидкостью 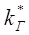 снижается очень мало.
снижается очень мало.
Найдем суммарное количество газа (свободного и растворенного) и приведем это объемное количество газа к атмосферному давлению.
Дебит жидкости Qж содержит объем растворенного газа Qгр, который после приведения к атмосферному давлению можно выразить уравнением:
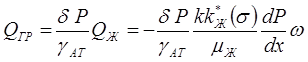 , (10.31)
, (10.31)
где d - коэффициент растворимости газа в жидкости.
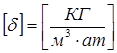 - весовое количество газа, которое растворяется в единице объема жидкости при повышении давления на 1ат;
- весовое количество газа, которое растворяется в единице объема жидкости при повышении давления на 1ат;
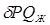 - вес растворенного газа;
- вес растворенного газа;
Р – абсолютное давление.
Находим дебит свободного газа, приведенный к атмосферному давлению. На основании (10.29).
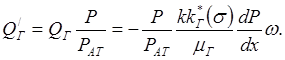 (10.32)
(10.32)
Тогда полный объемный расход газа (QГ)ат на устье скважины при снижении давления до значения атмосферного Рат будет определяться суммой:
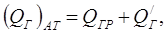
или с учетом (10.31) и (10.32):
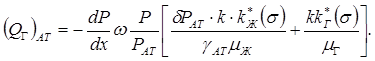 (10.33)
(10.33)
Определим газовый фактор Г, который представляет собой отношение дебита газа, приведенного к атмосферным условиям, к дебиту жидкости, т.е.
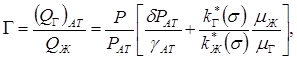
или
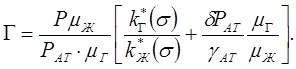 (10.34)
(10.34)
Введем следующие обозначения:
|
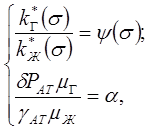
a- величина безразмерная.
Тогда выражение для газового фактора (10.34) можно записать в виде:
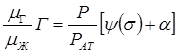 . (10.37)
. (10.37)
Будем рассматривать установившееся движение; при этом всюду в пласте газовый фактор будет одинаков, т.е. Г=const.
Обозначим:
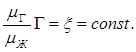 (10.38)
(10.38)
Тогда из (10.37):
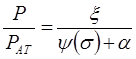 .
.
Обозначим:
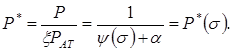 (10.39)
(10.39)
Имея экспериментальные кривые 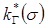 и
и 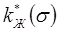 (рис. 71), по формуле (10.35) можно построить зависимость
(рис. 71), по формуле (10.35) можно построить зависимость 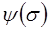 (рис.72). С помощью этой кривой и формулы (10.39) строится графическая зависимость
(рис.72). С помощью этой кривой и формулы (10.39) строится графическая зависимость 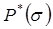 (рис. 73). Затем для фиксированных значений s и экспериментальных кривых (рис. 71) находим
(рис. 73). Затем для фиксированных значений s и экспериментальных кривых (рис. 71) находим 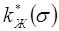 , а из графика (рис.73) определяем соответствующие значения
, а из графика (рис.73) определяем соответствующие значения 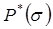 и строим зависимость
и строим зависимость 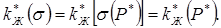 (рис. 74). Таким образом мы пришли к однозначной зависимости относительной фазовой проницаемости от безразмерного давления
(рис. 74). Таким образом мы пришли к однозначной зависимости относительной фазовой проницаемости от безразмерного давления 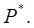
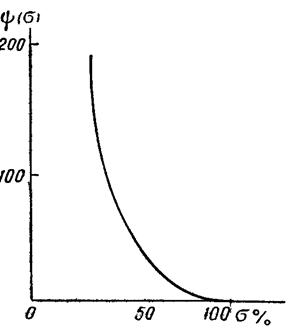
Рис. 72
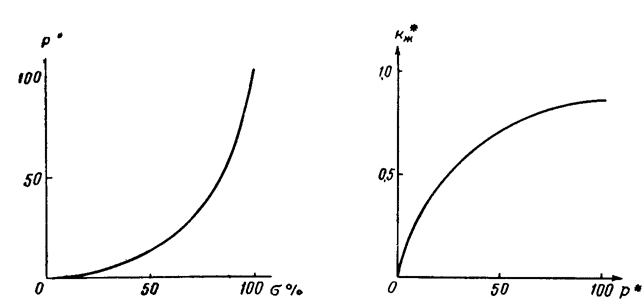
Рис. 73 Рис. 74
Теперь, когда установлена однозначная зависимость 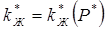 , введем функцию Христиановича:
, введем функцию Христиановича:
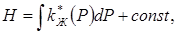 (10.40)
(10.40)
полный дифференциал которой будет:
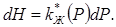 (10.41)
(10.41)
Тогда расход жидкости QЖ по формуле (10.29) можно записать более просто:
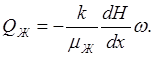 (10.42)
(10.42)
Уравнение (10.42) ничем не отличается от обычного закона Дарси, но только роль давления P играет функция Христиановича Н.
Вычислим функцию Христиановича.
Из формулы (10.39) имеем:
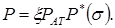 (10.43)
(10.43)
Тогда 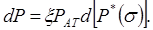
Подставляем выражение dP в (10.41):
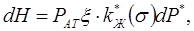
или 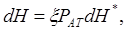 (10.44)
(10.44)
где 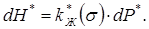 (10.45)
(10.45)
Интегрируем (10.44) и (10.45), получаем:
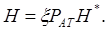 (10.46)
(10.46)
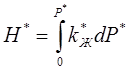 - безразмерная функция (10.47)
- безразмерная функция (10.47)
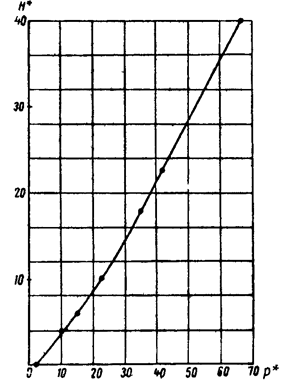
Зависимость 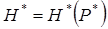 строится по графику (рис. 74) графическим интегрированием по уравнению (10.47). Эта зависимость была впервые построена Б.Б. Лапуком и имеет вид, показанный на рис. 75.
строится по графику (рис. 74) графическим интегрированием по уравнению (10.47). Эта зависимость была впервые построена Б.Б. Лапуком и имеет вид, показанный на рис. 75.
Таким образом, получаем возможность использовать при расчетах стационарного движения газированной нефти все формулы для движения однородной несжимаемой жидкости, в которых давление P должно быть заменено функцией Христиановича Н.
Пользуясь функцией Христиановича (10.46) можно, например, записать выражение для дебита жидкости QЖ из скважины, находящейся в центре кругового пласта, по формуле Дюпюи:
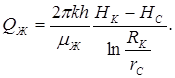
Функция Н здесь будет распределена так же, как давление при фильтрации однородной несжимаемой жидкости: для плоско-радиального движения - по закону логарифмической кривой, для прямолинейно-параллельного движения – по линейному закону.
Последовательность расчетов через функцию Христиановича такова: зная контурные давления РС, РК и газовый фактор Г, по формуле (10.39) находят 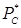 и
и 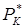 и затем из графика (рис. 75) находят
и затем из графика (рис. 75) находят 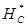 и
и 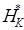 . Зная
. Зная 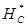 и
и 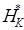 из уравнения (10.46) находят НС и НК, после чего все элементы движения находятся без затруднений.
из уравнения (10.46) находят НС и НК, после чего все элементы движения находятся без затруднений.
Полученную таким образом довольно трудоемкую методику расчетов можно значительно упростить, если учесть, что в широком диапазоне зависимость 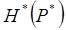 согласно графику (рис. 75) изображается почти прямой линией. Поэтому с достаточной точностью можно принять:
согласно графику (рис. 75) изображается почти прямой линией. Поэтому с достаточной точностью можно принять:
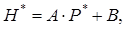 (10.48)
(10.48)
где А и В – постоянные.
 Тогда разность (НК-НС), входящую во все выражения, можно выразить через разность давлений (РК-РС). Действительно, согласно уравнению (10.48), имеем:
Тогда разность (НК-НС), входящую во все выражения, можно выразить через разность давлений (РК-РС). Действительно, согласно уравнению (10.48), имеем:
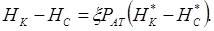
Учитывая (10.48), получаем:
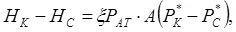
или , учитывая (10.43), имеем:
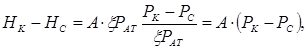
т.е. 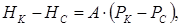 (10.49)
(10.49)
Рис. 75
Значение углового коэффициента А в формуле (10.48), определяемого по графику (рис. 75), равно 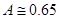 .
.
Таким образом, формула (10.49) показывает, что для приближенных расчетов газированную жидкость можно рассматривать как фиктивную однородную несжимаемую жидкость, движущуюся в пласте, в котором параметр 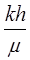 следует заменить величиной
следует заменить величиной 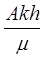 .
.
В развитии этого метода М.М. Глоговским и М.Д. Розенбергом установлено, что параметр А в довольно широких пределах удовлетворительно записывается формулой:
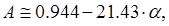 (10.50)
(10.50)
где a определяется выражением (10.36), при этом предполагается условие:
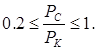
Приложение.
 |
Задачи неустановившегося движения газированной жидкости являются наиболее сложными. Используя метод последовательной смены стационарных состояний (ПССС), К.А. Царевич решил задачу об истощении залежи при режиме растворенного газа. Замкнутый резервуар вскрывался скважиной и начинался отбор жидкости. При этом начальное пластовое давление принималось равным давлению насыщения. Исследуя вторую фазу нестационарного движения – фазу истощения (с момента, когда воронка депрессии достигла границы резервуара), К.А. Царевич пришел к выводу, что за счет энергии растворенного газа можно отобрать лишь около 30% всего запаса, что наглядно представляется графической зависимостью среднего пластового давления от насыщенности
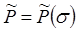 (рис. 76). Из рис. 76 видно, что давление
(рис. 76). Из рис. 76 видно, что давление 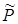 упало до 0, а насыщенность
упало до 0, а насыщенность 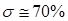 .
.
Рис. 76
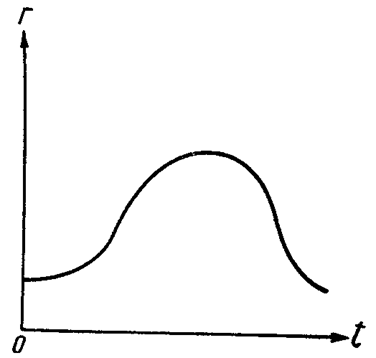 |
Была также исследована задача об изменении газового фактора во времени (рис. 77).
Рис. 77
Установлено, что величина газового фактора вначале растет, достигая некоторого максимума, а затем резко падает.
Первая фаза нестационарного движения газированной жидкости была рассмотрена в работах М.М. Глоговского и М.Д. Розенберга. Было установлено, что первая задача не играет существенной роли по сравнению со всем периодом эксплуатации залежи. Им же исследовалась задача о вытеснении газированной жидкости водой. Для первой фазы решение является сложным и громоздким. Во второй фазе, когда началось вытеснение, газированную жидкость можно заменить фиктивной однородной жидкостью, как отмечалось выше.
Дата добавления: 2016-11-04; просмотров: 3731;











