Теория Баклея-Леверетта

Баклей и Леверетт рассмотрели двухфазную фильтрацию, пренебрегая капиллярным давлением и массовыми силами, для одномерного прямолинейного движения несжимаемой смеси для случая 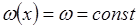. Тогда система (10.8) и уравнения (10.7) принимают вид:

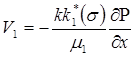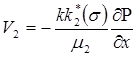; ; (10.12)

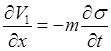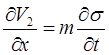; ; (10.13)

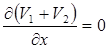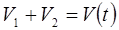; . (10.14)

Здесь V₁ и V₂ – скорости фильтрации соответственно первой (вытесняющей) и второй (вытесняемой) фаз (жидкостей).

Предположим, что суммарный расход жидкостей 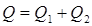постоянный, тогда при 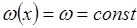имеем

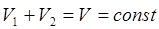. (10.15)

В соответствии с этим из уравнений (10.12) и (10.14) находим

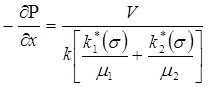. (10.16)

Подставляя выражение (10.16) в первое уравнение (10.12), получаем

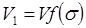, (10.17)

где 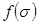- так называемая функция Баклея-Леверетта:

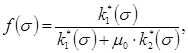
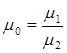. (10.18)

Дифференцируем (10.17) по х и подставляем полученный результат в первое уравнение неразрывности (10.13), получаем

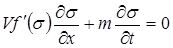. (10.19)

Уравнение (10.19) есть квазилинейное дифференциальное уравнение первого порядка в частных производных, которое обычно интегрируется методом характеристик.

Выпишем систему обыкновенных дифференциальных уравнений, соответствующую уравнению (10.19):

.

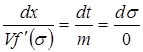Независимая система ее первых интегралов есть:

; .

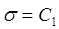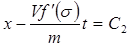Отсюда следует, что при t = 0 расстояние 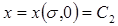- начальное распределение насыщенности. Тогда решением уравнения (10.19) будет

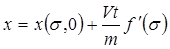. (10.20)

Таким образом с помою решения (10.20), зная положение точки с насыщенностью s в момент t = 0, можно определить ее положение в любой момент времени t > 0.

Дифференцируя (10.20) по времени t, находим

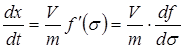. (10.21)

Нетрудно заметить, что выражение (10.21) представляет собой скорость распространения насыщенности заданной величины s.

Вид кривых 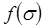и 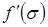, построенных по формуле (10.18) с помощью графиков (рис.64), представлен на рис.65.

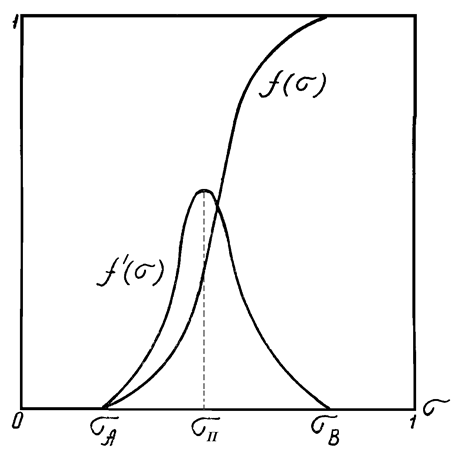Рис.65

Физической особенностью модели Баклея-Леверетта для двухфазной фильтрации является зависимость скорости 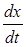распространения того или иного значения насыщенности s от величины этой насыщенности. Это явление называется дисперсией волн. Действительно, в выражении (10.21) в ее правой части 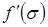зависит от s. Эта зависимость изображена на рис.65, из которого видно, что при значениях насыщенности 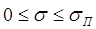( 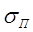- насыщенность, соответствующая точке перегиба графика функции 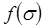) большие значения насыщенности s распространяются с большими скоростями ( 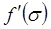возрастает), а при 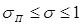наоборот – большие значения насыщенности s распространяются с меньшими скоростями ( 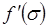убывает). Поэтому, имея начальное распределение насыщенности 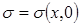, представленное на рис.66, с течением времени профиль распределения насыщенности 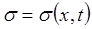довольно резко изменяется, поскольку большие значения насыщенности s «догоняют» меньшие ее значения. Происходит в конечном итоге «опрокидывание» волны насыщенности и возникает неоднозначность в распределении 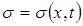: одному и тому же значению х соответствуют три значения насыщенности - 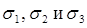, что физически абсурдно, так как в каждом сечении пласта в каждый момент времени может существовать только одна вполне определенная насыщенность s. Такая неоднозначность и устраняется введением скачка насыщенности (линия 1-3-5) из условия равенства площадей сегментов (1-2-3) и (3-4-5). Заметим дополнительно, что возникновение (зарождение) скачка насыщенности происходит в момент t^* , когда касательная к кривой 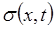стано
вится вертикальной.

Рис.66

Вполне очевидно, что скачок насыщенности представляет собой понятие математическое, не имеющее место в реальных условиях. В действительности же существует конечная длина d (рис.67), где значение насыщенности падает от σ_ф до нуля перед фронтом вытеснения. Размер этой зоны (d) зависит от капиллярных свойств среды и по сравнению с «переходной зоной» – зоной смеси (1+2) очень мал; поэтому в расчетах этой зоной часто пренебрегают (d = 0) и рассматривают лишь переходную зону.

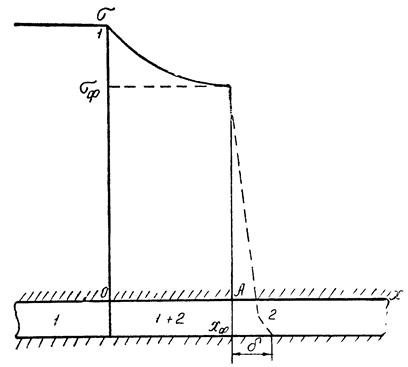
Рис.67

Пусть жидкость 1 вытесняет жидкость 2 (рис.67). Объем первой фазы в начальный момент (t = 0) при 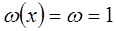запишется интегралом (в переходной зоне ОА)

,

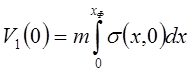где 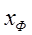- координата фронта или скачка.

В момент времени t объем первой фазы (вторгшейся воды) в этой зоне будет

.

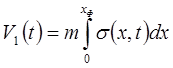За время t через границу х = 0, очевидно, войдет объемное количество жидкости Vt, равное

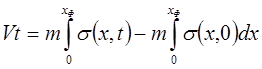. (10.22)

Для простоты принимаем насыщенность нефтью переходной зоны в начальный момент (t = 0) равной 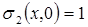, что равнозначно 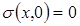; из (10.22) получаем

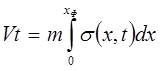, (10.23)

а из (10.20) следует, что

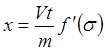, (10.24)

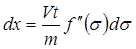. (10.25)