Основы теории конусообразования; предельный безводный и безгазовый дебит скважины

В пологозалегающих пластах с очень малым углом наклона к горизонту площадь водонефтяного контакта очень велика, а поэтому с самого начала эксплуатации скважины оказываются в нефтяном пласте с подошвенной водой. При отборе нефти поверхность водонефтяного контакта деформируется и принимает вид холма. Такой водонефтяной холм называется конусом подошвенной воды. Если повысить депрессию и отбор нефти, то вода прорвется в скважину и скважина будет давать нефть вместе с водой.

Точной теории конусообразования не существует ввиду сложности решения самой математической задачи в ее строгой постановке. Приближенная теория этого явления, выдвинутая Маскетом-Чарным, позволяющая рассчитать предельный безводный дебит и депрессию, исходит из допущения, что отклонение поверхности раздела двух фаз от первоначальной плоской формы не влияет на распределение потенциала скоростей фильтрации в нефтяной части пласта.

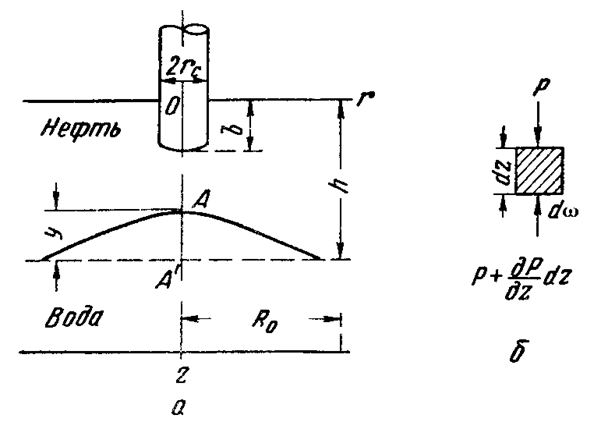Рассмотрим задачу о притоке нефти к скважине, несовершенной по степени вскрытия, но совершенной по характеру вскрытия в изотропном пласте при устойчивом неподвижном конусе подошвенной воды. Движение считаем следующим закону Дарси; кровля, подошва и первоначальная поверхность раздела принимаются горизонтальными. Режим пласта водонапорный; действием капиллярных сил пренебрегаем. (рис. 61).

Рис.61

Прежде всего выясним условия, при которых частицы воды на поверхности конуса будут неподвижными. Предположим, что распределение давления в любой точке пласта известно, т.е. известна функция Р=Р(r,z). (давление как таковое, а не приведенное). Выделим на вершине конуса (r=0) элементарный объем жидкости (цилиндрик) площадью сечения dw, высотой dz и рассмотрим действующие на него силы (полагая, что этот объем попал в нефтяную часть). Давление на верхнюю грань Р=Р(0;z); давление на нижнюю грань Р^/=Р(0;z+dz)=P+dP=P+ 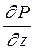dz.

Составим уравнение равновесия сил, действующих на нашу частицу (элементарный объем) воды. Сила, действующая на частицу вверх, будет равна:

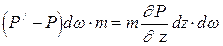, где m- коэффициент пористости.

Сила, действующая на частицу вниз (сила тяжести): 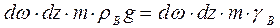; где 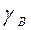-объемный вес воды.

Условие устойчивости элементарного объема воды будет иметь вид

,

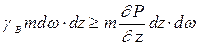или 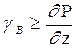. (9.42)

Переходя от давления к потенциалу

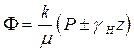, (9.43)

получаем условие устойчивости (9.42) в виде

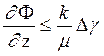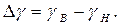, (9.44)

Выясним как распределяется потенциал вдоль границы раздела. Согласно формуле (9.43) потенциал вдоль границы раздела равен

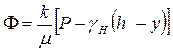. (9.45)

Условие статического равновесия границы раздела (т. А) выражается формулой

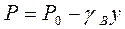, (9.46)

где .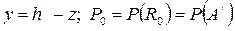

Подставляя значения из (9.46) в (9.45) и замечая, что

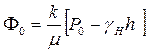(9.47)

есть потенциал на контуре питания R₀ при z=h, получаем окончательно

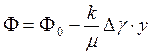, (9.48)

т.е. вдоль границы раздела текущей нефти и неподвижной воды потенциал изменяется линейно. Распределение потенциала вдоль границы раздела текущей нефти - неподвижной воды, вдоль оси скважины и цилиндрической поверхности R₀ , представлен на рис. 62.

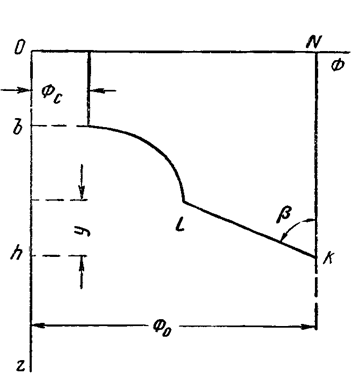
Рис.62

Анализируя распределение потенциала вдоль стенки несовершенной скважины и вдоль оси z невскрытой части пласта при невозмущенном и возмущенном (при наличии конуса воды) движение нефти, И.А. Чарный установил точное соотношение, в пределах которого находится истинный предельный безводный дебит:

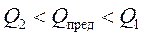. (9.49)

Вычисляя дебиты Q₁ и Q₂ по формулам для известного решения задачи о напорном притоке к несовершенной скважине в пласте постоянной толщины, можно количественно оценить значения Q₁ и Q₂. Расчеты показывают, что верхние и нижние значения предельного дебита (Q₁ и Q₂) различаются в среднем на 25-30%.

Все сказанное выше полностью распространяется на случай прорыва верхнего газа при наличии газовой шапки; при этом под 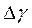следует подразумевать разность объемных весов нефти и газа.

Для практических расчетов используются универсальные графики зависимости безразмерного дебита 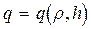и предельной высоты подъема конуса 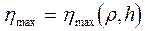, построенные по изложенной методике для кругового однородно-анизотропного пласта с подошвенной водой (рис. 63).

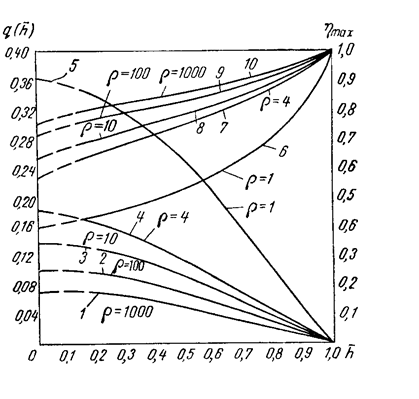
Рис.63

.

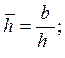
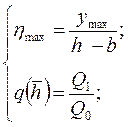
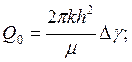
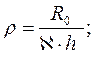
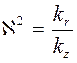Из графиков видно, что при малых 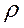, соответствующих большим значением параметра анизотропии пласта 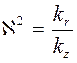, предельный дебит резко возрастает, что подтверждается высокими безводными дебитами нефтяных скважин в пластах с подошвенной водой с малой вертикальной проницаемостью k_z.

Заметим, что величина предельного дебита практически не зависит от конструкции скважины; предельная же депрессия зависит существенно от конструкции скважины и характера вскрытия пласта.

Приведенные выше графики практически также можно использовать для расчетов в пластовых условиях предельных безводных дебитов несовершенных газовых скважин с подошвенной водой.