ОБМОТКА С ДРОБНЫМ ЧИСЛОМ ПАЗОВ НА ПОЛЮС И ФАЗУ

Анализ выражения (3.15), определяющего коэффициент распре­деления, показывает, что амплитуда высших гармонических в кри­вой ЭДС обмотки зависит от угла между векторами ЭДС отдельных катушек. В обмотке с целым q этот угол всегда равен пазовому углу az = 2p π / Z = π/(mq),поэтому для уменьшения k_p высших гармоник необходимо увеличивать число q. Но с увеличением q растет число пазов и соответственно уменьшаются зубцовые деления, ширина зубцов и пазов. Это ограничивает наибольшие допустимые значе­ния q, так как в узких пазах ухудшается заполнение паза медью и ис­того, ширина зубцов не может быть взята меньше предельной, опре­деляемой их допустимой механической прочностью.

Как видно из табл. 3.16, заметное уменьшение k_p большинства высших гармоник происходит уже при q = 3, однако при этом, как показано в § 3.6, k_p для гармоник зубцовых порядков остается таким же, как и для основной гармоники. Чтобы повысить порядок зубцо­вых гармоник и тем самым уменьшить их амплитуду и влияние на характеристики машины, стремятся увеличить число пазов на по­люс и фазу до 4—5 и более. Это легко достижимо в машинах с 2р = 2или 4. Для машин с 2р = 6 или 8 при сравнительно небольших диаметрах статора выполнение q = 4—5 затруднено, а в машинах с большим числом полюсов, особенно в тихоходных с 2р=30—40 и более , вообще невозможно, так как даже при q = 4 в таких машинах необходимо выполнить более 300—400 пазов.

В этих случаях для улучшения кривой поля в воздушном зазоре применяют обмотку, в которой число катушек в катушечных груп­пах не одинаково, а периодически меняется. При этом относитель­ное положение векторов ЭДС катушек различных катушечных групп фазы изменяется по сравнению с обмоткой, в которой число катушек во всех группах постоянно, и угол между векторами ЭДС катушек после соединения схемы становится меньше a_z. Среднее число q при этом получается дробным, и обмотки называют «об­мотками с дробным q». Для того чтобы оценить преимущества при­менения обмоток с дробным, проведем сравнение процессов формирования поля в машинах с целыми и дробными числами пазов на полюс и фазу.

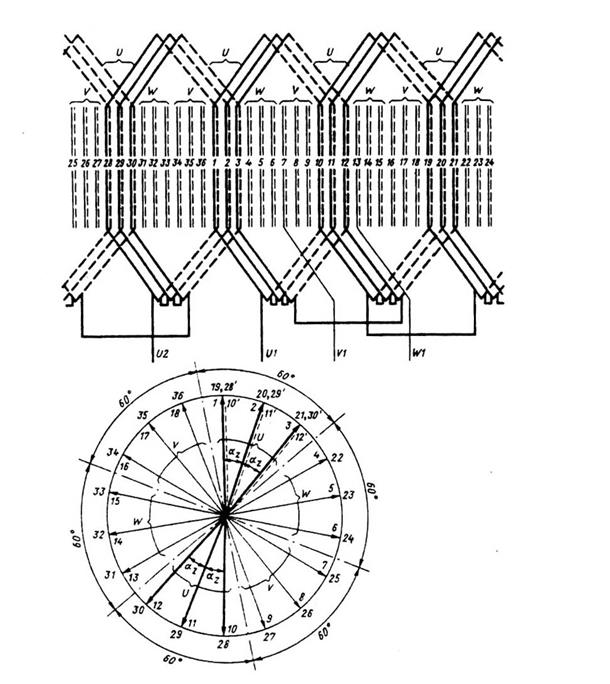
Рис. 3.29. Схема и векторная диаграмма ЭДС катушек фазы обмотки с целым числом пазов на полюс и фазу, Z = 36, 2p = 4, a = 1, q = 3

На рис. 3.29 приведены схема-развертка первой фазы четырехполюсной обмотки с q =3 и векторная диаграмма ЭДС катушек этой фазы. На окружности цифрами без штрихов обозначены номера па­зов статора. Внутренний ряд цифр соответствует пазам, в которых лежат стороны катушек, образующие первую пару полюсов (двойное полюсное деление занимает электрический угол 360°), наружный ряд цифр — пазам второй пары полюсов.

Условимся, что вектор ЭДС первой от начала отсчета катушки направлен от центра диаграммы к отметке на окружности, соответ­ствующей первому пазу, и присвоим этой катушке номер 1. Тогда векторы ЭДС всех последующих катушек обмотки будут направле­ны на отметки, соответствующие следующим номерам пазов соглас­но принятому порядку отсчета — по часовой стрелке.

В рассматриваемой схеме a_z = 180°/ (mq) = 180°/ (3∙3) = 20°. Со­гласно схеме обмотки три первые катушки (q =3) образуют первую катушечную группу фазы U, и векторами их ЭДС будут векторы 1, 2 и 3. Далее по обходу окружности векторной диаграммы следуют векторы ЭДС катушек второй и третьей катушечных групп, принад­лежащих фазе W,— векторы 4, 5,6, и фазе V— векторы 7, 8и 9. Векторы 10, 11и12являются векторами ЭДС катушек четвертой ка­тушечной группы, принадлежащей фазе U, а следующие за ними (13—18)— векторами пятой и шестой катушечных групп (фазы W и V). На этом обход первых двух полюсных делений заканчивается. При обходе следующего двойного полюсного деления картина пол­ностью повторяется.

Первая и четвертая катушечные группы, принадлежащие фазе U, всхемах двухслойных обмоток с 60-градусной фазной зоной всегда включены встречно. Поэтому векторы катушек четвертой катушеч­ной группы (10, 11 и 12)на векторной диаграмме должны быть по­вернуты на 180°. Повернутое положение этих векторов показано на диаграмме пунктиром, а их номера обозначены прежними цифрами, но со штрихами (10', 11', 12').Повернутые векторы полностью сов­падают со сходными векторами ЭДС катушек первой катушечной группы. При обходе следующего двойного полюсного деления та­кое положение сохраняется. В общем случае совпадение векторов ЭДС сходных катушек, включенных встречно, катушечных групп одной фазы сохраняется при любом целом числе q, так как сходные катушки двух соседних групп фазы всегда располагают по окружно­сти зазора на расстоянии 3q пазовых делений, образующих центра­льный угол а = 3q = 180°.

Таким образом, в обмотках с целым q угол между векторами ЭДС катушек фазы после соединения обмотки определяется количе­ством катушек в катушечной группе, которое для всей обмотки по­стоянно и равно q. Следовательно, коэффициент распределения та­ких обмоток зависит только от числа q.

Следует также отметить, что в обмотках с целым q угол между векторами ЭДС катушек может быть определен на векторной диа­грамме по положению векторов ЭДС первой катушечной группы, т. е. процесс формирования обмотки заканчивается после обхода одного полюсного деления по окружности зазора. При дальнейшем обходе векторы ЭДС всех остальных катушек фазы после соедине­ния схемы совпадают со сходными векторами ЭДС катушек первой катушечной группы.

Обмотки с дробным q состоят из катушечных групп с разным числом катушек, поэтому сходные катушки двух соседних групп фазы располагают по окружности зазора на расстоянии, отличном от 3q, т. е. не так, как в обмотках с целым q. Следовательно, центра­льный электрический угол между ними не будет равен 180°, и при встречном включении катушечных групп (при повороте векторов ЭДС катушек на 180° на векторной диаграмме) совпадения векторов ЭДС сходных катушек не произойдет.

Рассмотрим схему одной из простейших обмоток с дробным чис­лом пазов на полюс и фазу [Z = 30, 2р= 4, m = 3, q = Z/ (2pm) = 30/ (4∙3) = 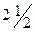], развернутая схема одной фазы которой и векторная диаграмма ЭДС катушек этой фазы приведены на рис. 3.30.

Для расчета и анализа схем обмоток дробное число q обычно выражается неправильной дробью:

q = b + 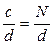(3.19)

где b — целая часть дробного q; с— числитель дробной части q; d — знаменатель дробной части q, называемый часто знаменателем дробности обмоток; N — числитель неправильной дроби, выражающей число q, причем N = bd + с.

Применяя эти обозначения для обмотки с q = 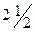, можем записать b = 2;

c = l; d = 2; N = 2 x 2 + l = 5.

Обратим внимание на некоторые закономерности схемы, харак­терные для всех обмоток с дробным q. Катушечные группы не могут состоять из дробного числа катушек, поэтому числа катушек в груп­пах подбирают таким образом, чтобы дробному q соответствовало среднее число катушек в катушечных группах. Для этого катушеч­ные группы в обмотках с дробным q выполняют большими и малы­ми. В больших катушечных группах на одну катушку больше, чем в малых. Большие и малые катушечные группы чередуются между со­бой с определенной периодичностью.

Рассматриваемая обмотка состоит из равного числа больших и малых катушечных групп, содержащих соответственно по три и по две катушки каждая (в среднем по 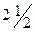катушки в группе). Число ка­тушек в малых катушечных группах всегда равно b, а в больших b + 1 . Чередование больших и малых групп вдоль зазора записыва­ется рядом цифр, определяющих количество катушек в последовательно расположенных катушечных группах. Для рассматриваемого примера таким рядом будет |32|22|32... Из этой записи следует, что первой от начала отсчета будет большая катушечная группа, состо­ящая из трех катушек, затем малая,

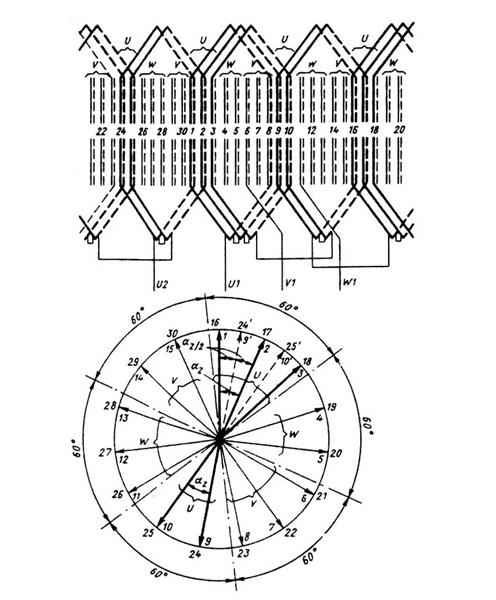
Рис. 3.30. Схема и векторная диаграмма ЭДС катушек фазы обмотки с дробным числом пазов на полюс и фазу, Z = 30, 2p = 4, a = 1, q =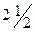

состоящая из двух катушек, затем опять большая и т. д. Чередование имеет строго определенную для каждой обмотки периодичность. В данной обмотке в каждом периоде (периоды разделены вертикальными линиями) имеются по две катушечные группы и по 2 + 3 = 5 катушек. В общем случае в дробных обмотках в каждом периоде чередования содержится по d катушечных групп и по N катушек. При этом условии среднее число катушек в группе за один период будет равно q,так как N/d = q.

На рис. 3.30, так же как и в разобранном ранее примере (см. рис. 3.29), толстыми линиями показаны векторы ЭДС фазы. В первой катушечной группе фазы содержатся три катушки (векто­ры 1, 2, 3).Далее по обходу окружности диаграммы следуют векторы ЭДС катушек второй катушечной группы, принадлежащие фазе W, их два (4и 5). В третьей катушечной группе (фаза V)три катуш­ки. Векторы их ЭДС на диаграмме 6, 7 и 8. Четвертая катушечная группа принадлежит фазе Uи содержит две катушки, векторы их ЭДС 9 и 10. Далее по обходу следуют большая катушечная группа фазы W с тремя катушками (векторы 11, 12. 13)и малая фазы V (век­торы 14 и 15). На этом обход двойного полюсного деления заканчи­вается.

При соединении схемы, как всегда в двухслойных обмотках, сле­дующие друг за другом в фазе катушечные группы включают встречно. Для фазы Vэто первая и четвертая катушечные группы. Повернув на диаграмме векторы ЭДС четвертой катушечной груп­пы на 180° (новые положения векторов показаны пунктиром, а их номера обозначены 9' и 10'), убеждаемся, что в обмотке с дробным q их новое направление не совпадает с направлением векторов ЭДС катушек первой группы, как это было в обмотках с целым q.В дан­ной обмотке при q = 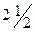они занимают среднее положение, деля угол между векторами ЭДС катушек первой группы пополам. Дей­ствительно, между катушками 1и 9 заключено восемь зубцовых де­лений, соответствующих центральному углу 8a_z = 8 х 24 = 192°, и после поворота вектора 9 на 180° образуется электрический угол 192 - 180 = 12°,равный a_z /2. Таким образом, после соединения схемы векторы ЭДС катушек одной фазы в обмотке с q = 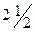располагают­ся со сдвигом между собой на электрический угол a_z /2.

Если в обмотке знаменатель дробности числа q будет больше 2, например, 4 или 5 и т. д., то электрический угол между сходными векторами последовательных катушечных групп фаз после соедине­ния обмотки будет уменьшаться. В общем случае этот угол состав­ляет

dz/ d = π/ (mqd) = π/ (mN).

Поэтому выражение для коэффициента распределения обмоток с дробным q записывается следующим образом:

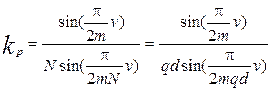, (3.20)

где N = bd + с = qd — числитель неправильной дроби, определяющей число q.

Следовательно, применив обмотку с дробным q, можно полу­чить такое же значение k_р, т. е. такие же результаты, с точки зрения подавления высших гармонических, как и при увеличении числа пазов в машине. Это достоинство обмоток с дробным q привело к их широкому

распространению в крупных тихоходных машинах пере­менного тока.

Следует отметить, что формула (3.20) является общей для расчета коэффициента k_робмоток с целыми и дробными числами q, так как при целых q [см. (3.15)] знаменатель дробности обмоток d = 1 и с = 0.

Выбор знаменателя дробности d, от которого в основном зави­сит угол между ЭДС катушек фазы, определяется условиями сим­метрии обмотки и необходимым числом параллельных ветвей. Об­мотка будет симметричной, если общее число катушечных групп фазы, равное 2р, содержит целое число периодов чередования боль­ших и малых катушечных групп. В каждом периоде содержится d катушечных групп, следовательно, условием симметрии будет крат­ность числа катушечных групп в фазе (2р)числу катушечных групп в периоде (d),т. е. 2p/ d равно целому числу, при этом число катушек в фазе двухслойной обмотки, равное Z/ m, будет кратно числу кату­шек в периоде N, так как

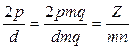
равно целому числу.

Параллельные ветви в обмотке с дробным q могут быть образо­ваны только из катушечных групп, составляющих целое число пери­одов чередования, так как ЭДС отдельных катушечных групп сдви­нуты между собой по фазе, а ЭДС больших и малых катушечных групп не равны по амплитуде. При этом условии допустимое число параллельных ветвей

а = 2p/ (dk), (3.21)

где k – любое целое число.

Максимально возможное число параллельных ветвей

а = 2p/ d. (3.22)

При составлении схем обмоток, в которых числитель дробной части числа q равен с = 1 или с = d – 1,последовательность чере­дования больших и малых катушечных групп безразлична. На­пример, для обмоток с q = 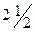может быть принято чередование |2223|2223| или |2232|2232| или любое другое, образованное пере­становкой этих же цифр. Эти чередования отличаются друг от друга только выбором начальной катушки первой фазы и полно­стью равноценны.

В других случаях, когда 1 < с < (d - 1), например, в обмотках с q = 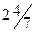или q = 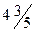и т. д., наиболее благоприятное с точки зрения симметрии обмотки чередование катушечных групп находят раз­личными способами. Наиболее удобный из них заключается в следующем.

По значениям q = b + (c/ d}составляют таблицу, имеющую с строк и d столбцов (рис. 3.31). В клетки таблицы вписывают числа катушек в катушечных группах. За­полнение таблицы начинают с верхней новой клетки в последовательности, показанной на рис. 3.31 стрелками. Сначала в клетки вписывают числа катушек, содер­жащихся в больших катушечных группах. Этими цифрами заполняют столько клеток, сколько в периоде держится больших катушечных групп, т. е. с клеток — весь первый столбец.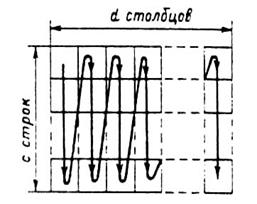

Рис. 3.31. К составлению таблиц чередования катушечных групп в обмотке с дробным q

Продолжая заполнение табли­цы в указанном порядке, вписывают в следующие клетки числа катушек, содержащихся в малых катушечных группах, столько раз, сколько их есть в периоде чередования, т. е. d - с. Далее опять впи­сывают числа катушек в больших катушечных группах, потом в малых и т. д. Вписывание продолжают в той же последовательности, пока все клетки таблицы не будут заполнены. Нужное чередование катушечных групп в периоде читают по строкам заполненной таб­лицы.

Для пояснения этого метода приведем пример определения воз­можных чередований больших и малых групп для обмотки с q = 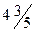. В этой обмотке b = 4, с = 3, d = 5.

Составим таблицу, имеющую с=3 строки и d = 5столбцов. Каждый период чередования катушечных групп обмотки будет содержать с = 3 большие катушечные группы, состоящие из b + 1 = 4 + 1 = 5 катушек, и d – c = 5 – 3 = 2 малые группы, состоящие из b = 4 катушек каждая. Впи­сываем в клетки первого столбца, начиная с верхней, три (по числу больших катушечных групп) цифры 5 — число катушек в больших катушечных группах, заполняя весь первый столбец. Далее, начиная с верхней клетки второго столбца, вписываем в две клетки (по числу малых катушечных групп в периоде) цифры 4 — число катушек в малых группах. Далее продолжаем запись, заполняя клетки таблицы в указан­ной последовательности:

По строкам таблицы читаем нужное чередование больших и малых катушечных групп. Все три строки таблицы показывают одно и то же чередование, изменяется только начало отсчета первой катушечной группы, следовательно, для построения обмотки можно взять любое из трех,

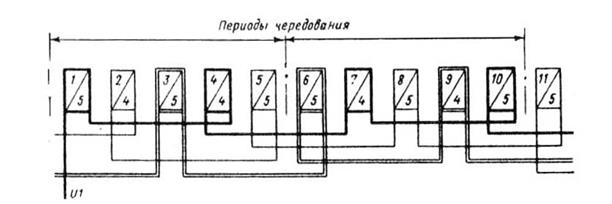
Рис.3.32. Элемент условной схемы обмотки с q =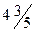

например первую строку |54545|54545|... или вторую строку |54554|54554|...

Условные схемы обмоток с дробным q такие же, как и для обмоток с целым q. Меняя только числа, обозначающие количество катушек в катушечных группах, проставляемые под диагоналями в прямоугольниках. На рис. 3.32 приведена часть условной схемы об­мотки с q = 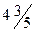. Цифры под диагоналями прямоугольников повто­ряют найденное в описанном примере чередование больших и ма­лых катушечных групп.

В практике построения трехфазных обмоток с дробным q избега­ют применять знаменатель дробности, равный или кратный трем, так как в этом случае симметрия обмотки трехфазных машин нару­шается. При необходимости применить обмотку со знаменателем дробности d,равным или кратным трем, следует провести более глу­бокий анализ возможных вариантов [13].

Начала фаз в обмотках с дробным q, так же как и в обмотках с целым q,должны быть выбраны через 120°∙k,т. е. через 120°∙k/az = 2qkпазовых делений, где k — целое, не кратное трем, число. Од­нако при дробном q произведение 2qkне при всяком kбудет равно целому числу пазовых делений (за исключением обмотки, в которой d = 2). Поэтому в обмотках с дробным q при определении положе­ния начал фаз множитель kнеобходимо выбирать таким, чтобы произведение 2qk было равно целому числу, при этом kне должно быть кратным трем. Наименьшее возможное расстояние между на­чалами фаз, выраженное в пазовых делениях, будет:

при d четном (k = d/ 2)

2qk = 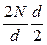= N;(3.23)

при d нечетном (k = d)

2qk = 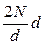= 2N; (3.24)

Большую работу по расчету и внедрению в серию RA обмоток дробным q провел на ЯЭМЗ В.И. Попов [13]. Там же приведен целый ряд новых схем обмоток с дробным q.