Силовой анализ зубчатых механизмов на примере цилиндрических передач
Нормальное функционирование (работоспособность) передач, прежде всего, определяется нагрузкой на механизм, характеризуемой силовыми параметрами, которые нагружают ее при эксплуатации. Нагрузка на элементы машин и механизмов, в том числе и зубчатые передачи, как отмечалось ранее, прежде всего формируется статическим и динамическим сопротивлением движению рабочего органа при его функционировании, приведенным к анализируемым элементам. Первичный силовой анализ проводится при установившемся движении ( 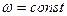 ). Задача силового анализа механических передач, в том числе зацеплением, заключается в определении действующих в контактирующих элементах сил. Исходными данными для выполнения задачи являются крутящие моменты на шестерне
). Задача силового анализа механических передач, в том числе зацеплением, заключается в определении действующих в контактирующих элементах сил. Исходными данными для выполнения задачи являются крутящие моменты на шестерне 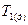 и колесе
и колесе 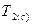 , либо на одном из них, вид передачи и ее геометрические параметры ( диаметры делительных окружностей
, либо на одном из них, вид передачи и ее геометрические параметры ( диаметры делительных окружностей 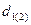 ; угол зацепления
; угол зацепления 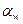 ; угол наклона зубьев
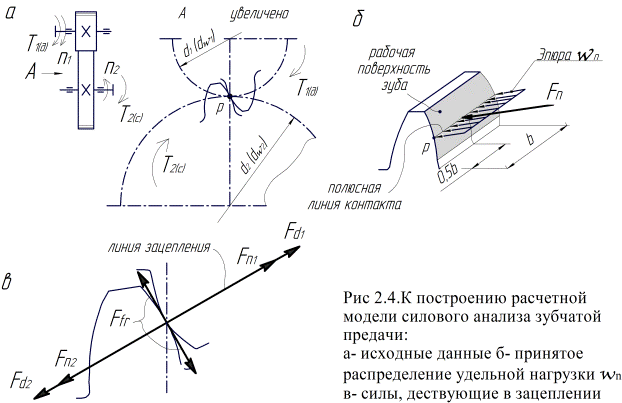
; угол наклона зубьев 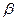 и т.д.). Значения Т1 и Т2 заданы в техническом задании на проектирование передачи в целом, а геометрические параметры устанавливаются в проектных расчетах на предыдущих этапах процесса проектирования, а в проверочных – также заданы в ТЗ (рис.2.4а).
и т.д.). Значения Т1 и Т2 заданы в техническом задании на проектирование передачи в целом, а геометрические параметры устанавливаются в проектных расчетах на предыдущих этапах процесса проектирования, а в проверочных – также заданы в ТЗ (рис.2.4а).
Основные положения модели расчетной:
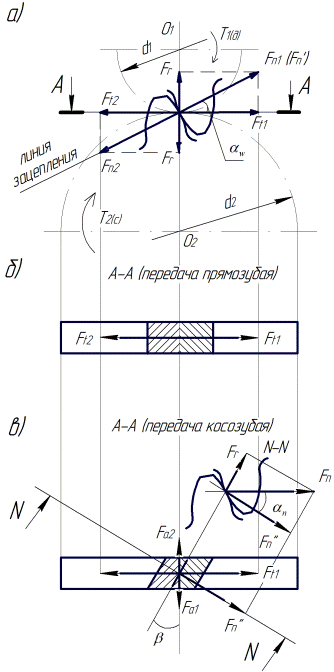
1. Силы взаимодействия зубьев как векторные величины характеризуются точками приложения, направлением и модулем. При выборе точки приложения этих сил руководствуются следующим. Из теории работы зубчатых механизмов известно, что при вращении колес линия контакта зубьев перемещается от головки зуба до ее ножки, образуя рабочую (активную) поверхность (рис.4.2б), и сила взаимодействия по высоте зуба в силу изменения радиуса ее приложения будет переменной. В силовых расчетах зубчатых передач обычно пренебрегают изменением плеча этой силы и считают точкой приложения полюс зацепления.
2. Построение модели силового анализа любого технического устройства, в том числе обсуждаемого, начинают с выявления физической природы сил, возникающих в нем при эксплуатации.
2.1. Передача движения с ведущего элемента на ведомый в передачах зацеплением осуществляется давлением зубьев шестерни и колеса 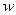 , по соответствующим линиям контакта. В силовых моделях полагают удельное нормальное давление
, по соответствующим линиям контакта. В силовых моделях полагают удельное нормальное давление 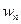 равномерно распределенным по длине линии контакта (ширине зуба – b) передач зацеплением и поэтому его заменяют равнодействующей
равномерно распределенным по длине линии контакта (ширине зуба – b) передач зацеплением и поэтому его заменяют равнодействующей 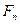 , приложенной в среднем по ширине зуба сечении (рис.2.4б). Для контактирующих неподвижных тел, как известно, эта сила направлена по нормали к поверхностям контакта.
, приложенной в среднем по ширине зуба сечении (рис.2.4б). Для контактирующих неподвижных тел, как известно, эта сила направлена по нормали к поверхностям контакта.
2.2. В связи с наличием относительного движения (перекатывания) зубьев, в зацеплении будет иметь место сила трения, величина которой 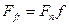 (рис.2.4б). При коэффициенте трения качения
(рис.2.4б). При коэффициенте трения качения 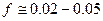 данной силой по ее малости пренебрегают. В этом случае суммарную силу взаимодействия зубьев, как и силу давления, можно направить по нормали и принять равной
данной силой по ее малости пренебрегают. В этом случае суммарную силу взаимодействия зубьев, как и силу давления, можно направить по нормали и принять равной 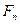 .
.
2.3. В силу неизбежных при изготовлении зубчатых колес ошибок в шаге при постоянной мгновенной угловой скорости ведущего зубчатого колеса 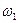 , скорость
, скорость 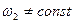 , даже при установившемся движении, что приводит к возникновению в зацеплении динамического момента
, даже при установившемся движении, что приводит к возникновению в зацеплении динамического момента 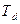 и соответствующей силы
и соответствующей силы 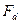 (рис.2.4в):
(рис.2.4в):
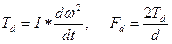 ,
,
где 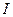 - приведенный момент инерции. В общепринятой методике первичного силового анализа динамическую силу опускают, а учитывают ее непосредственно в прочностных расчетах зубчатых передач (см. ниже).
- приведенный момент инерции. В общепринятой методике первичного силового анализа динамическую силу опускают, а учитывают ее непосредственно в прочностных расчетах зубчатых передач (см. ниже).
Расчетная схема для определения модуля силы взаимодействия и ее составляющих строится на основе предыдущих положений модели силового анализа (рис. 2.4). При этом силу взаимодействия 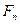 для удобства дальнейших расчетов принято раскладывать на составляющие: тангенциальную –
для удобства дальнейших расчетов принято раскладывать на составляющие: тангенциальную – 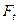 , радиальную –
, радиальную – 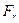 и осевую –
и осевую – 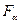 . Определение составляющих силы взаимодействия при заданных крутящих моментах
. Определение составляющих силы взаимодействия при заданных крутящих моментах 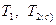 естественно начать с тангенциальных составляющих
естественно начать с тангенциальных составляющих 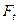 (рис 2.5а).
(рис 2.5а).
Из условий равновесия шестерни и колеса 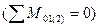 (рис 2.5а) можно записать:
(рис 2.5а) можно записать:
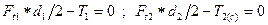
Отсюда, как для прямозубой, так и косозубой передач, при пренебрежении потерями в зацеплении:
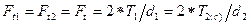 (2.1)
(2.1)
В соответствии с условиями равновесия окружные составляющие направляют так, чтобы они уравновешивали моменты (движущий 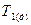 на шестерне и момент сопротивления
на шестерне и момент сопротивления 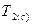 на колесе).
на колесе).
Для радиальных составляющих в цилиндрических передачах, как и для тангенциальных, очевидно соотношение 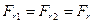 . Величина этой составляющей в прямозубой передаче (рис 2.5a):
. Величина этой составляющей в прямозубой передаче (рис 2.5a):
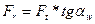 (2.2)
(2.2)
В косозубой передаче радиальную составляющую в соответствии с (рис 2.5в) можно записать в следующем виде:
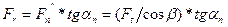 , (2.3)
, (2.3)
где 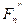 - проекция силы
- проекция силы 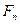 на плоскость А-А. Радиальную составляющую естественно направляют по радиусу к центру зубчатого колеса.
на плоскость А-А. Радиальную составляющую естественно направляют по радиусу к центру зубчатого колеса.
Осевые составляющие в прямозубой передаче в соответствии с (рис.2.5б) равны нулю, а в косозубой по (рис 2.5в)
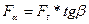 ; (2.4)
; (2.4)
Осевые составляющие 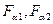 направлены к рабочим поверхностям соответствующих зубьев, как и силы
направлены к рабочим поверхностям соответствующих зубьев, как и силы 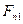 ,
, 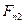 (рис 2.5 в).
(рис 2.5 в).
Сила взаимодействия для прямозубой передачи (рис 2.5а):
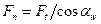 ; (2.5)
; (2.5)
а для косозубой (рис 2.5в):
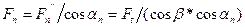 (2.6)
(2.6)

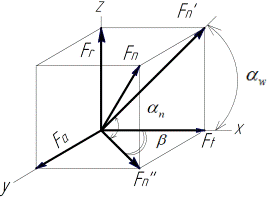
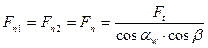
- сила давления зубьев;
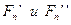 - проекции силы давления соответственно на плоскости ZX и YX в косозубой передаче;
- проекции силы давления соответственно на плоскости ZX и YX в косозубой передаче;

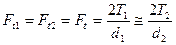 - окружные (тангенциальные) составляющие;
- окружные (тангенциальные) составляющие;
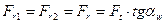 -
-
радиальные составляющие;
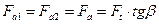 -
-
осевые составляющие в косозубой передаче
Дата добавления: 2016-10-26; просмотров: 2379;











