Функциональные зависимости и их свойства
Для объединения множеств атрибутов употребляются следующие обозначения:
если наименование атрибута имеет смысл, то вместо знака объединения ставится один пробел;
если атрибут обозначается произвольной латинской буквой, то знак объединения не ставится; запись XY эквивалентна X 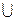 Y.
Y.
Множество атрибутов Y функционально зависит от множества атрибутов X, где X, Y 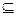 {A1,А2,...,An}, если значения атрибутов в X единственным образом определяют значения атрибутов Y. В этом случае говорят, что между множествами атрибутов X и Y существует функциональная зависимость (F-зависимость), или X определяет Y; обозначают F : X
{A1,А2,...,An}, если значения атрибутов в X единственным образом определяют значения атрибутов Y. В этом случае говорят, что между множествами атрибутов X и Y существует функциональная зависимость (F-зависимость), или X определяет Y; обозначают F : X  Y или просто X
Y или просто X  Y.
Y.
Пример 3.1. Рассмотрим отношение ПОСТАВКИ (ПОСТАВЩИК, ГОРОД, ТОВАР, КОЛИЧЕСТВО). На значения атрибутов этого отношения накладываются следующие ограничения:
1) Осуществлять поставку данного товара в данном количестве из определенного города может только один поставщик;
2) Некоторый поставщик из данного города и в данном количестве может осуществлять поставку только одного товара;
Перечисленные ограничения являются F-зависимостями и их можно записать так:
1) ТОВАР ГОРОД КОЛИЧЕСТВО  ПОСТАВЩИК
ПОСТАВЩИК
2) ГОРОД ПОСТАВЩИК КОЛИЧЕСТВО  ТОВАР
ТОВАР
Пусть R(A1,А2,...,An) — схема отношения, X и Y — подмножества атрибутов. Будем говорить, что отношение R удовлетворяет F-зависимости X  Y, если для любых кортежей t1,t2
Y, если для любых кортежей t1,t2  R из t1(X)=t2(X) следует t1(Y)= t2(Y). В F-зависимости X
R из t1(X)=t2(X) следует t1(Y)= t2(Y). В F-зависимости X  Y подмножество X называется левой, а Y — правой частью.
Y подмножество X называется левой, а Y — правой частью.
Такая интерпретация F-зависимости является основой алгоритма ЗАВИСИМОСТЬ.
Вход. Отношение R и F-зависимость X  Y.
Y.
Выход. Истина, если R удовлетворяет X  Y, в противном случае — ложь.
Y, в противном случае — ложь.
Шаг 1. Сортировать отношение R по Х-столбцам так, чтобы собрать кортежи с равными X-значениями.
Шаг 2. Если каждая совокупность кортежей с равными X-значениями имеет также равные Y-значения, то на выходе получаем истину, в противном случае — ложь.
F-зависимостыо X  Y на множестве атрибутов А можно считать упорядоченную пару (X,Y), где X,Y
Y на множестве атрибутов А можно считать упорядоченную пару (X,Y), где X,Y 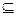 A. Тогда множеством всех функциональных зависимостей над А будет L={(X, Y)| X
A. Тогда множеством всех функциональных зависимостей над А будет L={(X, Y)| X 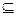 A, Y
A, Y 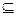 A}.
A}.
Если Y не зависит от X, то записывают X 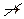 Y. Если X
Y. Если X  Y и Y
Y и Y  X, то X и Y называют эквивалентными или говорят, что между X и Y существует биекция, т. е. X
X, то X и Y называют эквивалентными или говорят, что между X и Y существует биекция, т. е. X 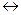 Y.
Y.
Пример 3.2. Пусть поставщик осуществляет поставки ТОВАРА, определенное КОЛИЧЕСТВО. Он находится в ГОРОДЕ и определенной СТРАНЕ. Можно сформировать следующие зависимости:
f1: ТОВАР  КОЛИЧЕСТВО,
КОЛИЧЕСТВО,
f2: ТОВАР  ПОСТАВЩИК,
ПОСТАВЩИК,
f3: ПОСТАВЩИК  ГОРОД,
ГОРОД,
f4: ГОРОД  СТРАНА,
СТРАНА,
f5: ТОВАР  СТРАНА.
СТРАНА.
Аксиомы вывода
Для различных состояний отношения R(A) могут существовать разные совокупности F-зависимостей. Интерес представляет выявление множества F-зависимостей F, которым удовлетворяют все допустимые состояния R(A). Для этого нужно знать семантические связи между атрибутами отношения. Такое множество F-зависимостей можно считать заданным в схеме отношения R(A). В подобном случае любое отношение со схемой R(A) должно удовлетворять всем F-зависимостям из F. Данное множество F конечно, так как существует только конечное число подмножеств множества А. Одним из способов его нахождения является использование алгоритма ЗАВИСИМОСТЬ, что требует много времени. Другим способом являются аксиомы вывода — правила, позволяющие на основании данного множества F-зависимостей получить все F-зависимости, которым удовлетворяет отношение R(A). Рассмотрим эти аксиомы.
Пусть X, Y, Z, W — непустые подмножества множества A={A1,А2,...,An}. Тогда для любого отношения со схемой R(A) справедливы следующие аксиомы вывода.
F1. Рефлексивность: Х  Х.
Х.
F2. Транзитивность: если X  Y и Y
Y и Y  Z, то X
Z, то X  Z.
Z.
F3. Пополнение: если X  Y, то XZ
Y, то XZ  Y.
Y.
F4. Псевдотранзитивность: если X  Y и YZ
Y и YZ  W, то XZ
W, то XZ  W.
W.
F5. Аддитивность: если X  Y и X
Y и X  Z, то X
Z, то X  YZ.
YZ.
F6. Проективность: если X  FZ, то X
FZ, то X  Y или Х
Y или Х  Z.
Z.
Рассмотрим сформулированные аксиомы на примере отношения R, включающего атрибуты: X — ТОВАР, У — ПОСТАВЩИК, Z — ГОРОД, W — СТРАНА.
F1. Рефлексивность. Отношение πX( 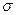 X=x(R)) всегда имеет не более одного кортежа. Следовательно, Х
X=x(R)) всегда имеет не более одного кортежа. Следовательно, Х  Х всегда истинно в R. Например, ТОВАР
Х всегда истинно в R. Например, ТОВАР  ТОВАР.
ТОВАР.
F2. Транзитивность. Пусть t1 и t2 — кортежи в R. Если t1(X) = t2(X), то t1(Y) = t2(Y), а из t1(Y) = t2(Y) вытекает t1(Z) = t2(Z). Таким образом, если
t1(X) = t2(X), то t1(Z) = t2(Z), т. е. R удовлетворяет X  Z. Например, если ТОВАР
Z. Например, если ТОВАР  ПОСТАВЩИК и ПОСТАВЩИК
ПОСТАВЩИК и ПОСТАВЩИК  ГОРОД, то ТОВАР
ГОРОД, то ТОВАР  ГОРОД.
ГОРОД.
F3. Пополнение. Эта аксиома позволяет расширить левую часть F-зависимости. Если R удовлетворяет X  Y, то πY(
Y, то πY( 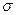 X=x(R)) имеет не более одного кортежа для любого х
X=x(R)) имеет не более одного кортежа для любого х  Х. Если L
Х. Если L 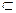 R, то
R, то 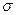 XZ=xz(R)
XZ=xz(R) 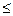
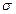 X=x(R) и, следовательно, πY(
X=x(R) и, следовательно, πY( 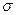 XZ=xz(R))
XZ=xz(R)) 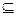 πY(
πY( 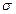 X=x(R)). Таким образом, πY(
X=x(R)). Таким образом, πY( 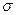 XZ=xz(R)) имеет максимум один кортеж и R должно удовлетворять F-зависимости XZ
XZ=xz(R)) имеет максимум один кортеж и R должно удовлетворять F-зависимости XZ  Y. Например, если ТОВАР
Y. Например, если ТОВАР  ПОСТАВЩИК, то ТОВАР ГОРОД
ПОСТАВЩИК, то ТОВАР ГОРОД  ПОСТАВЩИК.
ПОСТАВЩИК.
F4. Псевдотранзитивность. Пусть t1 и t2 — кортежи в R. По условию если t1(X) = t2(X), то t1(Y) = t2(Y), и аналогично, если t1(YZ) = t2(YZ), то t1(W) = t2(W). Из t1(XZ) = t2(XZ) получаем, что t1(X) = t2(X). Значит, t1(Y) = t2(Y) и, кроме того, t1(YZ) = t2(YZ), откуда следует, что t1(W) = t2(W). Таким образом, R удовлетворяет XZ  W. Например, если ТОВАР
W. Например, если ТОВАР  ПОСТАВЩИК и ПОСТАВЩИК ГОРОД
ПОСТАВЩИК и ПОСТАВЩИК ГОРОД  СТРАНА, то ТОВАР ГОРОД
СТРАНА, то ТОВАР ГОРОД  СТРАНА.
СТРАНА.
F5. Аддитивность. Эта аксиома позволяет объединить две F-зависимости с одинаковыми левыми частями. Из X  Y и X
Y и X  Z следует, что πY(
Z следует, что πY( 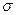 X=x(R)) и πZ(
X=x(R)) и πZ( 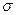 X=x(R)) имеют не более одного кортежа для любого х
X=x(R)) имеют не более одного кортежа для любого х 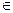 Х. Если бы отношение πYZ(
Х. Если бы отношение πYZ(  X=x(R)) имело более одного кортежа, то по крайней мере одно из отношений πY(
X=x(R)) имело более одного кортежа, то по крайней мере одно из отношений πY(  X=x(R)) или πZ(
X=x(R)) или πZ(  X=x(R)) имело бы более одного кортежа. Таким образом, R удовлетворяет F-зависимости X
X=x(R)) имело бы более одного кортежа. Таким образом, R удовлетворяет F-зависимости X  YZ. Например, если ТОВАР
YZ. Например, если ТОВАР  ПОСТАВЩИК и ТОВАР
ПОСТАВЩИК и ТОВАР  ГОРОД, то ТОВАР
ГОРОД, то ТОВАР  ПОСТАВЩИК ГОРОД.
ПОСТАВЩИК ГОРОД.
F6. Проективность. Эта аксиома в некоторой степени обратна аксиоме аддитивности. Если R удовлетворяет Х  YZ, то πYZ(
YZ, то πYZ(  X=x(R)) имеет не более одного кортежа для любого х
X=x(R)) имеет не более одного кортежа для любого х  Х. Так как πY(πYZ(
Х. Так как πY(πYZ( 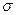 X=x(R))) = πY(
X=x(R))) = πY( 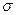 X=x(R)), то πY(
X=x(R)), то πY( 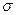 X=x(R)) также может иметь не более одного кортежа. Следовательно, R удовлетворяет Х
X=x(R)) также может иметь не более одного кортежа. Следовательно, R удовлетворяет Х  У. Например, если ТОВАР
У. Например, если ТОВАР  ПОСТАВЩИК ГОРОД, то ТОВАР
ПОСТАВЩИК ГОРОД, то ТОВАР  ПОСТАВЩИК или ТОВАР
ПОСТАВЩИК или ТОВАР  ГОРОД.
ГОРОД.
Некоторые аксиомы вывода могут быть получены из других аксиом. Например, транзитивность F2 является частным случаем псевдотранзитивности F4 при Z = 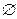 . Аксиома F4 выводится из F1...F3 и F5; если X
. Аксиома F4 выводится из F1...F3 и F5; если X  Y и YZ
Y и YZ  W, то, как следствие, F1, Z
W, то, как следствие, F1, Z  Z. Согласно F3 имеем XZ
Z. Согласно F3 имеем XZ  Y и XZ
Y и XZ  Z. Используя F5, получаем XZ
Z. Используя F5, получаем XZ  YZ. Наконец, применяя F2, имеем XZ
YZ. Наконец, применяя F2, имеем XZ  W.
W.
С помощью аксиом F1, F3 и F4 можно вывести аксиомы F2, F5 и F6. Как было сказано, F2 является частным случаем F4. Если X  Y и X
Y и X  Z, то из F1 получаем YZ
Z, то из F1 получаем YZ  YZ и, дважды применяя F4, сначала получаем XZ
YZ и, дважды применяя F4, сначала получаем XZ  YZ, а затем X
YZ, а затем X  YZ. Поэтому F5 следует из F1, F3 и F4. Для доказательства F6 предположим, что X
YZ. Поэтому F5 следует из F1, F3 и F4. Для доказательства F6 предположим, что X  YZ. Из F1 имеем Y
YZ. Из F1 имеем Y  Y, а из F3 получаем YZ
Y, а из F3 получаем YZ  Y. Применение F4 дает X
Y. Применение F4 дает X  Y.
Y.
Таким образом, аксиомы F1, F3 и F4 составляют полное подмножество для F1...F6 и являются независимыми в том смысле, что ни одна из аксиом не может быть получена из двух других. Аксиомы F1, F3 и F4 иногда называют аксиомами Армстронга.
Система аксиом F1...F6 является полной, т.е. путем одно- или многократного применения к F этих аксиом можно получить любую F-зависимость, которая следует из множества F.
Множество функциональных зависимостей F={f1,f2,...,fm}, находится в приведенной канонической форме, если F-зависимости не имеют одинаковых левых частей. Для таких функциональных зависимостей если Xi  Yi и Xi
Yi и Xi  Yj, то Xi
Yj, то Xi  Yi
Yi 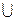 Yj. Например, приведенной канонической формой для F={f1,f2, f3} из примера 3.2 будет:
Yj. Например, приведенной канонической формой для F={f1,f2, f3} из примера 3.2 будет:
ТОВАР  КОЛИЧЕСТВО ПОСТАВЩИК СТРАНА.
КОЛИЧЕСТВО ПОСТАВЩИК СТРАНА.
Замыкания
Пусть F= {Xi  Yi}, 1≤ i ≤n, — множество функциональных зависимостей. Замыканием множества F называют множество F+, содержащее все те зависимости, которые могут быть получены применением к F аксиом Армстронга. Замыкание множества функциональных зависимостей используется для определения биекций и ликвидации избыточности множества функциональных зависимостей.
Yi}, 1≤ i ≤n, — множество функциональных зависимостей. Замыканием множества F называют множество F+, содержащее все те зависимости, которые могут быть получены применением к F аксиом Армстронга. Замыкание множества функциональных зависимостей используется для определения биекций и ликвидации избыточности множества функциональных зависимостей.
Пример 3.3. Пусть F = {АВ  С, С
С, С  В} — множество F-зависимостей на R(A, В, С). Тогда F+ = {А
В} — множество F-зависимостей на R(A, В, С). Тогда F+ = {А  А, AB
А, AB  А, АС
А, АС  A, АВС
A, АВС  А, В
А, В  В, АВ
В, АВ  B, ВС
B, ВС  В, ABC
В, ABC  В, С
В, С  С, АС
С, АС  С, ВС
С, ВС  С, ABC
С, ABC  С, АВ
С, АВ  АВ, ABC
АВ, ABC  АВ, АС
АВ, АС  AC, ABC
AC, ABC  АС, ВС
АС, ВС  ВС, ABC
ВС, ABC  ВС, ABC
ВС, ABC  ABC, АВ
ABC, АВ  С, АВ
С, АВ  АС, АВ
АС, АВ  ВС, AВ
ВС, AВ  ABC, С
ABC, С  В, С
В, С  ВС, АС
ВС, АС  В, АС
В, АС  АВ}.
АВ}.
Вычисление F+ для множества зависимостей F является весьма трудоемкой задачей, так как множество зависимостей F+ может быть большим, даже если само F мало. Рассмотрим множество F = {A  B1, A
B1, A  B2,..., A
B2,..., A  Bn}. Тогда F+ включает все зависимости A
Bn}. Тогда F+ включает все зависимости A  Y, где Y — подмножество множества {B1,B2,...,Bn}. Так как существует 2n таких подмножеств Y, то даже при небольших n их нелегко перечислить.
Y, где Y — подмножество множества {B1,B2,...,Bn}. Так как существует 2n таких подмножеств Y, то даже при небольших n их нелегко перечислить.
Более простым является вычисление замыкания атрибутов множества А относительно множества функциональных зависимостей F. Пусть F — множество функциональных зависимостей на множестве атрибутов U, а X — некоторое подмножество U. Тогда Х+ — замыкание X относительно F — есть множество атрибутов А таких, что зависимость Х  A может быть выведена из F по аксиомам Армстронга. Замыкание X+ позволяет сразу определить, выводится ли зависимость X
A может быть выведена из F по аксиомам Армстронга. Замыкание X+ позволяет сразу определить, выводится ли зависимость X  Y из F по аксиомам Армстронга. Существует следующая лемма.
Y из F по аксиомам Армстронга. Существует следующая лемма.
Утверждение. Функциональная зависимость X  Y выводится из аксиом Армстронга тогда и только тогда, когда Y
Y выводится из аксиом Армстронга тогда и только тогда, когда Y 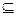 Х+.
Х+.
Рассмотрим алгоритм вычисления замыкания множества атрибутов U относительно множества функциональных зависимостей F.
Вход. Конечные множества: атрибутов U, зависимостей F и атрибутов X 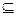 U.
U.
Выход. Замыкание Х+ множества атрибутов X относительно F.
Вычисляем последовательность множеств атрибутов Х(0), Х(1),... по следующим правилам.
Шаг 1. Х(0) есть X.
Шаг 2. Хi+1 есть Xi плюс множество атрибутов А таких, что в F существует некоторая зависимость Y  Z, А принадлежит Z и Y
Z, А принадлежит Z и Y 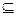 X(i) Поскольку Х = Х(0)
X(i) Поскольку Х = Х(0) 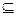 Х(1)
Х(1) 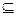 ...
... 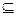 U и U конечно, в итоге достигнем такого i, что X(i) = X(i+1). Отсюда X(i) = X(i+1) =X(i+2) =... и поэтому процесс вычисления Х+ прекращается, если X(i) = X(i+1).
U и U конечно, в итоге достигнем такого i, что X(i) = X(i+1). Отсюда X(i) = X(i+1) =X(i+2) =... и поэтому процесс вычисления Х+ прекращается, если X(i) = X(i+1).
Пример 3.4. Пусть F состоит из следующих зависимостей:
АВ  С, AE
С, AE  G,
G,
ВС  D, D
D, D  EC,
EC,
В  АЕ, EG
АЕ, EG  K,
K,
а Х=АВ. Используя алгоритм, получаем Х(0)=Х=АВ. Для вычисления Х(1) находим зависимости, которые имеют в левой части А, В или АВ. Во множестве F существуют две зависимости: АВ  С и В
С и В  АЕ. Поэтому присоединяем С и E к Х(0) получаем Х(1) =АВСЕ. Затем вычисляем Х(2) путем поиска левых частей зависимостей F, содержащихся в Х(1). Находим BC
АЕ. Поэтому присоединяем С и E к Х(0) получаем Х(1) =АВСЕ. Затем вычисляем Х(2) путем поиска левых частей зависимостей F, содержащихся в Х(1). Находим BC  D и AE
D и AE  G. Таким образом, Х(2)=ABCDEG. Далее находим EG
G. Таким образом, Х(2)=ABCDEG. Далее находим EG  K, D
K, D  G и, наконец, Х(3)=ABCDEGK — множество всех атрибутов. Следовательно, Х(3)= Х(4)= ... . Итак, получаем (AB)+=ABCDEGK.
G и, наконец, Х(3)=ABCDEGK — множество всех атрибутов. Следовательно, Х(3)= Х(4)= ... . Итак, получаем (AB)+=ABCDEGK.
Пусть задано отношение R на множестве атрибутов {A1,А2,...,An}, Множество атрибутов К называется ключом отношения R (первичным ключом), если каждый атрибут Ai 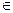 {A1,А2,...,An},, который не входит в К, функционально зависит от К, т. е. К
{A1,А2,...,An},, который не входит в К, функционально зависит от К, т. е. К  Ai; и никакое подмножество К не удовлетворяет этому свойству. В дальнейшем ключевые атрибуты в схемах отношений будут подчеркиваться.
Ai; и никакое подмножество К не удовлетворяет этому свойству. В дальнейшем ключевые атрибуты в схемах отношений будут подчеркиваться.
Пример 3.5. В функциональной зависимости ТОВАР ДАТА КОЛИЧЕСТВО  ГОРОД ПОСТАВЩИК ключом является (ТОВАР ДАТА КОЛИЧЕСТВО).
ГОРОД ПОСТАВЩИК ключом является (ТОВАР ДАТА КОЛИЧЕСТВО).
Два множества F-зависимостей F и G над схемой отношения R эквивалентны, F ≡G, если F+ = G+. Если F ≡G, то F есть покрытие для G.
Пример 3.6. Множества F={A  BC, A
BC, A  D, CD
D, CD  E} и G={А
E} и G={А  ВСЕ, A
ВСЕ, A  ABD, CD
ABD, CD  E} эквивалентны. Множество F не эквивалентно множеству G'={A
E} эквивалентны. Множество F не эквивалентно множеству G'={A  BCDE}, поскольку зависимость CD
BCDE}, поскольку зависимость CD  E не выводится в G'.
E не выводится в G'.
Множество F-зависимостей F неизбыточно, если у него нет такого собственного подмножества F' что F'≡F. Если такое подмножество F' существует, то F избыточно.
Пример 3.7. Множество F={АВ  С, А
С, А  ВС, А
ВС, А  В, В
В, В  С} избыточно, так как есть подмножество F'={A
С} избыточно, так как есть подмножество F'={A  B, B
B, B  C}, которое эквивалентно F.
C}, которое эквивалентно F.
Пусть имеется множество функциональных зависимостей F={Xi  Yi}, i =
Yi}, i = 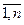 . Множество атрибутов Zi
. Множество атрибутов Zi 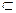 Xi называют посторонним в Xi, если Xi
Xi называют посторонним в Xi, если Xi  Zi
Zi  Yi может быть получено в замыкании F+.
Yi может быть получено в замыкании F+.
Пример 3.8. В примере 3.2 комбинация атрибутов ТОВАР и ПОСТАВЩИК определяет атрибут ГОРОД, т. е. f3 может заменить зависимость
ТОВАР ПОСТАВЩИК  ГОРОД.
ГОРОД.
Из f2 видно, что атрибут ПОСТАВЩИК с левой стороны является посторонним.
Множество F-зависимостей F называют минимальным, если оно содержит не больше F-зависимостей, чем любое эквивалентное множество F-зависимостей.
Минимальное множество F-зависимостей не может содержать избыточных зависимостей. Таким образом, оно одновременно и неизбыточно.
Пример 3.9. Множество G={A  BC, B
BC, B  A, AD
A, AD  E, BD
E, BD  L} неизбыточно, но не минимально, поскольку существует множество F={A
L} неизбыточно, но не минимально, поскольку существует множество F={A  BC, B
BC, B  A, AD
A, AD  EL}, которое эквивалентно G и содержит меньшее число F-зависимостей. Множество F является минимальным покрытием G.
EL}, которое эквивалентно G и содержит меньшее число F-зависимостей. Множество F является минимальным покрытием G.
При проектировании схем БД для минимального покрытия множества F-зависимостей полезно использовать следующие ограничения:
1) правая часть каждой F-зависимости содержит единственный атрибут;
2) ни для какой F-зависимости Х  А в F множество F—(Х
А в F множество F—(Х  А) не эквивалентно F;
А) не эквивалентно F;
3) ни для какой F-зависимости Х  А в F и собственного подмножества Z
А в F и собственного подмножества Z 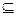 X множества F—(X
X множества F—(X  A)
A) 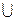 (Z
(Z  A) и F не эквивалентны.
A) и F не эквивалентны.
Пример 3.10. Пусть F состоит из таких F-зависимостей:
AB  C, ACD
C, ACD  B, CG
B, CG  BD,
BD,
C  A, D
A, D  EG, CE
EG, CE  AG,
AG,
BC  D, BE
D, BE  C,
C,
Используя условие 1), получаем
АВ  C, D
C, D  Е, CG
Е, CG  B,
B,
С  A, D
A, D  G, CG
G, CG  D,
D,
ВС  D, BE
D, BE  C, СЕ
C, СЕ  A,
A,
ACD  В, СЕ
В, СЕ  G.
G.
Здесь F-зависимость СЕ  А избыточна, поскольку она следует из зависимости С
А избыточна, поскольку она следует из зависимости С  А. Подобным образом избыточна F-зависимость CG
А. Подобным образом избыточна F-зависимость CG  B, так как из CG
B, так как из CG  D, С
D, С  А и ACD
А и ACD  B получаем CG
B получаем CG  B. Никакие другие F-зависимости не являются избыточными. Однако ACD
B. Никакие другие F-зависимости не являются избыточными. Однако ACD  B может быть замещена зависимостью CD
B может быть замещена зависимостью CD  B, поскольку С
B, поскольку С  А. Таким образом, минимальное покрытие включает следующие F-зависимости:
А. Таким образом, минимальное покрытие включает следующие F-зависимости:
AB  C, CD
C, CD  B, BE
B, BE  C,
C,
C  A, D
A, D  E, CG
E, CG  D,
D,
BC  D, D
D, D  G, CE
G, CE  G.
G.
Другое минимальное покрытие, построенное из F исключением СЕ  А, CG
А, CG  D и АСD
D и АСD  B, имеет вид
B, имеет вид
AB  C, D
C, D  E, CG
E, CG  B,
B,
C  A, D
A, D  G, CE
G, CE  G.
G.
B  CD, BE
CD, BE  C,
C,
Отметим, что эти два минимальных покрытия имеют разное число зависимостей.
Более короткое представление множества F является предпочтительным: во-первых, потому, что от мощности F зависит временная сложность алгоритмов для обработки этого множества; во-вторых, объем используемой памяти и число операций при модификации БД также определяются числом F-зависимостей.
Дата добавления: 2016-10-26; просмотров: 4575;











