Реляционная алгебра
Реляционная алгебра представляет собой совокупность операций высокого уровня над отношениями. Эти операции можно разделить на две группы:
a) пять основных операций - ОБЪЕДИНЕНИЕ, РАЗНОСТЬ, ДЕКАРТОВО ПРОИЗВЕДЕНИЕ, ПРОЕКЦИЯ, ВЫБОР;
b) дополнительные операции не расширяющие возможности основных операций, однако, обеспечивающие краткость записи, - ПЕРЕСЕЧЕНИЕ, СОЕДИНЕНИЕ, СЛИЯНИЕ, ДЕЛЕНИЕ.
Операндами операций реляционной алгебры являются постоянные и (или) переменные отношения. Для операций объединение, разность и пересечение оба участвующих в них отношения должны быть:
Совместимы по объединению (т. е. иметь одинаковую арность и атрибуты, по которым осуществляется операция), определены на одном домене.
Рассмотрим названные операции на примерах отношений R и S:
| R | (A | B | C) | S | (D | E | F) | ||||||
| p | 1 | a | p | 2 | b | ||||||||
| p | 2 | b | p | 3 | a | ||||||||
| p | 2 | c |
Основные операции.Операцией ОБЪЕДИНЕНИЕ отношений R и S называется отношение Т=R 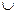 S, включающее множество кортежей, принадлежащих R или S или им обоим. Все кортежи результатного отношения Т имеют одинаковое число компонентов, поскольку операция применяется к отношениям одной и той же арности.
S, включающее множество кортежей, принадлежащих R или S или им обоим. Все кортежи результатного отношения Т имеют одинаковое число компонентов, поскольку операция применяется к отношениям одной и той же арности.
Пример 2.8. Операция ОБЪЕДИНЕНИЕ имеет вид
R 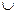 S S
| p | 1 | a |
| p | 2 | b | |
| q | 2 | c | |
| q | 3 | a |
Операцией РАЗНОСТЬ отношений R и S, определенных на общем домене, называется отношение Т=R-S, включающее множество кортежей, принадлежащих R, но не принадлежащих S. Отношения R и S имеют одинаковую арность.
Пример 2.9: Операция РАЗНОСТЬ имеет вид:
| R - S | p | 1 | a |
| q | 2 | c |
Операция ДЕКАРТОВО ПРОИЗВЕДЕНИЕ отношений R и S, которые соответственно имеют арности К1 и К2, называется отношение Т=R×S,включающее множество кортежей длиной К1+К2, первые К1 компонентов которых образуют кортежи, принадлежащие R, а последние К2-кортежи, принадлежащие S. Другими словами, производится конкатенация кортежей из отношений R и S.
Пример 2.10. Операция ДЕКАРТОВО ПРОИЗВЕДЕНИЕ имеет вид
| R х S | (A | B | C | D | E | F) | |||
| p | 1 | a | p | 2 | b | ||||
| p | 1 | a | q | 3 | a | ||||
| p | 2 | b | p | 2 | p | ||||
| p | 2 | b | q | 3 | a | ||||
| q | 2 | c | p | 2 | b | ||||
| q | 2 | c | q | 3 | a |
Пусть t - кортеж отношения R(X) и А – атрибут Х, тогда t[А] - А-компонента кортежа t. Аналогично, если Y - подмножество Х, t[Y] - кортеж (размерности ׀Y׀), который содержит компоненты t, соответствующие элементам Y.
Операцией ПРОЕКЦИЯ R на Y называется отношение R[Y], которое является вертикальным подмножеством столбцов отношения R:
R[Y]={t[Y]|t Є R}
Таким образом, R[Y]-отношение на Y, включающее все кортежи, получаемые из кортежей путем отбора компонентов, соответствующих Y, и удаления одинаковых кортежей (кроме одного) из множества, полученного в результате проектирования.
Другое обозначение для операции проекция πх(R).
Пример 2.11. Операция ПРОЕКЦИЯ имеет вид
R[A C] (A C) S[E F] (E F)
p a 2 b
p b 3 a
q c
Операция ВЫБОР строит горизонтальное подмножество кортежей отношения R, удовлетворяющих определенному предикату. Пусть Θ - одна из бинарных операций «<», «≤», «>», «≥», «=», «≠», применяемая к атрибуту (атрибутам) А и кортежу t. Тогда R[AΘt] - это набор кортежей отношения , каждая А-компонента которых находится в отношении Θ к кортежу t. Вместо кортежа t можно взять множество кортежей В таких, что А и В определяются на общих доменах. Тогда R[AΘB] - это набор кортежей отношения, А-компоненты которых находятся в отношении Θ к В-компонентам.
Пример 2.12. Операция ВЫБОР имеет вид
| R[С≠b] | (A | B | C) | R[A≠q ^ B>1] | (A | B | C) | |
| p | 1 | a | p | 2 | b | |||
| q | 2 | c |
Другим обозначением операции ВЫБОР является σAΘt (R).
Операцией ПЕРЕСЕЧЕНИЕ отношений R и S называется отношение T=R∩S, которое включает кортежи, принадлежащие как R, так и S.Другими словами, R∩S=R-(R-S).
Пример 2.13. Операция ПЕРЕСЕЧЕНИЕ имеет вид
R∩S p 2 b
Пусть R(X, Y) и S(Y, Z) – отношения, где X, Y, Z – непересекающиеся множества атрибутов и Y-множество атрибутов, общее для отношений R и S.
Операцией соединение отношений R и S называется отношение Т (X, Y, Z), определяемое как Т (X, Y, Z)={(х, y, z,)| (х, y) Є S}. Таким образом, отношение Т - это множество кортежей отношений R и S, имеющих одинаковые значения общих атрибутов для этих отношений.
Можно определить операцию СОЕДИНЕНИЕ более широко с точки зрения типа отношения между атрибутами отношений R и S. Пусть даны отношения R(A, B1) S(B2, C), где B1 и B2 определены на общем домене; Θ - одна из бинарных операций «<», «≤», «>», «≥», «=», «≠», в которых могут находиться атрибуты B1 и B2. Операция СОЕДИНЕНИЕ R по B1 и S по B2 (обозначается R[B1ΘB2] S) есть соединение кортежей из отношений R и S, атрибуты которых находятся в отношении Θ.
Пример 2.14. Операция СОЕДИНЕНИЕ имеет вид
| R[A=D] S | (A | B | C | D | E | F) |
| p | a | p | b | |||
| p | b | p | b | |||
| q | c | q | a | |||
R[B≤E 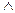 C=F] S C=F] S
| (A | B | C | D | E | F) |
| p | a | q | a | |||
| p | b | p | b | |||
Заметим, что отношения R и S могут иметь одинаковые имена атрибутов, и поэтому имена результатного отношения должны быть определены. Например, для отношений R(A, B) и S(A, B), где А и В определены на общем домене, можно задать следующую операцию СОЕДИНЕНИЕ:
Т(D, E, F, G)=R(A,B) [B>B] S(A, B).
Источником значений для атрибута D в T является атрибут А в R. Аналогично для атрибутов E, F, G и T источниками будут атрибуты B в R, A и S.
Операция СЛИЯНИЕ(естественное соединение) выполняется так же, как СОЕДИНЕНИЕ,при использовании операции «=» между атрибутами или множествами атрибутов отношений; при этом в результатном отношений удаляются одинаковые столбцы. Применим операцию СЛИЯНИЕдля примера 8.
Пример 2.15. Операция СЛИЯНИЕ имеет вид
| R[A*D] S | (A | B | C | E | F) |
| p | a | b | |||
| p | b | b | |||
| q | c | a |
Операция СЛИЯНИЕможет быть также обозначен R 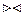 S.
S.
Операция ДЕЛЕНИЕопределяется следующим образом. Пусть даны отношения R(A, B) и P(C), где атрибуты B и C определены на одном домене. Тогда R[B÷C] P – подмножество R[A] (частное), которое получается в результате деления значений атрибута С и S (делитель), т.е. если отношение R и P имеют соответственно арность r и p, где r>p; p≠0. Тогда R÷ P - множество кортежей t длиной r – p таких, что для всех кортежей длиною p, принадлежащих P, кортеж t принадлежит R. Заметим, что декартово произведение R[А] с Р[С] принадлежит отношению R.
Пример 2.16. Пусть задано отношение Р:
Р (В С)
1 a
2 c
Тогда операция ДЕЛЕНИЕимеет вид
R÷Р(А)
р
q
Дата добавления: 2016-10-26; просмотров: 2998;











