Модель данных «сущность-связь»

Модель данных «сущность—связь» ввел в 1976 г. П. П. Чен. Она имеет много общего с иерархической и сетевой моделями данных и в силу своей ориентации на процесс проектирования может рассматриваться как обобщение и развитие ранее рассмотренных моделей. Описываемая модель допускает непосредственное представле­ние связей типа М : N.

Основные понятия. Модель «сущность—связь» базируется на представлении о том, что реальный мир состоит из различных сущностей, связанных определенными отношениями. Категории «сущность» и «связь» объявляются основополагающими, и разделение их производится на этапе создания конкретных представлений некоторой предметной области.

Каждая сущность принадлежит к некоторому классу или ему соответствует некоторый тип. Между сущностями имеются связи, за которыми пользователь закрепляет какой-то класс (тип). Таким образом, класс сущностей и класс связей определяют множества конкретных объектов и связей между ними. Заметим, что некоторая сущность может принадлежать более чем к одному классу (например, поставщик может одновременно быть и потребителем). В каждый момент времени состояние связи S между классами сущностей E₁, Е₂ ..., Е_n определяется отношением между множествами DOM E₁, DOM E₂, ..., DOM Е_n, где DOM Е_i, i= 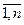— множество объектов типа Е_i.

Множество связей в модели «сущность — связь» можно представить в виде математического отношения п классов объектов:

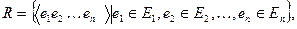
где е_i — сущность, принадлежащая множеству сущностей Е_i, кортеж <e₁ e₂ ... е_п> — связь из множества связей R. Необязательно, чтобы все E_i, на которых определено R, были различными. Совокупность сущностей и классов связей образует верхний уровень модели.

Сущности и связи описываются характерными для них атрибутами. Среди атрибутов какой-нибудь сущности или связи выделяется подсписок, значения атрибутов которой однозначно идентифицируют сущность или связь в пределах типа. Сущности, связи и атрибуты образуют нижний уровень модели.

Графически модель «cущность — связь» представляется в виде схемы, в которой каждому классу объектов соответствует прямоугольник, а классу связей — шестиугольник (рис. 2.7). Под прямоугольником и шестиугольником указываются имена атрибутов сущностей и связей.

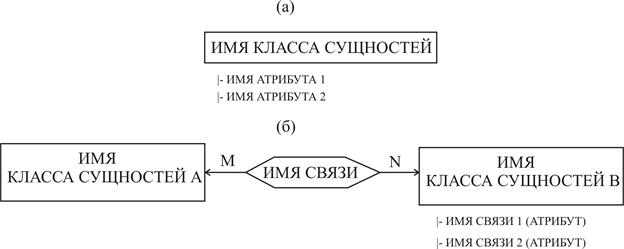
Рис. 2.7. Графическое представление модели «сущность-связь»:

а) класс сущностей; б) класс связей;

При изображении класса сущностей будем придерживаться следующих обозначений: ключевые атрибуты подчеркиваются, два различных класса сущностей не могут иметь одного имени.

На связи накладываются следующие ограничения:

типы связей между классами задаются парами (1:1, 1 : N, N : 1, М : N). Когда значения М и N уточнены, берется максимальное значение;

одна связь может относиться ко многим сущностям и одна сущность может иметь много связей. В случае связей типа 1:1, 1 : N, N : 1 не всегда нужно указывать имя связи.

Рассмотрим пример представления концептуальной схемы БД с помощью модели «сущность—связь» (рис. 2.8). Пусть имеются следующие приложения: управление поставками, складом, производством и договорами. Эти приложения могут использовать такие классы сущностей: ПОСТАВЩИК (поставщики), БАЗ-ДЕТ (базовые детали), ИЗД-УЗЕЛ (изделия и узлы), ДОГОВОР (договоры), СЛУЖАЩИЙ (служащие), ОТДЕЛ (отделы).

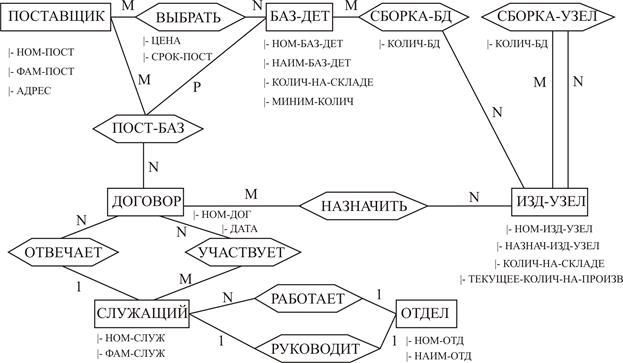Рис. 2.8. Пример схемы модели «сущность—связь»

Для удовлетворения требований указанных выше приложений используются следующие связи между сущностями:

ВЫБРАТЬ — позволяет выбрать поставщика базового продукта в зависимости от условий продажи и поставки (эти условия задаются на схеме);

СБОРКА-БД — указывает базовые детали (материалы), которые непосредственно используются для производства изделия или узла, а также их число;

СБОРКА-УЗЕЛ — указывает узлы, непосредственно входящие в другие узлы или изделия, а также их число;

ПОСТ-БАЗ — связывает в договоре поставщиков с базовыми деталями;

НАЗНАЧИТЬ — характеризует в договоре изделия и узлы;

ОТВЕЧАЕТ — указывает ответственного за договор;

УЧАСТВУЕТ — связывает договор и людей, которые участвуют в его реализации;

РАБОТАЕТ — связывает отдел и людей, которые в нем работают;

РУКОВОДИТ — указывает руководителя данного отдела.

Схема модели «сущность—связь» может быть описана в виде, представленном на рис. 2.8.

Классы сущностей:

E1/ПОСТАВЩИК [НОМ-ПОСТ, ФАМ-ПОСТ, АДРЕС];

Е2/БАЗ-ДЕТ [НОМ-БДЗ-ДЕТ, НАИМ-БАЗ-ДЕТ, КОЛИЧ-НА-СКЛАДЕ, МИНИМ-КОЛИЧ];

Е3/ДОГОВОР [НОМ-ДОГ, ДАТА];

Классы связей:

[ПОСТАВЩИК, БАЗ-ДЕТ, ДОГОВОР];

[ПОСТАВЩИК, БАЗ-ДЕТ : ЦЕНА, СРОК-ПОСТ];

[БАЗ-ДЕТ, ИЗД-УЗЕЛ : КОЛИЧ-БД];

Имена атрибутов связей отделяются двоеточием от имен классов сущностей.

Модель «сущность—связь» включает различные характеристики предметной области.

1. Связь может относиться к нескольким классам сущностей, например, связь ПОСТ-БАЗ соединяет классы сущностей ПОСТАВЩИК, БАЗ-ДЕТ, ДОГОВОР.

2. Связь может многократно относиться к одному классу сущностей, например связь СБОРКА-УЗЕЛ.

3. Многие связи могут относиться к одному классу сущностей, например связи РАБОТАЕТ и РУКОВОДИТ между сущностями СЛУЖАЩИЙ и ОТДЕЛ.

4. Модель отображает различные связи типа 1:1, 1 : N, М : N.

5. Наличие двух классов сущностей для деталей БАЗ-ДЕТ и ИЗД-УЗЕЛ позволяет управлять: поставками деталей и находить поставщиков, опираясь на класс БАЗ-ДЕТ; процессом производства изделий, используя класс ИЗД-УЗЕЛ.

6. Два класса сущностей БАЗ-ДЕТ и ИЗД-УЗЕЛ имеют общие и специфические для них атрибуты. Наличие общих атрибутов приводит к некоторой избыточности данных. Специфические атрибуты требуются областью применения объектов.

В схеме (рис. 2.8) можно было бы рассматривать только функцию продажи изделий. В этом случае внешняя схема включала бы только сущности: базовые детали, узлы, изделия, которые нужно выделить вместе со связями между ними из концептуальной схемы. Во внешней схеме следует различать изделия и узлы, так как некоторая информация, требуемая для продажи, имеет отношение только к изделиям.

Для решения задач управления складом и производством изделий необходимо описать номенклатуру изделий и узлов, указывая: состав изделий из узлов и базовых деталей, состав узлов из подузлов и базовых деталей.

Для указания более конкретных связей между сущностями различают прямую и обратную связи. Каждой такой связи соответствует имя и пара чисел.

Рис. 2.9. Схема прямой и обратной связей

Например, в связи между сущностями СЛУЖАЩИЙ и ОТДЕЛ (рис. 2.9) прямая связь РАБОТАЕТ [1:1] указывает на то, что служащий работает только в одном отделе; обратная связь СОДЕРЖИТ [1 : N] указывает на то, что отдел содержит не менее одного служащего (обычно много служащих). Другими словами, связь L[M, N] между двумя классами сущностей А и В указывает на то, что сущность А связана, как минимум, с M и, как максимум, с N сущностями В. Иногда N может быть не определено.

Модель «сущность—связь» появилась в связи с потребностями проектирования БД. Она удовлетворяет двум важным критериям: во-первых, мощность ее средств позволяет представлять структуры и ограничения, свойственные реальному миру, и, во-вторых, разрыв между возможностями модели и промышленными СУБД не является слишком большим. Эти модели помогают проектировщикам контактировать с пользователями в процессе анализа и конструирования БД.

Реляционная модель

Основные понятия

В реляционной модели данных информация хранится в одной или нескольких связанных таблицах. Отдельная таблица обычно представляет совокупность (группу) либо реальных объектов, либо некоторых абстрактных концепций, либо событий одного типа. Каждая запись в таблице идентифицирует один объект группы. Таблица состоит из строк и столбцов, называемых записями и полями соответственно. Таблицы обладают следующими свойствами:

1. Каждый элемент таблицы представляет собой один элемент данных, т.е. группа значений в одном столбце одной строки недопустима;

2. Все столбцы в таблице однородные. Это означает, что элементы столбца имеют одинаковую природу. Столбцам присвоены имена;

3. В таблице нет двух одинаковых строк;

4. Порядок размещения строк и столбцов в таблице может быть произвольным. В операциях с такой таблицей ее строки и столбцы могут просматриваться в любом порядке безотносительно к их информационному содержанию и смыслу.

Таблицы, обладающие такими свойствами, являются точным прообразом математического двумерного множества – отношения (relation). Но эти два понятия не эквивалентны. Отношение – это абстрактный математический объект, а таблица – это конкретное изображение этого абстрактного объекта. Различие проявляется в их свойствах. В отношении строки и столбцы могут быть неупорядочены, а в таблице строки упорядочены сверху вниз, а столбцы слева направо. Строки в таблице могут повторяться строки, а в отношении нет.

В реляционной модели каждая строка таблицы уникальна. Это обеспечивается применением ключей, которые содержат одно или несколько полей таблицы. Ключи хранятся в упорядоченном виде, обеспечивающем прямой доступ к записям таблицы во время поиска. Связь между таблицами осуществляется посредством значений одного или нескольких совпадающих полей (преимущественно ключевых).

Приведем ряд терминов, применяющихся в реляционной модели:

· Отношением (relation) называется двумерное множество – таблица, удовлетворяющая вышеперечисленным требованиям;

· Атрибут – это свойство, характеризующие объект. В структуре таблицы каждый атрибут имеет имя и ему соответствует заголовок некоторого столбца таблицы. Количество атрибутов называется степенью отношения;

· Кортежом (tuple) называется строка таблицы. В общем случае кортежи представляют собой набор пар <атрибут>, <значение>. Каждое значение должно быть атомарным, т.е. не может быть многозначным или составным. Следовательно, многозначные и составные атрибуты в реляционной модели не поддерживаются. Количество кортежей называется кардинальным числом;

· Домен представляет собой множество всех возможных значений определенного атрибута отношения.

· Первичным ключом называется атрибут отношения, однозначно идентифицирующий каждый из его кортежей. Ключ может быть составным (сложным), т. е. состоять из нескольких атрибутов.

· Потенциальный ключ – это подмножество атрибутов отношения, обладающего следующими свойствами:

- Свойством уникальности. Нет одинаковых кортежей с теми же значениями потенциальных ключей;

- Свойством неизбыточности. Никакое из подмножеств потенциального ключа не обладает свойством уникальности.

Каждое отношение обязательно имеет комбинацию атрибутов, которая может служить ключом. Его существование гарантируется тем, что отношение – это математическое множество, которое не может содержать одинаковых кортежей, т.е. по крайней мере вся совокупность атрибутов обладает свойством однозначной идентификации кортежей отношения. Возможны случаи, когда отношение имеет несколько комбинаций атрибутов, каждая из которых однозначно определяет все кортежи отношения. Все эти комбинации атрибутов являются потенциальными или возможными ключами отношения. Один потенциальный ключ выбирается в качестве первичного, остальные будут называться вторичными (альтернативными). Могут быть даже такие ситуации, когда любой из потенциальных ключей может быть выбран в качестве первичного. Примером может служить таблица Менделеева, содержащая поля Имя, Символ и Атомное число. Потенциальные ключи имеют очень большое значение в реляционной теории. Они служат для адресации кортежей. Указав значение потенциального ключа мы гарантированно получим не более одного кортежа. Для отношений, связанных с другими «базовыми» отношениями, существуют еще внешние ключи, использующиеся для установления связи.

· Внешний ключ – это такой атрибут подчиненного отношения, который используется для установления связи с базовым отношением. Он содержит значения, всегда совпадающие с некоторыми значениями потенциального ключа базового отношения.

Исходя их вышеприведенных понятий, математически отношение можно описать следующим образом. Пусть даны n множеств Dl, D2, D3,..., Dn. Тогда отношение R есть множество упорядоченных кортежей<d1, d2, d3 ,..., dn>,где dkÎDk, dk– атрибут, a Dk– домен отношения R.

В середине 70-х годов инженером IBM Коддом (Codd) была предложена модель данных, основанная на математических операциях исчисления отношений и реляционной алгебре. Основной структурной единицей этой модели являлось отношение (relation). Поэтому такая модель данных получила название реляционной. Коддом был также разработан язык манипулирования данных, представленных в виде отношений. Он предложил два эквивалентных между собой по своим выразительным возможностям варианта языка манипулирования данными:

5. Реляционная алгебра. Это процедурный язык, так как отношение, являющееся результатом запроса к реляционной БД, вычисляется при выполнении последовательности реляционных операторов, применяемых к отношениям. Операторы состоят из операндов, в роли которых выступают отношения, и реляционных операций. Результатом реляционной операции является отношение. Операции реляционной алгебры можно разделить на две группы. Первую группу составляют операции над множествами, к которым относятся операции объединения, пересечения, разности, деления и декартова произведения. Вторую группу составляют специальные операции над отношениями: проекция, выборка и соединение.

6. Реляционное исчисление. Это непроцедурный язык описательного или декларативного характера, содержащий лишь информацию о желаемом результате. Процесс получения этого результата скрыт от пользователя. К языкам такого типа относятся SQL и QBE. Первый основан на реляционном исчислении кортежей, второй – на реляционном исчислении доменов.

С помощью этих языков можно извлекать подмножество столбцов и строк таблицы, создавая таблицы меньшей размерности, а также объединять связанные данные из нескольких таблиц, создавая при этом таблицы большей размерности. Следовательно, различные пользователи могут выделять в реляционной БД различные наборы данных и связей между ними. Этот способ представления данных наиболее естественен и обозрим для конечного пользователя. Реляционная модель данных очень гибка, поскольку любое представление данных с некоторой избыточностью можно свести к двумерным таблицам.

Отношения

Теоретическим фундаментом реляционного подхода к БД является математическая теория отношений. Основные понятия и операции над отношениями используются в реляционных БД.

Основные понятия и способы представления отношений. Всякая система (математическая, информационная) непосредственно связана со множеством каких-то объектов, или элементов. Так, в математике используются множества чисел: натуральных, положительных, вещественных и др. В алгебре рассматриваются элементы, которые можно складывать, вычитать, умножать и т.д., а в геометрии — множества точек: прямые, линии, плоскости и т.д. Информационная система объекта, например, учебного заведения, содержит информацию о преподавателях, студентах, кафедрах, факультетах, лабораториях, расписании занятий и т. п.

Помимо элементов система включает в себя связи, отношения между ними. Так, числа а и b могут быть равны (а = b)_, не равны (а ≠ b), а больше или равно b (а ≥ b); фигуры А и В могут быть конгруэнтны (А = В), А может содержать В (A 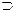B); две прямые А и В могут быть параллельны (А || В), перпендикулярны ( 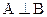). Студент а относится (принадлежит) к множеству А (студенты кафедры).

Все перечисленные отношения касаются двух объектов и поэтому называются бинарными отношениями или просто отношениями. Отношения между тремя объектами называются тернарными, а между n объектами — n-арными. Так, тернарным является отношение между объектами ЗАКАЗЧИК, ПОСТАВЩИК, ТОВАР.

Бинарным отношением R между множествами А и В (обозначается R(A, В)) называется любое множество упорядоченных пар (а, b), где а А, b В. Если (а,b) R, то говорят, что а находится в отношении R к b, и записывают aRb, Поскольку множество упорядоченных пар (а, b), где а A, b В, является декартовым произведением A×В, то бинарным отношением будет любое подмножество этого произведения.

Пример 2.1. Возьмем множество поставщиков и множество предлагаемых товаров. Любое подмножество связей ПОСТАВЩИК — ТОВАР является бинарным отношением.

Пример 2.2. Пусть даны множества A = {1, 2, 3} и В = {2, 3, 4, 5, 6}. Декартово произведение A×В — это множество пар:

(1, 2), (1, 3), …, (1, 6),

(2, 2), (2, 3), …, (2, 6),

(3, 2), (3, 3), …, (3, 6).

Построим бинарное отношение R, у которого первый элемент является делителем второго. Получим следующее бинарное отношение: R={(1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 2), (2, 4), (2, 6), (3, 3), (3,6)}.

Пример 2.3. Пусть Ольга (О), Павел (П), Иван (И) — имена детей в семье. Отношением а — брат b будет:

R = {(П, О), (И, О), (П, И), (И, П)}.

В отношении R(A, В) множество А, т.е. совокупность всех первых координат, называют областью определения отношения R, а множество B, т. е. множество всех вторых координат, — областью его значений. Так, для примера 3.3 область определения — множество {П, И}, а область значений— множество {О, П, И}.

Дополнением к бинарному отношению R будем называть отношение 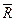, которое определяет подмножество

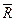= (A×B)\R,

т.е. a 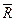b тогда и только тогда, когда {a, b) R. Так, для примера 2.2

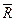= {(2, 3), (2, 5), (3, 2), (3, 4), (3, 5)}.

Бинарные отношения можно задавать различными способами: матрицами, графами, таблицами (сечениями). Отношение R(A, В), где А = {а_1, а₂, ..., a_m}; B = {b_1, b₂, ..., b_n}, можно представить матрицей смежностей, строки которой соответствуют элементам A, а столбцы — элементам В; на пересечении а_i-й строки и b_j-го столбца записана 1, если a_iRb_j, и 0, если a_iRb_j. Матрицы смежности для отношений R и 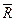для примера 2.2 имеют вид

R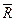

Бинарное отношение R(A, В) можно представить в виде ориентированного графа. Элементы множества А и В — вершины графа, причем ребром соединяются те и только те элементы а А, b В, для которых (a, b) R. Так, в виде графа на рис. 2.10 представлено отношение для примера:

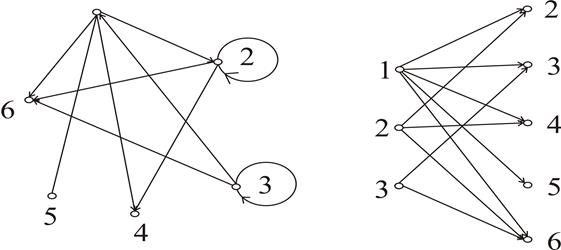
Рис. 2.10. Представление отношения R в виде графа

Пусть даны три множества А, В, С и два отношения R(A, В) и S(B, С). Композицией, или умножением, отношений R и S называют бинарное отношение RS (или R*S) между элементами множеств А и С такое, что aRSc тогда и только тогда, когда существует хотя бы один элемент b В, при котором истинны aRb и bSc.

Пример 2.4. Рассмотрим множества

А = {а_1, а₂, а₃}, В = {b₁, b₂, b₃}, С = {с₁, c₂, c₃, c₄}

и отношения

R (A, B) = {(a₁, b₂), (a₂, b₁), (a₂, b₃), (a₃, b₄)},

S (B, C) = {(b₁, c₂), (b₂, c₁)}.

Умножение отношений RS можно представить в виде графа (рис. 2.11.).

Умножение бинарных отношений ассоциативно, т. е. (RS)T = R(ST). Пусть даны отношения R(A, В), S(B, С) и Т (С, D). Тогда a(RS)Td = aR(ST)d, т.е. элемент а A тогда и только тогда находится в каждом из отношений (RS)T и R(ST) к элементу d D, когда существуют такие элементы b В и c С, что aRb, bSc, cTd. Умножение отношений, однако, не является в общем случае коммутативным (перестановочным), т.е. RS≠SR. Эта операция имеет место только в частных случаях (в этом случае говорят, что R и S перестановочны).

Пример2.5. Пусть даны множества

A = {a, b}, B = {a, b, c}, C = {b, c}

и отношения R (A, В) = {(а, b), (b, с)}, S (B, C) = {(b, с), (а, b)}. Тогда aRSc = aSRc для любых а А и c С.

Умножение k отношений R на множестве H, т.е. k-я степень R, обозначаемая R^k, рекурсивно определяется следующим образом:

1) aR^lb истинно, когда истинно aRb;

2) aRⁱb для i >0 истинно, когда существует такое с А,
что aRc и cR^i-lb истинны.

Пусть имеем aR³b. Тогда существует такое с_1, что aRc₁ и c₁R²b. Для c₁R²b найдется такое с₂, что c₁Rc₂ и c₂Rb_, т. е. для аR³b есть такое с_1, с₂ А, что аRс₁, c₁Rc₂ и с₂Rb.

Пусть в одном или нескольких множествах даны от­ношения R_i (i пробегает множество индексов I) и S.Тогда

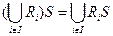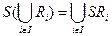, (2.1)

Согласно a[(UR_i)S]с существует такой элемент b, что a( 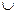Ri)b и bSc. А это, в свою очередь, равносильно существованию такого индекса i₀, что a R 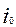b и bSc, т.е.

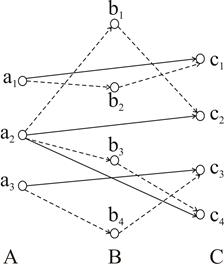
Рис. 2.11.Представление операции умножения отношений RS в виде графа

a(R 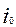S) c и поэтому a( 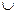R_iS)c. Заметим, что в равенствах (3.1) объединение нельзя заменить пересечением. Из (3.1) следует, что если даны отношения R, R' и S, причем R 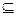R',то

RS 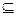R'S, SR 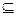SR'.(2.2)

Действительно, так как R 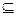R’ то R 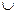R' = R', что приводит к равенству (R 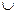R’) S = RS 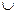R’S = R’S, которое равносильно включению 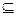RS R'S.

Функциональные отношения, отображения.Пусть r(a, b) — элемент отношения R(A, В). Проекцией элемента r на множество А является элемент а. Проекцией отношения R(A, В) на множество А называется множество элементов а М, которые являются проекциями элементов r R на А. Сечением отношения R(A, В) по элементу аназывается множество элементов b_i B, для которых (a,b_i) R.

Множество сечений по элементам а А отношения R (A, В) называется фактор-множеством множества В по отношению R и обозначается B/R. Таблица, в которой под каждым элементом а_i А расположено соответствующее ему сечение, полностью определяет отношение R(A, В); вторая строка таблицы является фактор-множеством B/R:

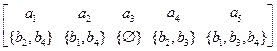
Сечение R(X) пo X 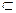A есть объединение сечений R(x) по х Х. Таким образом, R(X) B и для нашего примера

R(a₂, а₄)= {b_1, b₂, b₃,b₄}.

Отношение R (А, В) называется функциональным, если для каждого а А существует не более одного b В, удовлетворяющего отношению aRb (рис. 2.12).

Отношение R(A, В) называется взаимно однозначным, если для функционального отношения R симметричное ему отношение тоже функционально.

Всякому отношению R(A, В) можно поставить в соответствие функцию f(x), если его сечение по каждому х А либо пусто, либо есть элемент множества В. Если f(x) всюду определена, т. е. область определения функции совпадает с А, то говорят, что отношение R(A, В) есть отображение множества А в В. Функциональное отношение R(A, В) вызывается отображением А в В, если для каждого а A существует один и только один элемент

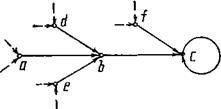
Рис. 2.12. Представление функционального отношения R(A, В) в виде графа

b B, удовлетворяющий отношению aRb. Элемент b называется образом элемента а и обозначается aR, а элемент а — прообразом элемента b при отображении R. Совокупность всех прообразов элемента b в А при отображении R называется полным прообразом этого элемента в А.

Отображение можно задавать таблицей, состоящей из двух строк. В верхней строке записываются элементы а 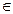А, а под ними — соответствующие названным элементам прообразы из множества В. Например, таблица

R =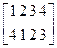

определяет отображение множества {1, 2, 3, 4} в множество {2, 5, 1, 4}. При этом 1R = 2, 2R = 5, 3R=1, 4R = 4.

Пусть Р — отображение А в В, Q — отображение В в С. Умножение отображения PQ будет отображением А в С, и для любого x?А справедливо x(PQ) = (xP)Q. Действительно, пусть x(PQ)=c. Тогда для некоторого у 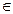В имеем хРу и yQc, откуда хР = у и поэтому с = (xP)Q. Обратно, из (xP)Q следует x(PQ).

Умножение отображений, заданных таблицами, покажем на примере:

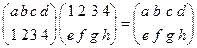
Отображение R называют сюръективным (сюръекцией) или отображением множества А на множество В, когда каждый элемент b?В имеет хотя бы один прообраз из А.

Пример 2.6. Пусть А и В — множества вещественных чисел. Отображением (сюръективным) А на В может быть функция, определенная формулой х → Зх + 5, т. е. х переходит в y = 3x + 5.

Функция х→у=х² определяет отображение множества A в Б, которое не является сюръективным, так как отрицательные числа из В не являются образами элементов из А.

Отображение R множества А в множество В называется взаимно однозначным, если обратное отношение R^-l есть отображение В в А. Для взаимно однозначного отображения, заданного с помощью сечений, необходимо и достаточно, чтобы каждый элемент из В встречался в нижней строке таблицы один и только один раз. Так, три таблицы, приведенные ранее в качестве примера умножения отображений, соответствуют взаимно однозначным отображениям.

Взаимно однозначное отображение, для которого R всюду определено, называют инъективным (инъекцией).

Пример 2.7. Пусть А — множество действительных чисел, В — множество положительных действительных чисел. Отображение х→у = е^х является взаимно однозначным, так как каждому у соответствует х = ln y. Таким образом, имеем инъективное отображение, обратным для которого будет отображение у→х=ln y.

Взаимно однозначное отображение R между элементами одного множества, для которого R и R^-l всюду определены, называется отображением на себя или биективным отображением. Биективное отображение является одновременно сюръективным и ииъективным.

При отображении некоторого множества самого в себя говорят, что отображение aRb переводит точку а в точку b. При aRa точку а называют неподвижной точкой отображения R. Если все точки множества A при отображении неподвижны, то отображение называют тождественным и обозначают Е_А. Очевидно, что Е^-1=Е и для любого отображения R RE=ER = R. При задании отображения в себя с помощью сечений в нижней строке таблицы будут такие же элементы, как и в верхней (возможно, в другом порядке), и каждый из них встречается один и только один раз:

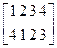
Матрица смежностей, соответствующая отображению в себя, является квадратной:

Представление отображения в себя в виде графа состоит из циклов (конечных или бесконечных).