ПРАКТИЧЕСКАЯ РАБОТА. ДЕЙСТВИЯ НАД ПОЛОЖИТЕЛЬНЫМИ ДЕЙСТВИТЕЛЬНЫМИ ЧИСЛАМИ
Цель. Уметь выполнять различные тождественные преобразования над положительными действительными числами
Теоретическая часть
Вопросы к изучению
1. Понятие дроби.
2. Положительные рациональные числа.
3. Запись положительных рациональных чисел в виде десятичных дробей.
4. Действительные числа.
Основные понятия темы
Ø дробь (правильная и неправильная);
Ø равные дроби;
Ø несократимая дробь;
Ø положительное рациональное число;
Ø равенство положительных рациональных чисел;
Ø смешанная дробь;
Ø десятичная дробь;
Ø бесконечная периодическая десятичная дробь;
Ø бесконечная непериодическая десятичная дробь;
Ø иррациональное число;
Ø действительное число.
Замечания, выводы
· Отношение равенства дробей есть отношение эквивалентности и воспользовавшись этим определяют понятие положительного рационального числа.
· Сложение и умножение положительных рациональных чисел связано с измерением длин отрезков; получены формулы для нахождения их суммы и произведения.
· Определение отношения «меньше» на множестве Q+ позволило назвать его основные свойства: оно упорядоченное, плотное, в нем нет наименьшего и наибольшего числа.
· Доказано, что множество Q+ положительных рациональных чисел удовлетворяет всем тем условиям, которые позволяют его считать расширением множества N натуральных чисел.
· Введя десятичные дроби доказано, что любое положительное рациональное число представимо бесконечной периодической десятичной дробью.
· Бесконечные непериодические дроби считают записями иррациональных чисел.
· Если объединить множества положительных рациональных и иррациональных чисел, то получаем множество положительных действительных чисел: Q+ÇJ+ = R+
· Если к положительным действительным числам присоединить отрицательные действительные числа и нуль, то получаем множество R всех действительных чисел.
Обязательные задания
1. Известно, что длина отрезка х при единичном отрезке b выражается дробью 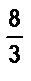 . Как могла получиться такая дробь при измерении длины отрезка х? Существуют ли другие дроби, выражающие длину отрезка х при том же единичном отрезке е?
. Как могла получиться такая дробь при измерении длины отрезка х? Существуют ли другие дроби, выражающие длину отрезка х при том же единичном отрезке е?
2. Выберите единицу длины и постройте отрезок, длина которого выражается дробью: а) 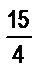 ; б)
; б) 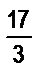 ; в)
; в) 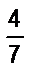 .
.
3. Как установить, равны ли дроби: а) 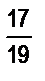 и
и 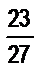 ; б)
; б) 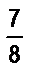 и
и 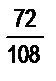 .
.
4. На множестве дробей 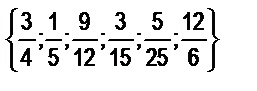 отношение равенства. Постройте граф этого отношения. Каковы особенности этого графа? С чем они связаны?
отношение равенства. Постройте граф этого отношения. Каковы особенности этого графа? С чем они связаны?
5. Приведите дроби к наименьшему общему знаменателю: а) 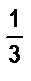 и
и 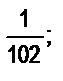
б) 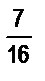 и
и 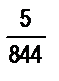 ; в)
; в) 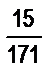 и
и 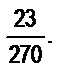
6. Найдите несократимую дробь, равную следующей: а) 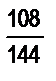 ; б)
; б) 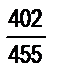 ; в)
; в) 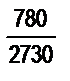 ; г)
; г) 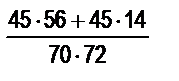 ; д)
; д) 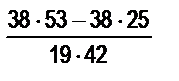 .
.
7. Рациональное число представлено дробью 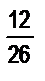 . Может ли оно быть представлено дробью
. Может ли оно быть представлено дробью 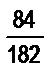 ? А дробью
? А дробью 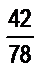 ?
?
8. Какие из следующих дробей несократимые: а) 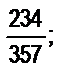 б)
б) 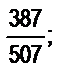 в)
в) 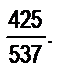
9. Вычислите значения следующих выражений, записав их в виде несократимых дробей; выполненные преобразования обоснуйте: а) 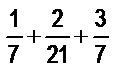 ; б)
; б) 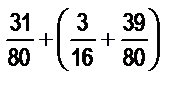 ; в)
; в) 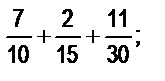 г)
г) 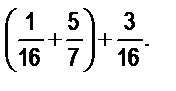
10. Вычислите значения следующих выражений, записав их в виде несократимых дробей; выполненные преобразования обоснуйте: а) 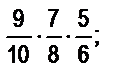 б)
б) 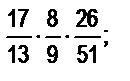 в)
в) 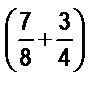
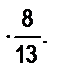
11. Сравните числа: а) 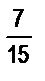 и
и 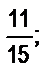 б)
б) 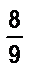 и
и 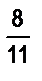 ; в)
; в) 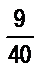 и
и 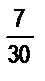 ;
;
г) 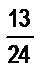 и
и 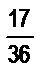 .
.
12. Найдите три дроби, которые заключены между дробями 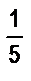 и
и 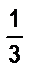 .
.
13. Найдите значение следующих выражений: а) 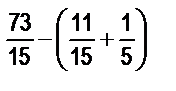 ;
;
б) 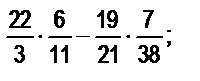 в)
в) 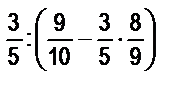 .
.
14. Выполните указанные действия и найдите значение выражения: 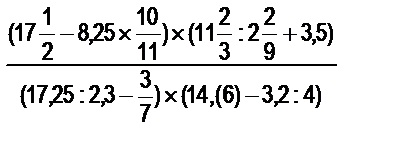
15. Какие из данных чисел являются дробными: а) 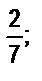 б)
б) 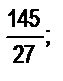 в)
в) 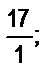 г)
г) 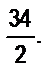
16. Число 2 умножили на правильную дробь. Какое число получилось - больше или меньше числа 2? А если 2 умножить на неправильную дробь?
17. Может ли при умножении числа 3 на правильную дробь получиться число: а) меньше 1; б) больше 1?
18. Запишите дроби 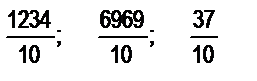 в виде десятичных.
в виде десятичных.
19. Запишите числа 7,11; 0,45; 13,745 в виде несократимых обыкновенных дробей.
20. Какими будут численные значения следующих величин, если в качестве единицы длины взять 1 м: а) 23 см 2 мм; б) 90 дм 16 см 8 мм; в) 5м 17дм; г) 1км 120м?
21. Выразите в килограммах: а) 1,52 т; б) 0,38 т; в) 13,6 г; г) 426,5 г.
22. Выразите в квадратных сантиметрах: а) 3,548дм2; б) 3,9 м2; в) 635мм2.
23. Сформулируйте правила сложения и вычитания десятичных дробей; выполните действия: а) 8,23+3,568; б) 7,395-6,27; в) 12,364+17,729; г) 15,36-9,68.
24. Сформулируйте правило умножения двух десятичных дробей и объясните, почему в произведении запятой отделяют столько последних цифр, сколько их отделено в первом и втором множителях вместе.
25. Сформулируйте правило деления десятичных дробей; проиллюстрируйте его на примере деления числа 4,62 на 0,2.
26. Расстояние от Земли до Солнца 150 млн. км. Скорость света 300тыс.км/с. За сколько минут луч Солнца достигнет Земли?
27. Вычислите наиболее простым способом:
а) 49,5+2,738- 6,856+(7,956-2,638); б) 4,3-3,5+1,44:3,6+3,6:1,44×(0,1-0,02).
28. Не выполняя вычислений, сравните следующие произведения: а)19,91×199,2 и 1,991×1992; б)1,992×199,3 и 1,992×1993.
29. Что больше: 35% от 40 или 40% от 35?
30. Увеличьте число: а) 60 на 10%; б) 80 на 2,5%.
31. Число х увеличили на 45%. Во сколько раз увеличили число?
32. Число х увеличили в 2,4 раза. На сколько процентов увеличили число?
33. Туристы прошли 75% маршрута и им осталось пройти еще 5,5 км. Какова длина маршрута?
34. Какие из следующих чисел можно записать в виде конечных десятичных дробей: а) 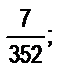 б)
б) 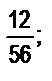 в)
в) 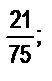 г)
г) 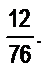
35. Следующие обыкновенные дроби запишите в виде десятичных: а) 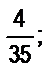 б)
б) 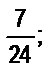 в)
в) 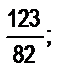 г)
г) 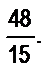
Творческие задания
1. Докажите, что отношение «меньше» на множестве Q+ является отношением порядка.
2. Решите задачи арифметическим способом.
а) Прямоугольник разделили на 8 равных частей. Сначала закрасили 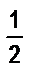 прямоугольника, потом
прямоугольника, потом 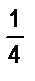 , затем
, затем 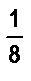 . Весь ли прямоугольник закрасили?
. Весь ли прямоугольник закрасили?
б) Мальчик отпил 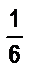 чашки черного кофе и долил молока, затем
чашки черного кофе и долил молока, затем 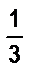 отпил чашки и опять долил молока, потом отпил еще
отпил чашки и опять долил молока, потом отпил еще 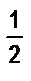 чашки и снова долил молока. Наконец, он допил кофе с молоком. Чего больше выпил мальчик - кофе или молока?
чашки и снова долил молока. Наконец, он допил кофе с молоком. Чего больше выпил мальчик - кофе или молока?
3. Решите арифметическим методом задачи.
а) В трех гаражах помещается 460 машин. Число машин в первом гараже составляет 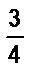 числа машин, помещающихся во втором, а в третьем гараже в
числа машин, помещающихся во втором, а в третьем гараже в 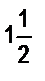 раза больше машин, чем в первом. Сколько машин в каждом гараже?
раза больше машин, чем в первом. Сколько машин в каждом гараже?
б) Из двух пунктов, расстояние между которыми 25 км, вышли одновременно навстречу друг другу два пешехода. Один из них проходил в час на 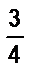 км больше другого. С какой скоростью шел каждый, если через 2 ч после выхода расстояние между ними стало
км больше другого. С какой скоростью шел каждый, если через 2 ч после выхода расстояние между ними стало 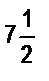 км?
км?
в) Двум машинисткам было поручено перепечатать рукопись. Первая машинистка перепечатала 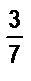 всей рукописи, а вторая -
всей рукописи, а вторая - 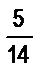 всей рукописи. Сколько страниц в рукописи, если первая машинистка перепечатала на 7 страниц больше, чем вторая?
всей рукописи. Сколько страниц в рукописи, если первая машинистка перепечатала на 7 страниц больше, чем вторая?
4. Решите задачи арифметическим методом.
а) Турист прошел в первый день 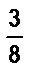 всего маршрута, во второй день 40 % остатка, после чего ему осталось пройти на 6,5 км больше, чем он прошел во второй день? Какова длина маршрута?
всего маршрута, во второй день 40 % остатка, после чего ему осталось пройти на 6,5 км больше, чем он прошел во второй день? Какова длина маршрута?
б) На уборке улицы работают две машины. Первая из них может убрать всю улицу за 40 мин, второй для этого требуется 75% времени первой. Обе машины начали работу одновременно. После совместной работы в течение 0,25 часа вторая машина прекратила работу. За сколько времени после этого первая машина закончила уборку улицы?
5. Известно, что любое положительное рациональное число можно изобразить точкой на координатном луче. Исчерпывают ли точки с положительными рациональными координатами весь координатный луч?
6. Опишите процесс измерения длины отрезка, если отчет о нем представляется дробью: а) 3,46; б) 3,(7); в) 3,2(6).
7. Седьмая часть единичного отрезка укладывается в отрезке а 13 раз. Конечной или бесконечной дробью будет представлена длина этого отрезка? Периодической или непериодической?
8. Дано множество: {7; 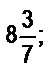
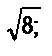 35,91; - 12,5; -
35,91; - 12,5; - 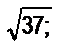 0; 0,123; 4136}. Можно ли разбить его на два класса: рациональные и иррациональные?
0; 0,123; 4136}. Можно ли разбить его на два класса: рациональные и иррациональные?
ВОПРОСЫ К КОЛЛОКВИУМУ
1. Из истории возникновения понятия натурального числа.
2. Порядковые и количественные натуральные числа. Счет.
3. Теоретико-множественный смысл количественного натурального числа и нуля.
Дата добавления: 2021-01-26; просмотров: 996;











