Обобщением различных случаев деления целого неотрицательного числа а на натуральное число b является следующий алгоритм деления уголком.

1. Если а =b, то частное q = 1, остаток r = 0.

2. Если а>b и число разрядов в числах а и b одинаково, то частное q находим перебором, последовательно умножая b на 1, 2, 3, 4, 5, 6, 7, 8, 9, так как а<10b. Этот перебор можно ускорить, выполнив деление с остатком цифр старших разрядов чисел а и b .

3. Если а>b и число разрядов в числе а больше, чем в числе b, то записываем делимое а и справа от него делитель b, который отделяем от а уголком и ведем поиск частного и остатка в такой последовательности:

а) Выделяем в числе а столько старших разрядов, сколько разрядов в числе b или, если необходимо, на один разряд больше, но так, чтобы они образовывали число d₁, больше или равное b . Перебором находим частное q₁ чисел d₁, и b, последовательно умножая b на 1, 2, 3, 4, 5, 6, 7, 8, 9. Записываем q₁ под уголком (ниже b).

б) Умножаем b на q₁, и записываем произведение под числом а так, чтобы младший разряд числа bq₁ был написан под младшим разрядом выделенного числа d₁.

в) Проводим черту под bq₁ и находим разность r₁ = d₁ - bq₁.

г) Записываем разность r₁, под числом bq₁ , приписываем справа к r₁ старший разряд из неиспользованных разрядов делимого а и сравни­ваем полученное число d₂ с числом b .

д) Если полученное число d₂ больше или равно b, то относительно него поступаем согласно п. 1 или п. 2. Частное q₂ записываем после q₁.

е) Если полученное число d₂ меньше b, то приписываем еще столько следующих разрядов, сколько необходимо, чтобы получить первое число d₃, большее или равное b. В этом случае записываем после q₁ то же число нулей. Затем относительно d₃ поступаем согласно пп. 1, 2. Частное q₂ записываем после нулей. Если при использовании младшего разряда числа а окажется, что d₃ < b, то тогда частное чисел d₃ и b равно нулю, и этот нуль записывается последним разрядом в частном, а остаток r = d₃.

ПРАКТИЧЕСКАЯ РАБОТА. АЛГОРИТМЫ АРИФМЕТИЧЕСКИХ ДЕЙСТВИЙ

Цель. Показать на практических примерах использование алгоритмов действий сложения, умножения, вычитания и деления над натуральными числами. Уметь обосновать каждый шаг алгоритмов при выполнении практических заданий и решении текстовых задач из курса начальной школы.

Теоретическая часть

Вопросы к изучению

1. Запись числа в десятичной системе счисления

2. Алгоритм сложения

3. Алгоритм вычитания

4. Теоретические основы алгоритмов умножения и деления

5. Алгоритмы умножения и деления

Основные понятия темы

Ø Десятичная запись натурального числа – это его представление в виде

х = а_n × 10 ⁿ + а _{n – 1} × 10 ^{n – 1} + …+ а₁ × 10 + а₀ = , где а_n,а _n–1,…,а₁,а₀ принимает значения 0,1,2,3,4,5,6,7,8,9, и а _n¹ 0.

- В таком виде можно записать любое натуральное число и запись эта единственная.

- Десятичная запись натуральных чисел позволяет их сравнивать и выполнять, по определенным правилам (алгоритмам), над ними действия.

- В основе алгоритма сложения многозначных чисел лежат следующие теоретические факты:

- способ записи чисел в десятичной системе счисления;

- свойства коммутативности и ассоциативности сложения;

- дистрибутивность умножения относительно сложения;

- таблица сложения однозначных чисел.

Ø В общем виде алгоритм сложения натуральных чисел, записанных в десятичной системе счисления, формулируют так:

1. Записывают второе слагаемое под первым так, чтобы соответствующие разряды находилось друг под другом.

2. Складывают единицы первого разряда. Если сумма меньше десяти записывают ее в разряд единиц ответа и переходят к следующему разряду (десятков).

3. Если сумма единиц больше или равна десяти, то представляют ее в виде а₀+b₀=1·10+с₀, где с₀ - однозначное число; записывают с₀, в разряд единиц ответа и прибавляют 1 к десяткам первого слагаемого, после чего переходят к разряду десятков.

4. Повторяют те же действия с десятками, потом с сотнями и процесс заканчивается, когда оказываются сложенными цифры старших разрядов. При этом, если их сумма больше или равна десяти, то приписываем впереди обоих слагаемых нули, увеличиваем нуль перед первым слагаемым на 1 и выполняем сложение 1 + 0 = 1.

Ø Вычитание многозначного числа из многозначного основывается на:

– способе записи числа в десятичной системе счисления;

– правилах вычитания числа из суммы и суммы из числа;

– свойстве дистрибутивности умножения относительно вычитания;

– таблице сложения однозначных чисел.

Ø В общем виде алгоритм вычитания чисел в десятичной системе счисления следующий:

1. Записываем вычитаемое под уменьшаемым так, чтобы соответствующие разряды находились друг под другом.

2. Если цифра в разряде единиц вычитаемого не превосходит соответствующей цифры уменьшаемого, вычитаем ее из цифры уменьшаемого, записываем разность в разряд единиц искомого числа, после чего переходим к следующему разряду.

3. Если же цифра единиц вычитаемого больше единиц уменьшае­мого, т.е. b₀ > а₀, а цифра десятков уменьшаемого отлична от нуля, то уменьшаем цифру десятков уменьшаемого на 1, одновременно увеличив цифру единиц уменьшаемого на 10, после чего вычитаем из числа 10 + а₀ число b₀ и записываем разность в разряде единиц ис­комого числа, далее переходим к следующему разряду.

4. Если цифра единиц вычитаемого больше цифры единиц уменьшаемого, стоящие в разряде десятков, сотен и т.д. уменьшаемого, равны нулю, то берем первую отличную от нуля цифру в уменьшаемом (после разряда единиц), уменьшаем ее на 1, все цифры в младших разрядах до разряда десятков включительно увеличиваем на 9, а цифру в разряде единиц на 10: вычитаем b₀ из 10 + а₀ , записываем разность в разряде единиц искомого числа и переходим к следующему разряду.

5. В следующем разряде повторяем описанный процесс.

6. Вычитание заканчивается, когда производится вычитание из старшего разряда уменьшаемого.

Ø Теоретической основой алгоритма умножения многозначного числа на многозначное являются:

- запись чисел в десятичной системе счисления;

- свойства сложения и умножения;

- знание таблиц сложения и умножения однозначных чисел.

Ø Общий вид алгоритма умножения числа х = на число у = :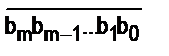

1. Записываем множитель х под ним второй множитель у.

2. Умножаем число х на младший разряд b₀ числа у и записываем произведение х × b₀ под числом у.

3. Умножаем число х на следующий разряд b₁ числа у и записываем произведение х × b₁, но со сдвигом на один разряд влево, что соот­ветствует умножению х × b₁ на 10.

4. Продолжаем вычисление произведений до вычисления х × b_k.

5. Полученные k + 1 произведения складываем.

Ø Теоретической основой алгоритма деления целого неотрицательного числа на натуральное число является:

- действие деления с остатком.

Ø Алгоритмом деления уголком целого неотрицательного числа а на натуральное число b является следующий:

1.Если а = b, то частное q = 1, остаток r = 0.

2.Если а > b и число разрядов в числах а и b одинаково, то частное q находим перебором, последовательно умножая b на 1, 2, 3, 4, 5, 6, 7, 8,9, так как а < 10 b. Этот перебор можно ускорить, выполнив деление с остатком цифр старших разрядов чисел а и b .

3.Если а > b и число разрядов в числе а больше, чем в числе b, то записываем делимое а и справа от него делитель b, который отделяем от а уголком и ведем поиск частного и остатка в такой последова­тельности:

а) Выделяем в числе а столько старших разрядов, сколько разрядов в числе b или, если необходимо, на один разряд больше, но так, чтобы они образовывали число d₁, больше или равное b . Перебором нахо­дим частное q₁ чисел d₁, и b, последовательно умножая b на 1, 2, 3, 4, 5, 6, 7, 8, 9. Записываем q₁ под уголком (ниже b).

б) Умножаем b на q₁, и записываем произведение под числом а так, чтобы младший разряд числа bq₁ был написан под младшим разрядом выделенного числа d₁.

в) Проводим черту под bq₁ и находим разность r₁ = d₁ - bq₁.

г) Записываем разность r₁, под числом bq₁ , приписываем справа к r₁ старший разряд из неиспользованных разрядов делимого а и сравниваем полученное число d₂ с числом b .

д) Если полученное число d₂ больше или равно b, то относительно него поступаем согласно п. 1 или п. 2. Частное q₂ записываем после q₁.

е) Если полученное число d₂ меньше b, то приписываем еще столько следующих разрядов, сколько необходимо, чтобы получить первое число d₃, большее или равное b. В этом случае записываем после q₁ то же число нулей. Затем относительно d₃ поступаем согласно пп. 1, 2. Частное q₂ записываем после нулей. Если при использовании младшего разряда числа а окажется, что d₃ < b, то тогда частное чисел d₃ и b равно нулю, и этот нуль записывается последним разрядом в частном, а остаток r = d₃.

Практическая часть

1. На примере сложения чисел 237 и 526 покажите, какие теоретические факты лежат в основе алгоритма сложения многозначных чисел.

2. При изучении алгоритма сложения трехзначных чисел в начальной школе последовательно рассматриваются такие случаи сложения: 231 + 342; 425 + 135; 237 + 526; 529 + 299. Каковы особенности каждого из этих случаев?

3. Вычислите устно значение выражение; использованный прием обоснуйте:

а) 2746 + 7254 + 9876; б) 7238+8978+2768;

в) (4729 + 8473) + 5271; г) 4232 + 7419 + 5768 + 2591;

д) (357 + 768 + 589) + (332 + 211 + 643).

4. Какие рассуждения школьников вы будете считать правильными при выполнении задания.

а) Можно ли утверждать, что значения сумм в каждом столбике одинаковы:

2459+121 53075+2306

2458+122 53076+2305

2457+123 53006+2375

2456 + 124 53306+2075

б) Можно ли записать значения этих сумм в порядке возрастания: 4583+321 4593+311 4573+331

5. На примере нахождения разности чисел 469 и 246, 757 и 208 проиллюстрируйте теоретические основы алгоритма вычитания чисел столбиком.

6. Выполните вычитание, используя запись и объясняя каждый шаг алгоритма: а)84072 - 63894; б)940235-32849; в)935204 - 326435; г) 653481 - 233694.

7. Сколько пятизначных чисел можно записать, используя цифры 1 и 0? Чему равна разность между наибольшим и наименьшим из этих пятизначных чисел?

8. Назовите способы проверки правильности вычитания многозначных чисел и дайте им обоснование.

9. Вычислите (устно) значение выражения, использованные приемы обоснуйте: а)2362-(839+1362); б)(1241+576)-841 в)(7929+5027+4843)-(2027+3843).

10. На примере умножения числа 357 на 4 проиллюстрируйте теоретические основы алгоритма умножения многозначного числа на однозначное.

11. На примере умножения 452 на 186 проиллюстрируйте теоретические основы алгоритма умножения многозначного числа на многозначное.

12. Решение задачи запишите в виде числового выражения, а затем найдите его значение:

а) На элеватор отвезли 472 т овса, ржи на 236 т больше, чем овса, пшеницы в 4 раза больше, чем овса и ржи вместе. Сколько тонн пшеницы отвезли на элеватор?

б) Столяр делает в день 18 рам, а его помощник на 4 рамы меньше. Сколько рам они сделают за 24 дня, если каждый день будут работать, вместе?

13. Как могут рассуждать учащиеся, выполняя следующее задание: «Ширина земельного участка прямоугольной формы равна 24 м. Это в 6 раз меньше его длины. Объясни, что обозначают выражения, записанные по условию задачи, и вычисли их значения: 24× 6; 24× (24 × 6); (24 + 24 × 6) × 6; 24 × 2; 24 × 2 + 24 × 6 × 2».

14. Выполните умножение чисел, используя запись столбиком, и объясняя каждый шаг алгоритма: а) 984 × 27; б)7040 × 234; в)8276 × 73; г)4569 × 357.

15. Используя свойства умножения, найдите наиболее рациональ­ным способом значение выражения:

а) 8 × 13 × 4 × 125 × 25; г)124× 4 + 116× 4;

б) 24×(27×125); д) (3750-125) ×8;

в) (88 + 48) ×125; е)1779×1243 – 779×1243.

16. Зная, что 650×34 = 22100, найдите произведение чисел, не выполняя умножения столбиком: а) 650×36; б)650×32; в) 649×34.

17. Найдите и обоснуйте приемы умножения 24 на 35 и, пользуясь ими, умножьте на 35 числа: 12, 18, 24, 32, 48, 64.

18. Вычислите рациональным способом значение выражения:

а) (420-394) × 405 – 25 × 405; б) 105 × 209 + (964 - 859) × 209 × 400.

19. Найдите значения выражений 13 ×11, 27 ×11, 35 ×11, 43 ×11, 54 ×11. Верно ли: чтобы найти результат умножения двузначного числа на 11 в случае, когда сумма цифр двузначного числа меньше 10, достаточно между цифрами данного числа написать число, равное сумме его цифр?

20. Найдите значение выражений 29 × 11, 37 × 11, 47 × 11, 85×11, 97 × 11. Верно ли: чтобы найти результат умножения двузначного числа на 11 в случае, когда сумма цифр двузначного числа больше или равна 10, достаточно между цифрой десятков, увеличенной на 1, и цифрой единиц написать число, равное разности между суммой его цифр и чис­лом 10?

21. Не выполняя деления, определите число цифр частного чисел:

а) 486 и 7; б) 7243 и 238;в) 5792 и 27; г) 43126 и 543.

22. На примере деления числа 867 на 3 проиллюстрируйте теоретические основы алгоритма деления трехзначного числа на однозначное.

23. Обоснуйте процесс деления уголком а на b , если а) а = 4066, b = 38; б) а = 4816, b = 112.

24. Как, не вычисляя, можно установить, что деление выполнено неправильно, если: а) 51 054:127 = 42; б) 405945:135 = 307?

25. Не вычисляя значений выражений, поставьте знаки > или <, чтобы получились верные неравенства.

а) 1834:7 … 783:9; б) 8554:91 ...7488:72; в) 137532:146 ... 253242:198; г) 7248:6 ...758547:801.

26. Не производя деления, разбейте данное выражение на классы при помощи отношения «иметь в частном одно и тоже число цифр»: а)20700:300; б)20300:700; в) 5460:60; г) 14 640 : 80; д) 30 720:40; е) 1500:300.

27. Решение задачи запишите в виде числового выражения, а затем найдите его значение.

а) Туристы совершили экскурсию по реке на катере, проплыв всего 66 км. Сначала 2 ч они плыли со скоростью 18 км/ч, а остальной путь - со скоростью 15 км/ч. Сколько всего часов находились в пути туристы?

б) Печенье упаковали в пачки по 250 г. Пачки сложили в ящик в 4 слоя. Каждый слой имеет 5 рядов по 6 пачек в каждом. Определите массу сложенного в ящик печенья.

28. Найдите значение первого выражения, а затем используйте его при вычислении значения второго.

а) 45120: (376×12), б) 241×(1264:8), в) 45120: (376×3); г) 241×(1264:4).

29. Найдите двумя способами значение выражения: а) (297+405+567):27; б) 56×(378:14); в) (240×23); 48; г) 15120:(14×5×18).

30. Найдите значение выражения:

а) 8919:9+114240:21 б)1190-35360:34+271;

в) 8631-(99+44 352:63) г) 48 600×(5 045-2 040): 243- (86043:43 +504) ×200;

д) 4880×(546+534): 122-6390×(8 004-6924) ×213.

Творческие задания

1. Докажите, что а + (b – с) =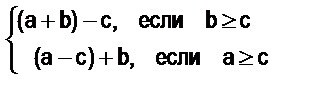

2. Используя это правило, вычислите значение выражения:

а) 6420+(3580-1736); б) 5480 + (6290 - 3480).

3. Докажите, что а – ( b - с) =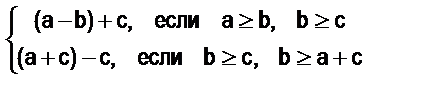

4. Используя это правило, вычислите значение выражения: а) 3720-(1742-2678), б) 2354-(965-1246).

5. Докажите, что (а – в) – с =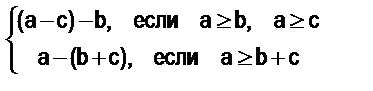

6. Используя это правило, вычислите значение выражения: а) (4317-1928)-317; б) (5243-1354)-1646.

7. Объясните, почему нижеприведенные задачи решаются при помощи умножения чисел и решите их.

а) Земля при обращении вокруг Солнца за сутки проходит примерно 2 505 624 км. Какой путь проходит Земля за 365 дней?

б) В школу привезли 56 пачек книг, по 24 книги в каждой пачке. Сколько всего книг привезли в школу?

8. Объясните, почему следующие задачи решаются при помощи деления чисел, и решите их.

а) В 125 коробок разложили поровну 3000 карандашей. Сколько карандашей в каждой коробке?

б) Расфасовали 12 кг 600 г конфет в коробки по 300 г в каждой. Сколько коробок конфет получилось?