Определение коэффициентов аппроксимирующей функции
При определении коэффициентов широко используют метод выбранных точек, в соответствии с которым значения коэффициентов определяют исходя из совпадения значений функции со значениями аппроксимирующей функцией в ряде заранее выбранных точек, называемых узлами интерполяции.
Если при аппроксимации ВАХ, задаваемой множеством точек 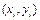 выбрана функция:
выбрана функция:
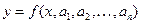 , (19)
, (19)
имеющая 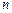 неизвестных коэффициентов
неизвестных коэффициентов 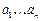 , то для определения этих коэффициентов выбирают
, то для определения этих коэффициентов выбирают 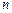 наиболее характерных точек, лежащих в пределах рабочей области.
наиболее характерных точек, лежащих в пределах рабочей области.
Подставляя в уравнение (19) выбранные значения 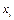 ,
, 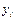 , получают систему из
, получают систему из 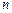 -уравнений
-уравнений 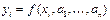 , решение которой дает искомые коэффициенты
, решение которой дает искомые коэффициенты 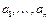 .
.
Очевидно, найденные коэффициенты обеспечивают совпадение значений заданной и аппроксимирующей функции в узлах интерполяции, однако в промежутках между ними погрешность аппроксимации может быть весьма существенной.
Пример 3. Определите значения коэффициентов экспоненциальной функции 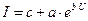 , аппроксимирующей ВАХ кремниевого диода (см. табл. 3) в диапазоне напряжений от 0 до 1В.
, аппроксимирующей ВАХ кремниевого диода (см. табл. 3) в диапазоне напряжений от 0 до 1В.
Возможность аппроксимации ВАХ диода экспоненциальным полиномом доказана в примере 2. Там же определена постоянная 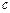 =-0,085.
=-0,085.
Составим уравнение прямой (см.рис.19):
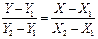 , (20)
, (20)
где 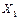 ,
, 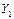 и
и 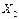 ,
, 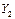 – координаты двух любых точек, через которые проходит данная прямая.
– координаты двух любых точек, через которые проходит данная прямая.
Выбираем 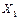 =0,
=0, 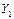 =-2,47 и
=-2,47 и 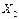 =1,
=1, 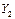 =-0,962 и получаем уравнение прямой:
=-0,962 и получаем уравнение прямой:
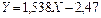 . (21)
. (21)
Сравнивая это выражение с прологарифмированным выражением (14):
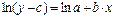 , (22)
, (22)
 получаем соотношения для определения неизвестных значений коэффициентов
получаем соотношения для определения неизвестных значений коэффициентов 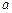 и
и 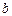 :
:
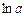 =-2,47,
=-2,47, 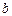 =1,538,
=1,538,
откуда 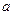 =0,085.
=0,085.
Таким образом аппроксимирующая функция:
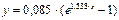 ,
,
или 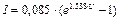 .
.
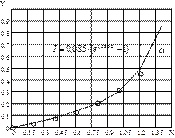
На рис.20 построена аппроксимирующая кривая и нанесены табличные знчения.
Рис.20. Аппроксимация ВАХ диода
На практике для аппроксимации характеристик в основном используют степенные полиномы:
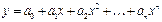 , (23)
, (23)
и кусочно-линейные функции.
Дата добавления: 2016-10-26; просмотров: 3278;











