Другие показатели наличия связи между признаками.

Корреляционное отношение.В классических статистических методах установления взаимосвязи между изучаемыми признаками в сельскохозяйственных и биологических исследованиях при наличии зависимости, имеющей криволинейный характер (в виде параболы, гиперболы, логарифмической функции, другого вида полиномы) не определяют коэффициент корреляции, поскольку он не даёт правильного представления о степени связи между признаками. В таких случаях было принято считать корреляционное соотношение η (эта), представляющая собой отношение двух дисперсий: дисперсии групповых средних и общей дисперсии.

При исследовании криволинейной зависимости можно вычислять два корреляционных отношения: η_у/х и η_х/у. В первом случае результативным признаком будет у, во втором – х. Однако реальный смысл имеет как правило один из двух показателей, притом результативный признак в классической статистике принято обозначать именно как у.

Корреляционное отношение вычисляют по формуле

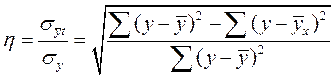,(53)

где 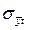– среднее квадратическое отклонение групповых средних;

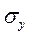– среднее квадратическое отклонение признака у;

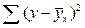– сумма квадратов отклонений вариант от частных средних

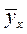, соответствующих определённым, фиксированным значениям независимой переменной х.

Аналогичной будет формула для определения η_х/у.

Корреляционное отношение всегда имеет положительный знак и принимает значения от нуля до единицы. Когда групповые средние 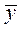не отличаются друг от друга, η = 0, то есть связь отсутствует. В случае прямолинейной связи коэффициент корреляции (его абсолютная величниа) и корреляционное отношение равны. Если связь криволинейная, то η > r.

Для определения степени приближения криволинейной зависимости к прямолинейной используется критерий криволинейности t:

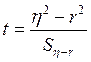; (54)

где 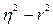- разность квадратов корреляционного отношения и коэффициента корреляции;

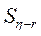- ошибка этой разности, которая определяется по формуле:

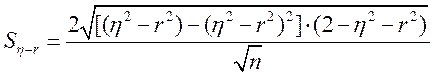. (55)

Отсюда:

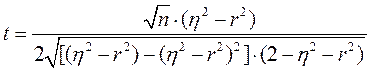. (56)

Вычисленную по формуле 49 или 51 величину t сравнивают с табличным её значением при избранном уровне значимости и числе степеней свободы df, равном n–2. Разность 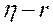считается существенной, если t_факт ≥ t_табл. В этом случае признают, что связь между признаками существенная криволинейная.

Коэффициент детерминации или аппроксимации (RI или R²).

Квадрат коэффициента корреляции (r²) называется коэффициентом детерминации или аппроксимации и обозначается RI или R².Этот коэффициент показывает долю (%) тех изменений, которые в данном явлении зависят от изучаемого фактора. Коэффициент детерминации является более непосредственным и прямым способом выражения зависимости одной величины от другой, и в этом отношении он предпочтительнее коэффициента корреляции. В случаях, где известно, что независимая переменная у находится в причинной связи с независимой переменной х, значение r² показывает ту долю элементов в вариации у, которая определена влиянием х. Так, например, если было установлено, что коэффициент корреляции между дозой азотного удобрений и содержанием белка в зерне составил 0,96, то можно утверждать, что 92% (0,96 · 0,96) колебаний содержания белка в зерне обусловлено варьированием доз азотного удобрения.

В практической статистике, коэффициенты детерминации или аппроксимации более широко используются при характеристике изучаемых взаимосвязей. Его можно использовать не только для описания прямолинейной связи между признаками, но и криволинейной (в этом случае, его называют коэффициент аппроксимации, и он представляет собой квадрат корреляционного отношения ).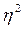

Обычно при определении взаимосвязи между изучаемыми признаками устанавливают последовательно коэффициент корреляции, коэффициент детерминации (или аппроксимации) и скорректированный коэффициент детерминации (RI_adj), который рассчитывается по формуле:

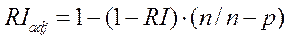. (57)

Именно, скорректированный коэффициент детерминации позволяет судить с высокой степенью вероятности о том, насколько процентов варьирование результативного признака обусловлено варьированием факториального.

Множественная корреляция.Корреляцияназывается множественной если на величину результативного признака одновременно влияют несколько факториальных.

Наиболее простой формой множественной связи является линейная зависимость между тремя признаками, когда один из них, например содержание белка в зерне , рассматривается как результативный признак функции у, а два другие – доза азотного удобрения и количество осадков за вегетацию – как аргументы x и z. В качестве меры тесноты линейной связи трёх признаков используют частные коэффициенты корреляции, обозначаемые r_xy·z, r_xz·y, r_zy·x, и множественные коэффициенты корреляции, обозначаемые символами R_xy·z, R_xz·y, R_zy·x.

Частные коэффициенты корреляции рассчитываются по формулам:

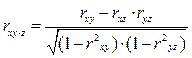; (58)

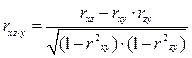; (59)

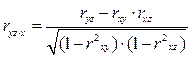. (60)

Ошибку и критерий значимости частной корреляции определяют аналогично, что и парной корреляции.

Множественный коэффициент корреляции нескольких переменных – это показатель тесноты связи между одним из признаков (буква индекса перед точкой) и совокупностью других признаков (буквы индекса после точки). Коэффициент корреляции трёх переменных рассчитывается по следующим формулам:

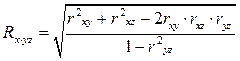; (61)

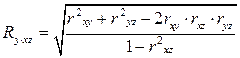; (62)

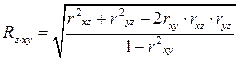. (63)

Эти формулы позволяют легко вычислить множественные коэффициенты корреляции при известных значениях коэффициентов парной корреляции. Коэффициент R положителен и всегда находится в пределах от 0 до 1.

Квадрат коэффициента множественной корреляции называется коэффициентом множественной детерминации, который, как и обыкновенный коэффициент детерминации, обозначается RI или R².

Значимость множественной корреляции оценивается по F – критерию:

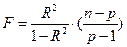, (64)

где n – объём выборки,

p – число независимых переменных или признаков.

Теоретическое значение F – критерия берут из приложения III для df₁ = р-1 и df₂ = n–p степеней свободы и принятого уровня значимости. Нулевая гипотеза о равенстве множественного коэффициента корреляции в совокупности нулю (Н₀ : R = 0) принимается, если F_факт < F_теор и отвергается, если F_факт ≥ F_теор.