Комбинационные схемы

Многие применения цифровой логики требуют наличия схем с несколькими входами и несколькими выходами, в которых выходные сигналы определяются текущими входными сигналами. Такая схема называется комбинационной схемой. Не все схемы обладают таким свойством. Например, схема, содержащая элементы памяти, может генерировать выходные сигналы, которые зависят от значений, хранящихся в памяти. Микросхема, которая реализует таблицу истинности (например, приведенную на рис. 3.3, а), является типичным примером комбинационной

схемы. В этом разделе мы рассмотрим наиболее часто используемые комбинационные схемы.

2.1.Мультиплексоры

На цифровом логическом уровне мультиплексор представляет собой схему с

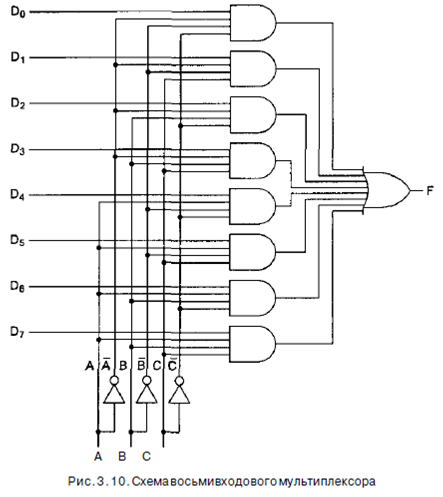
2" входами, одним выходом и п линиями управления, которые выбирают один из входов. Выбранный вход соединяется с выходом. На рис. 3.10 изображена схема восьмивходового мультиплексора. Три линии управления А, В и С кодируют 3-битное число, которое указывает, какая из восьми линий входа должна соединяться с вентилем ИЛИ и, следовательно, с выходом. Вне зависимости от того, какое значение будет на линиях управления, семь вентилей. И будут всегда выдавать на выходе 0, а оставшийся может выдавать или 0, или 1 в зависимости от значения выбранной линии входа. Каждый вентиль И запускается определенной комбинацией линий управления. Схема мультиплексора показана на рис. 3.10. Если к этому добавить источник питания и «землю», то мультиплексор можно запаковать в корпус с 14 выводами.

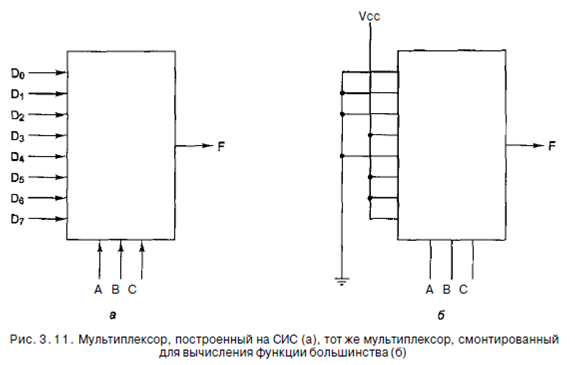
Используя мультиплексор, мы можем реализовать функцию большинства (см. рис. 3.3, а), как показано на рис. 3.11, б. Для каждой комбинации А, В и С выбирается одна из входных линий. Каждый вход соединяется или с Vcc (логическая 1), или с «землей» (логический 0). Алгоритм соединения входов очень прост: входной сигнал D; такой же, как значение в строке i в таблице истинности. На рис. 3.3, а в строках 0, 1, 2 и 4 значение функции равно 0, поэтому соответствующие входы заземляются; в оставшихся строках значение функции равно 1, поэтому соответствующие входы соединяются с логической 1. Таким способом можно реализовать любую таблицу истинности с тремя переменными, используя микросхему на рис. 3.11, а.

Мы уже видели, как мультиплексор может использоваться для выбора одного

из нескольких входов и как он может реализовать таблицу истинности. Его также можно использовать в качестве преобразователя параллельного кода в последовательный. Если подать 8 битов данных на линии входа, а затем переключать линии управления последовательно от 000 до i l l (это двоичные числа), 8 битов поступят на линию выхода последовательно. Обычно такое преобразование осуществляется при вводе информации с клавиатуры, поскольку каждое нажатие клавиши определяет 7- или 8-битное число, которое должно передаваться последовательно по телефонной линии.

Противоположностью мультиплексора является демультиплексор, который

соединяет единственный входной сигнал с одним из 2" выходов в зависимости от значений п линий управления. Если бинарное значение линий управления равно к, то выбирается выход к.

2.2.Декодеры

В качестве второго примера рассмотрим схему, которая получает на входе п-битное число и использует его для того, чтобы выбрать (то есть установить на значение 1) одну из 2" выходных линий. Такая схема называется декодером.

Пример декодера для п=3 показан на рис. 3.12.

Чтобы понять, зачем нужен декодер, представим себе память, состоящую из

8 микросхем, каждая из которых содержит 1 Мбайт. Микросхема 0 имеет адреса от 0 до 1 Мбайт, микросхема 1 - адреса от 1 Мбайт до 2 Мбайт и т. д. Три старших двоичных разряда адреса используются для выбора одной из восьми микросхем.

На рис. 3.12 эти три бита - три входа А, В и С В зависимости от входных сигналов ровно одна из восьми выходных линий (Do,..., D7) принимает значение 1; остальные линии принимают значение 0. Каждая выходная линия запускает одну из восьми микросхем памяти. Поскольку только одна линия принимает значение 1, запускается только одна микросхема.

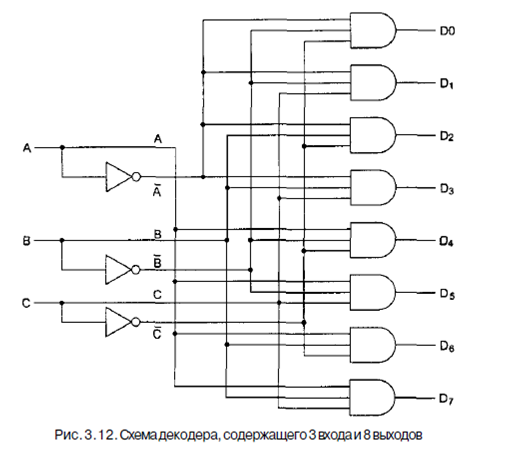
Принцип работы схемы, изображенной на рис. 3.12, не сложен. Каждый вен-

тиль И имеет три входа, из которых первый или А, или А, второй или В, или В, а третий или С, или С. Каждый вентиль запускается различной комбинацией входов: Do - сочетанием А В С, Di - А В С и т. д.

2.3.Компараторы

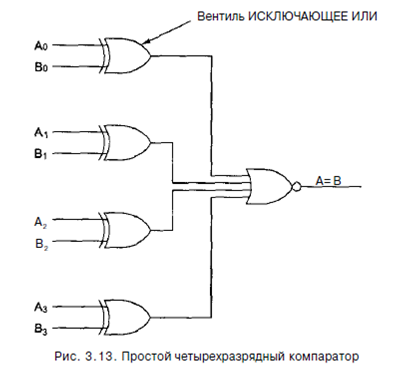
Еще одна полезная схема - компаратор. Компаратор сравнивает два слова, которые поступают на вход. Компаратор, изображенный на рис. 3.13, принимает два входных сигнала, А и В, каждый длиной 4 бита, и выдает 1, если они равны, и О, если они не равны. Схема основывается на вентиле ИСКЛЮЧАЮЩЕЕ ИЛИ, который выдает 0, если сигналы на входе равны, и 1, если сигналы на входе не равны. Если все четыре входных слова равны, все четыре вентиля ИСКЛЮЧАЮЩЕЕ ИЛИ должны выдавать 0. Эти четыре сигнала затем поступают в вентиль ИЛИ. Если в результате получается 0, значит, слова, поступившие на вход, равны; в противном случае они не равны. В нашем примере мы использовали вентиль ИЛИ в качестве конечной стадии, чтобы поменять значение полученного результата: 1 означает равенство, а 0 - неравенство.

2.4.Программируемые логические матрицы

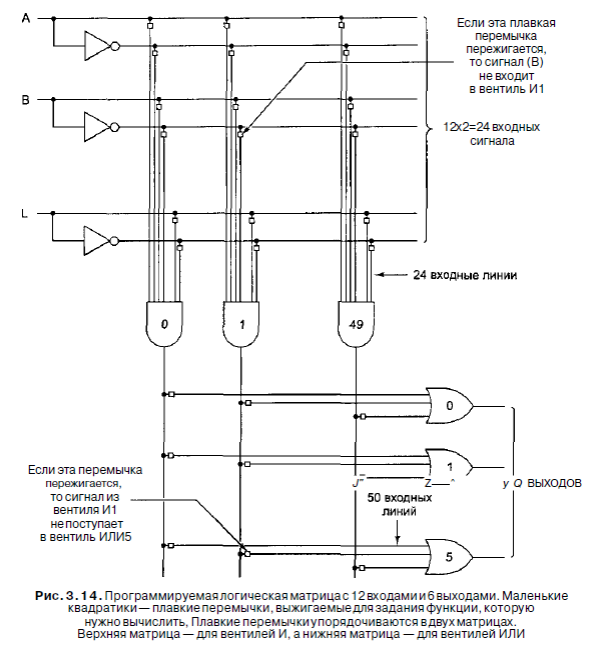
Ранее мы рассказывали, что любую функцию (таблицу истинности) можно представить в виде суммы произведений и, следовательно, воплотить в схеме, используя вентили И и ИЛИ. Для вычисления сумм произведений служит так называемая программируемая логическая матрица (рис. 3.14). Эта микросхема содержит входы для 12 переменных. Дополнительные сигналы (инверсии) генерируются внутри самой микросхемы. В итоге всего получается 24 входных сигнала. Какой именно входной сигнал поступает в определенный вентиль И, определяется по матрице 24x50 бит. Каждая из входных линий к 50 вентилям И содержит плавкую перемычку. При выпуске с завода все 1200 перемычек остаются нетронутыми. Чтобы запрограммировать матрицу, покупатель выжигает выбранные перемычки,

прикладывая к схеме высокое напряжение.

Выходная часть схемы состоит из шести вентилей ИЛИ, каждый из которых

содержит до 50 входов, что соответствует наличию 50 выходов у вентилей И. Какие из потенциально возможных связей действительно существуют, зависит от того, как была запрограммирована матрица 50x6. Микросхема имеет 12 входных выводов, 6 выходных выводов, питание и «землю» (то есть всего 20 выводов). Приведем пример использования программируемой логической матрицы. Рассмотрим схему, изображенную на рис. 3.3, б. Она содержит три входа, четыре вентиля И, один вентиль ИЛИ и три инвертора. Если запрограммировать нашу матрицу определенным образом, она сможет вычислять ту же функцию, используя три из 12 входов, четыре из 50 вентилей И и один из 6 вентилей ИЛИ. (Четыре вентиля И должны вычислять ABC, ABC, ABC И ABC; вентиль ИЛИ принимает эти 4 произведения в качестве входных данных.) Можно сделать так, чтобы та же программируемая логическая матрица вычисляла одновременно сумму четырех функций одинаковой сложности. Для простых функций ограничивающим фактором является число входных переменных, для более сложных - вентили И и ИЛИ.

Матрицы, программируемые в условиях эксплуатации, все еще используются. Однако предпочтение отдается матрицам, которые изготавливаются на заказ. Они разрабатываются заказчиком и выпускаются производителем в соответствии с запросами заказчика. Такие программируемые логические матрицы гораздо дешевле. А теперь мы можем обсудить три разных способа воплощения таблицы истинности, приведенной на рис. 3.3, а. Если в качестве компонентов использовать МИС, нам нужны 4 микросхемы. С другой стороны, мы можем обойтись одним мультиплексором, построенным на СИС, как показано на рис. 3.11, б. Наконец, мы можем использовать лишь четвертую часть программируемой логической матрицы. Очевидно, если необходимо вычислять много функций, использование программируемой логической матрицы более эффективно, чем применение двух других методов. Для простых схем предпочтительнее более дешевые МИС и СИС.