АЛГОРИТМ ПОСТРОЕНИЯ СТРУКТУРНОЙ СХЕМЫ
1. Вырачитт. член со старшей производной из дифференциального уравнения (1.3) и представить полученное соотношение с помощью сумматора, дифференцирующих и усилительных звеньев.
2. Все низшие производные получить как сигналы на соответствующих выходах последовательно соединенных интегрирующих звеньев.
3 Начальные условия (1.4) представить как постоянные во времени воздействия, приложенные на выходах интегрирующих звеньев.
Пример 1.1. Построить структурную схему системы, описываемой дифференциальным уравнением
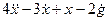
с начальными условиями 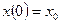 ,
, 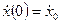 .
.
□ Выразим из уравнения член со старшей производной:
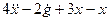 .
.
Изобразим схему получения сигнала 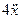 (рис. 1.9). С помощью усилительного члена с коэффициентом усиления 1/4 получим сигнал
(рис. 1.9). С помощью усилительного члена с коэффициентом усиления 1/4 получим сигнал 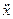 . Построим теперь прямую цепь схемы, последовательно преобразовывая сигнал
. Построим теперь прямую цепь схемы, последовательно преобразовывая сигнал 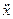 интегрирующими звеньями. Добавляя на выходах интегрирующих звеньев соответствующие начальные условия, получаем часть прямой цепи схемы, в которой присутствуют выходной сигнал
интегрирующими звеньями. Добавляя на выходах интегрирующих звеньев соответствующие начальные условия, получаем часть прямой цепи схемы, в которой присутствуют выходной сигнал 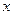 и его производные
и его производные 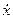 ,
, 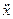 . Изображаем сумматор, выходным сигналом коюрого служит
. Изображаем сумматор, выходным сигналом коюрого служит 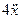 . На этом сумматоре нужно реализовать равенство
. На этом сумматоре нужно реализовать равенство
 .
.
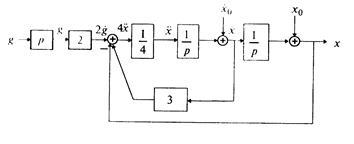
Рис. 1.9
Для этого добавляем к прямой цепи соединение дифференцирующего и усилительного звеньев, которые из входного сигнала g позволяют получить нужный сигнал 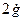 на входе сумматора. Сигналы
на входе сумматора. Сигналы 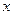 и
и 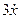 подаем на сумматор с соответствующим знаком, используя обратные связи. Таким образом, получаем структурную схему (рис. 1.9), соответствующую заданному дифференциальному уравнению.
подаем на сумматор с соответствующим знаком, используя обратные связи. Таким образом, получаем структурную схему (рис. 1.9), соответствующую заданному дифференциальному уравнению.
Пример 1.2. Построить структурную схему системы, описываемой дифференциальным уравнением
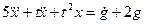
с начальными условиями 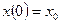 ,
, 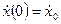 ,
, 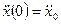 .
.
□ Выразим из уравнения член со старшей производной:
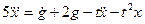 .
.
Согласно алгоритму получим структурную схему системы (рис. 1.10).
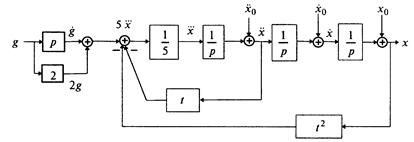
Рис. 1.10
Пример 1.3. Построить структурную схему системы, описываемой дифференциальным уравнением
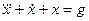 .
.
□ Выразим из уравнения член со старшей производной:
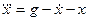
и с помощью алгоритма получим схему (рис. 1.11).
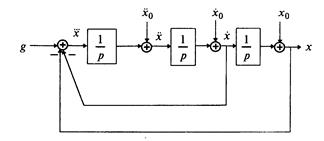
Рис. 1.11
2. Составление дифференциального уравнения по структурной схеме. Для записи дифференциального уравнения следует обозначить на схеме все промежуточные сигналы, записать уравнения для каждого звена и для каждого сумматора и из полученной системы дифференциальных и алгебраических уравнений исключить промежуточные переменные кроме входного и выходного сигналов.
Пример 1.4. Составить дифференциальное уравнение по структурной схеме, изображенной на рис. 1 12.
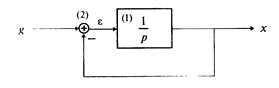
Рис. 1.12
□ Составим уравнения элементов схемы:
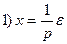 ;
; 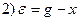 .
.
Отсюда
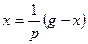 ,
, 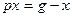 ,
, 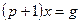 .
.
Дифференциальное уравнение системы имеет вид
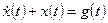 ,
,
что совпадает с (1.10) при 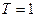 , т.е. система, состоящая из интегрирующего звена, замкнутого отрицательной обратной связью, является апериодическим звеном.
, т.е. система, состоящая из интегрирующего звена, замкнутого отрицательной обратной связью, является апериодическим звеном.
Пример 1.5. Составить дифференциальное уравнение по структурной схеме, представленной на рис. 1.13.
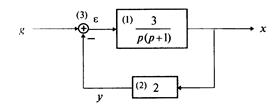
Рис. 1.13
□ Составим уравнения элементов схемы:
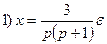 ;
; 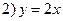 ;
; 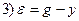 .
.
Отсюда
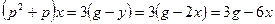 .
.
Переходя от операторной формы записи дифференциального уравнения к обычной, получаем
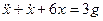 .
.
Дата добавления: 2017-09-01; просмотров: 9164;











