Решение уравнения (1) имеет вид

x = x_m соs (w_ot + a) , (2)

где x_m – амплитуда колебания, наибольшее значение величины, совершающей колебания;

(w₀t + a) – фаза колебания;

a – начальная фаза, т.е. фаза в момент t = 0;

w₀ – собственная круговая частота колебания (число колебаний за 2p секунд).

Используются также следующие понятия:

T – период колебания (время одного полного колебания). T = 2p/w₀.

n – частота колебания (число колебаний за 1 секунду): .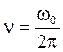

Для рассматриваемых осцилляторов периоды колебаний равны:

пружинного маятника 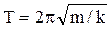; (3)

для математического 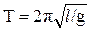; (4)

для физического 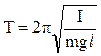. (5)

В формуле (5) величина I – момент инерции физического маятника относительно оси O.

Энергия гармонического осциллятора складывается из кинетической и потенциальной энергий и в любой момент времени остается постоянной:

E = kx_m²/2 или E = mw₀²x_m²/2 . (6)

2. Свободные затухающие колебания

При малых колебаниях и небольших скоростях сила сопротивления среды пропорциональна величине скорости F_сопр = – rV, где r – постоянная, называемая коэффициентом сопротивления. Тогда уравнение колебаний можно представить следующим образом:

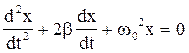, (7)

где ; w₀ – собственная частота колебаний.

Решение уравнения (7) ( при условии w₀>b ) имеет вид

x = x_m0e^-btcos(wt+a), (8)

где 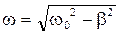. (9)

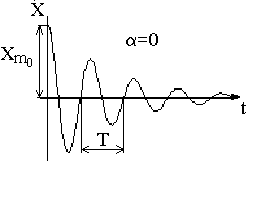
График этой функции дан на рис. 2.

Рис. 2

Таким образом, данные колебания можно рассматривать как гармонические с частотой w и с амплитудой, убывающей по закону

x_m(t) = x_m0e^-bt (10)

Для характеристики быстроты затухания колебаний применяется несколько величин:

b – коэффициент затухания, величина обратная времени, за которое амплитуда колебаний уменьшится в e раз;

t – время релаксации, за которое амплитуда колебаний уменьшится в e раз: ;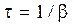

l - логарифмический декремент затухания. По определению – это натуральный логарифм двух последовательных амплитуд колебаний.

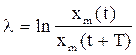. (11)

По физическому смыслу l – это величина, обратная числу колебаний, за время которых амплитуда колебаний уменьшится в e раз. Связь его с коэффициентом затухания выражается формулой

l = bT ; (12)

Q – добротность колебательной системы. По определению Q – это отношение числа p к логарифмическому декременту затухания колебаний:

Q = p/l . (13)

Если в уравнении (7) b³w₀, то колебания в системе невозможны. При выведении ее из положения равновесия происходит апериодический процесс возврата системы в исходное состояние.

3. Вынужденные колебания

Если вынуждающая сила, действующая на колебательную систему, изменяется по гармоническому закону

F = F_m cos(Wt) ,

то дифференциальное уравнение вынужденных колебаний можно представить в виде

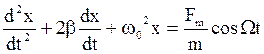, (14)

где b – коэффициент затухания , а w₀ – собственная частота колебаний системы. Это неоднородное дифференциальное уравнение (с правой частью, не равной нулю). Из теории дифференциальных уравнений известно, что общее решение уравнения такого вида представляет собой сумму общего решения однородного уравнения затухающих колебаний, рассмотренного ранее, и частного решения данного неоднородного уравнения. При этом первое убывающее слагаемое играет роль только во время установления колебаний. На рис. 3 показан примерный вид зависимости x(t), описываемой уравнением (14).

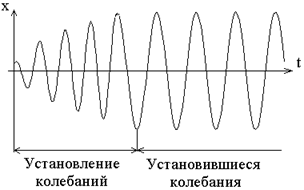
B установившемся режиме вынужденные колебания являются гармоническими, незатухающими, происходят с частотой вынуждающей силы W. Их уравнение

x = x_mcos (Wt + j) (15)

Рис. 3

При этом амплитуда x_m вынужденных колебаний равна 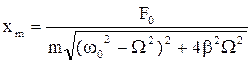, (16) а сдвиг фаз этих колебаний j по отношению к вынуждающей силе определяется из равенства

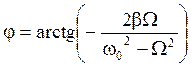. (17)

Зависимость вынужденных колебаний от частоты вынуждающей силы (16) приводит к тому, что при некоторой определенной для данной системы частоте амплитуда колебаний достигает максимального значения. Это явление называется резонансом, а соответствующая частота – резонансной частотой. Исследование равенства (16) дает

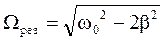. (18)

Рис. 4

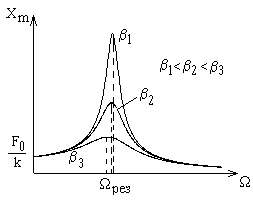
Графики зависимости амплитуды вынужденных колебаний от частоты вынуждающей силы W (резонансные кривые), соответствующие различным значениям параметра b, показаны на рис. 4.

4. Сложение гармонических колебаний

При сложении двух гармонических колебаний, одинаково направленных и одинаковой частоты, описываемых уравнениями

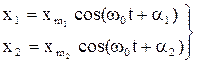, (19)

результирующее колебание будет также гармоническим и иметь частоту w₀:

x = x_mcos(w₀t + a) , (20)

где амплитуда x_m и начальная фаза a равны соответственно:

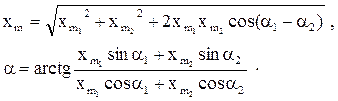(21)

При сложении двух гармонических колебаний одного направления с мало отличающимися частотами, которые задаются уравнениями

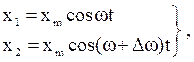(22)

где Dw << w, результирующее колебание является гармоническим с пульсирующей амплитудой. Такие колебания называются биениями.

Уравнение биений имеет вид

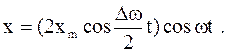(23)

При сложении двух взаимно перпендикулярных колебаний одинаковой частоты, уравнения которых имеют вид

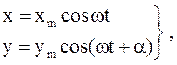(24)

точка движется по траектории

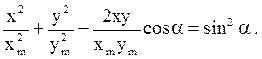(25)

В зависимости от разности фаз a складываемых колебаний возможны частные случаи:

1. a = 0 – точка движется по прямой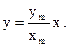

2. a = ±p – точка движется по прямой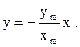

В обоих случаях это гармоническое колебание, происходящее по закону

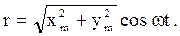(26)

3. a = ±p/2 – точка движется по эллипсу, уравнение которого:

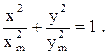(27)