Основы теории зубчатого зацепления.

От зубчатой передачи (см.рис. 7.2, а) требуется, чтобы передаточное отношение u₁₂ оставалось строго постоянным. На первый взгляд может показаться, что это будет само собой выполняться, если расположить зубья равномерно по окружностям r_{w1 и} r _w2. Однако этого не достаточно для обеспечения u₁₂=const. Рассмотрим графики на рис. 7.2, на которых по оси ординат отложены значения передаточного отношения в функции угла поворота ведущего колеса. График на рис. 7.2, а представляет волнистую линию. Даже небольшие изменения передаточного отношения на больших скоростях делаются весьма ощутительными: приводят к неспокойному ходу, сопровождаются ударами в зубьях. Таким образом, проблема обеспечения u₁₂=const наряду с условием расположения зубьев по окружности связывается с необходимостью соответственного профилирования зубьев.

а)неправильное зацепление б) правильное зацепление

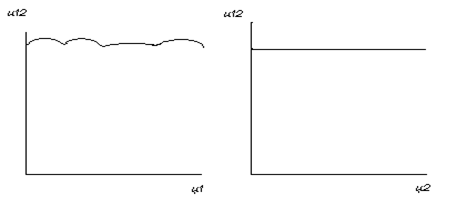
Рис 7.2Возможные схемы реализации передаточного отношения пары зубчатых колес

а)без учета соответствия боковых профилей зубьев друг другу;

б)с учетомспециального выбора сопряженных профилей зубьев

Основная теорема зацепления.Синтез зацепления следует производить в направлении отыскания сопряженных поверхностей по заданному закону их относительного движения. Основная теорема зацепления устанавливает связь между геометрией сопряженных поверхностей и законом относительного движения элементов высшей кинематической пары.

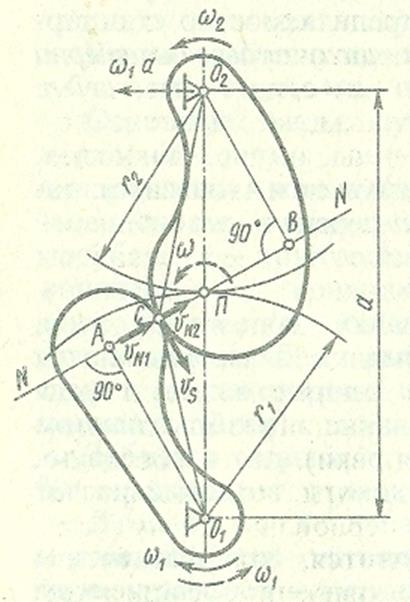
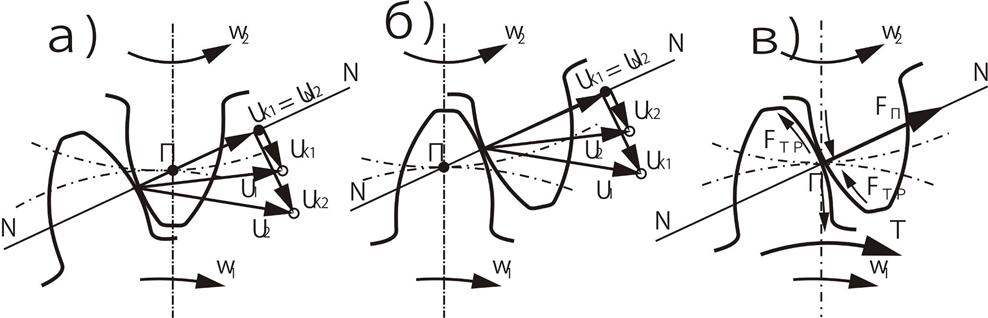
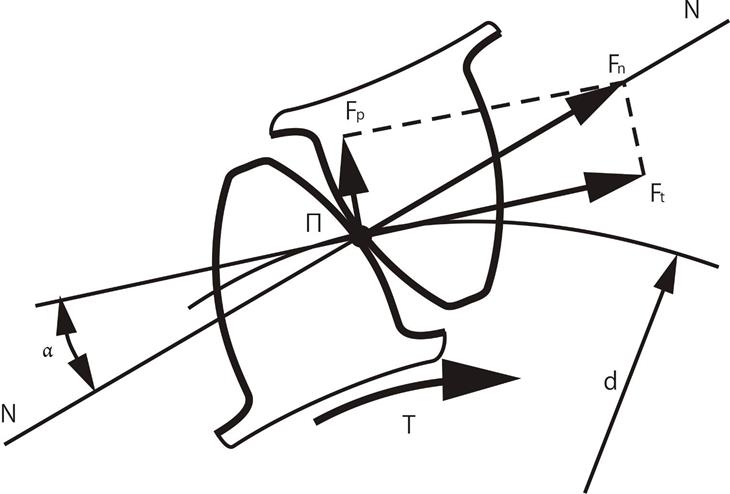
Для доказательства теоремы о мгновенном передаточном отношении рассмотрим пару сопряженных зубьев в плоском зацеплении (см. рис 7.3).

На это место поместить цветную копию !!!

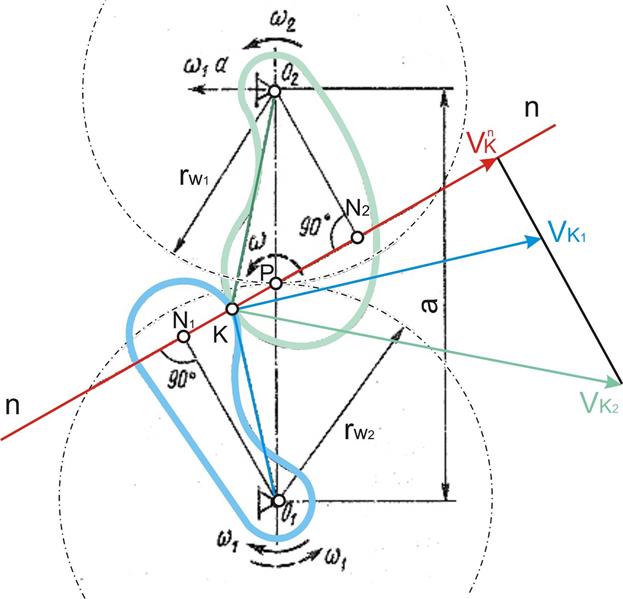
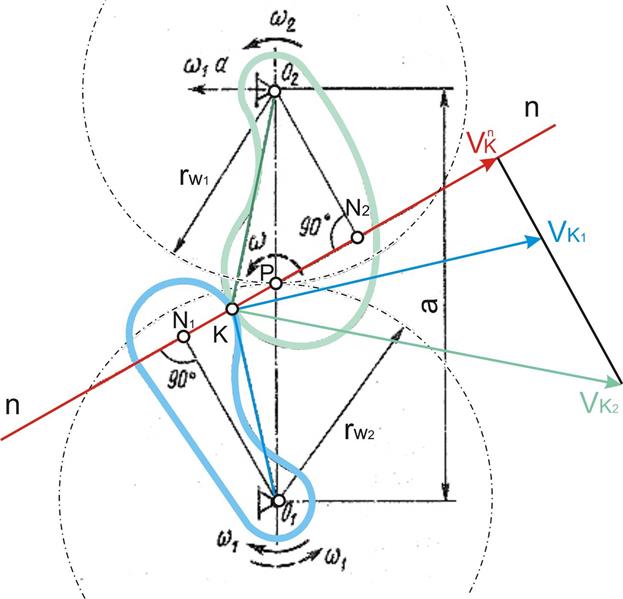
Профили зубьев шестерни и колеса касаются в точке К, называемой точкой зацепления. Центры вращения О₁ и О₂ расположены на расстоянии а_w друг от друга. Боковой профиль зуба шестерни, которая вращается с угловой скоростью ω₁, действует на зуб колеса, сообщая последнему угловую скорость ω₂. Проведем через точку К общую для обоих профилей нормаль n-n и касательную t-t. Окружные скорости точек К₁ и К₂ относительно центров вращения О₁ и О₂

υ_к1=ω₁·О₁К и υ_к2=ω₂·О₂К

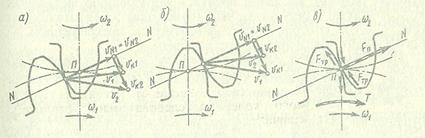
Разложим υ_к1 и υ_к2 на составляющие υ_к1ⁿ и υ_к2ⁿ по направлению нормали n-n и составляющие υ_к1^τ и υ_к2^τ по направлению к касательной. Условие контакта (сопряжения) звеньев будет обеспечено лишь при равенстве нормальных составляющих скоростей

Пр _n-n υ_к1= υ_к1ⁿ= υ_к2ⁿ= Пр _n-n υ_к2

В противном случае при υ_к1ⁿ > υ_к2ⁿ произойдет врезание зубьев, а при υ_к1ⁿ < υ_к2ⁿ зуб шестерни отстанет от зуба колеса.

Из подобия треугольников О₁АР и О₂ВР найдем:

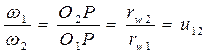
Последнее выражение известно в научно-технической литературе, как математическая трактовка теоремы Виллиса, которая обуславливает кинематику передачи движения двумя звеньями с неподвижными параллельными осями, образующими высшую кинематическую пару. Теорема формулируется так: общая нормаль n-n к профилям высшей кинематической пары, построенная в точке их контакта делит межцентровое расстояние О₁О₂ на части О₁Р и О₂Р, обратно пропорциональные угловым скоростям ω₁ и ω₂.

Следствие из теоремы. Поскольку для круглых зубчатых колес требуется u₁₂=const, то общая нормаль должна пересекать межцентровое расстояние всегда в одной точке Р, то есть выполняется условие О₁Р=const и О₂Р=const.

Таким образом точка Р оказывается неподвижной в пространстве и называется полюсом.

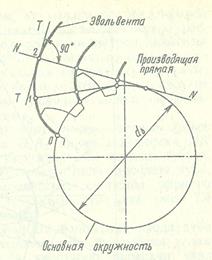
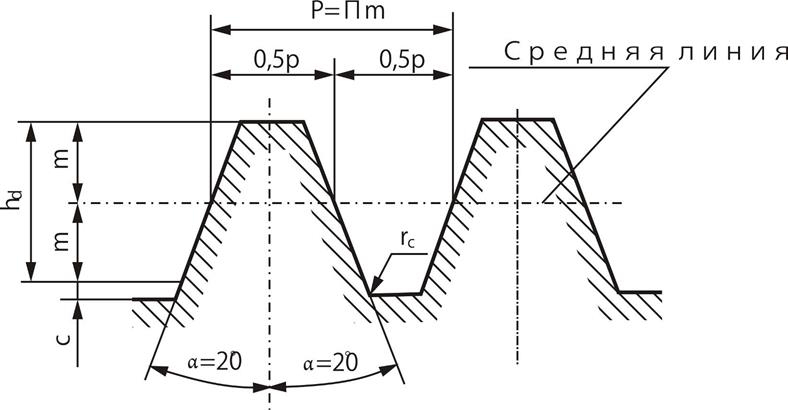
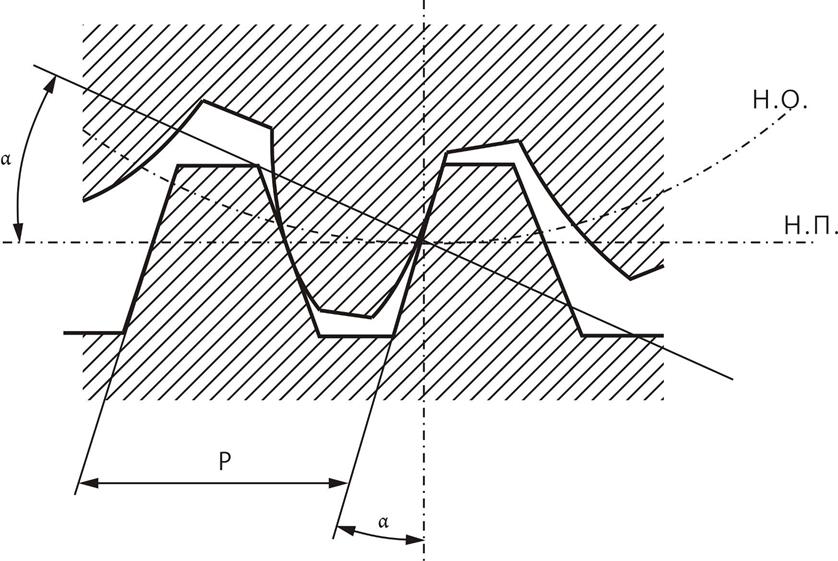
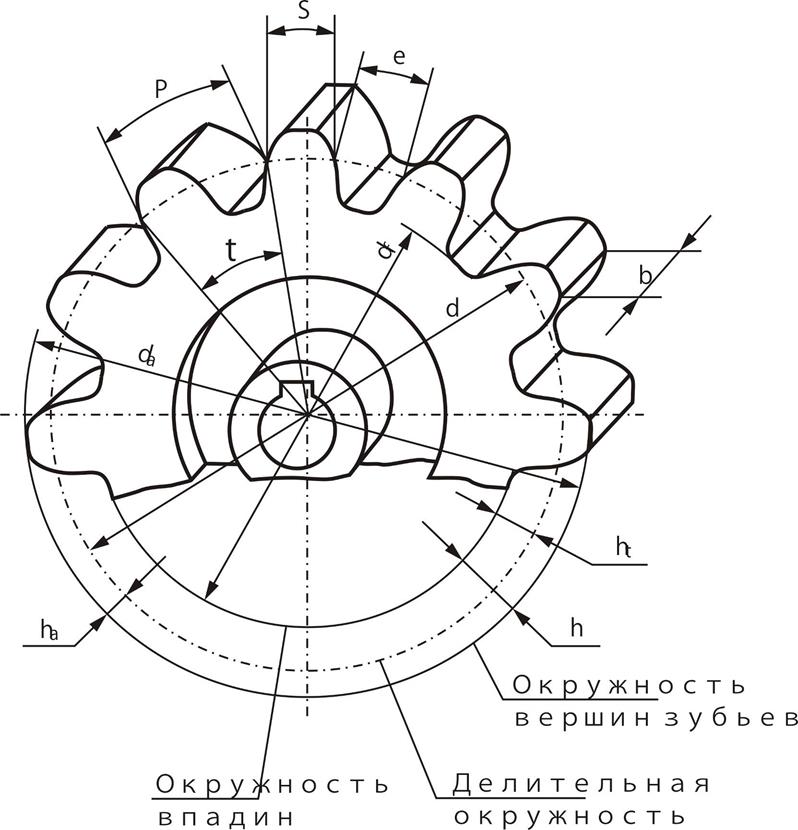
Для передач следует использовать профили наиболее технологичные при изготовлении и эксплуатации. В частности ими могут быть профили эвольвентный, циклоидальный и др. Наиболее распространенной в машиностроении является зубчатая передача с линией зацепления в виде прямой линии, следовательно с постоянным углом зацепления α. Такое зацепление было предложено Л.Эйлером (в 1765г. ?). И носит название эвольвентного, поскольку соответствующие профили зубьев получаются по эвольвентным кривым. Особое распространение эвольвентных передач объясняется значительными преимуществами их перед известными и опробованными в настоящее время передачами. Так, эвольвентные передачи в определенных пределах допускают изменение межосевого расстояния, сохраняя постоянство передаточного отношения в процессе зацепления, и обладают хорошими эксплуатационными качествами. Инструмент для нарезания колес простой, несложен и процесс изготовления колес.