ОО: упорядоченные двойки (пары) людей
| А2 |
| В2 |
| С2 |
| А12 |
| В12 |
| А22 |
| С12 |
А2(x,у) В2(x,у) – внеположенность(1) ;
А2(x,у) С2(x,у) – внеположенность (2) ;
А2(x,у) А12(x,у)– внеположенность (3) ;
А2(x,у) В12(x,у) – внеположенность (4) ;
А2(x,у) С12(x,у) – внеположенность (5) ;
А2(x,у) А22(x,у) – внеположенность (6) ;
В2(x,у) С2(x,у) – внеположенность (7) ;
В2(x,у) А12(x,у) – внеположенность (8) ;
В2(x,у) В12(x,у) – внеположенность (9) ;
В2(x,у) С12(x,у) – внеположенность (10) ;
В2(x,у) А22(x,у) – внеположенность (11) ;
С2(x,у) А12(x,у) – внеположенность (12) ;
С2(x,у) С12(x,у) – внеположенность (13) ;
С2(x,у) А22(x,у) – внеположенность (14) ;
С2(x,у) В12(x,у) – внеположенность (15) ;
А12(x,у) В12(x,у) – внеположенность (16) ;
А12(x,у) С12(x,у) – внеположенность (17) ;
А12(x,у) А22(x,у) – внеположенность (18) ;
В12(x,у) С12(x,у) – перекрещивание (19) ;
В12(x,у) А22(x,у) – перекрещивание (20) ;
С12(x,у) А22(x,у) – перекрещивание (21) .
Разъяснения.В случаях (1), (3), (7), (12) перекрещивание понятий исключается принципом причинности, регулирующим родственные отношения, зафиксированные в используемых здесь понятиях. Принцип причинности (ПП) применительно к данным случаям сводится к двум утверждениям:
(ПП1) каждый человек связан со своей матерью причинно-следственной связью (а через мать и отца – с бабушкой и дедушкой);
(ПП2) причина предшествует действию во времени.
В случае (1), например:
(1.1) если а есть мать b, то неверно, что b есть мать а, то есть если áа, bñÎ{áх, уñ½х – мать у}, то áb, аñÏ{áх, уñ½х – мать у};
(1.2) если а есть дочь b, то неверно, что b есть дочь а, то есть: если áа, bñÎ{áх, уñ½х – дочь у}, то áb, аñÏ{áх, уñ½х – дочь у},
где áа, bñÏ{áх, уñ½R2(x, у)} означает Øáа, bñÎ{áх, уñ½R2(x, у)}.
Симметричным в логике называют ненулевое бинарное (двуместное) отношение R2(x, у), для которого справедливо условие:
если áа, bñÎ{áх, уñ½R2(x, у)}, то áb, аñÎ{áх, уñ½R2(x, у)} (в предположении, что существует хотя бы одна пара áа, bñ такая, что áа, bñÎ{áх, уñ½R2(x, у)}, то есть понятие R2(x, у)не является нулевым).
Ненулевое бинарное отношение R2(x, у), для которого выполняется условие
если áа, bñÎ{áх, уñ½R2(x, у)}, то áb, аñÏ{áх, уñ½R2(x, у)}, называют асимметричным.
Отношения А2(x, у): x – мать у и В2(x, у): x – дочь у являются асимметричными; кроме того, если áа, bñÎ{áх, уñ½х – мать у} и bÎ{х½х – дочь}, то áb, аñÎ{áх, уñ½х – дочь у}; а поэтому объемы этих понятий не пересекаются: А2ÇВ2=Æ,
где: А2 D {áх, уñ½А2(x, у)}; В2 D {áх, уñ½В2(x, у)};Æ – пустое множество,
то есть: (1) А2(x, у) В2(x, у) – внеположенность.
Аналогично асимметричными являются отношения:
С2(x, у): х – бабушка у и 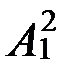 (x, у): х – внучка у; С2ÇА12=Æ;
(x, у): х – внучка у; С2ÇА12=Æ;
то есть: (12) С2(x, у) 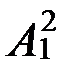 (x, у) – внеположенность.
(x, у) – внеположенность.
Отношение С2(x, у) : х – бабушка у выражается через отношения х – мать у и, возможно, х – отец у, также подчиненные принципу причинности:
х – бабушка у =Df $z- человек (х – мать zÙ(z – мать уÚ z – отец у));
С2(x, у) =Df $z- человек (A2(x, z)Ù( A2(z, у)Ú B2(z, у))),
где В2(x, у): х – отец у; знак =Df является знаком реального определения, читается «…равно по определению…».
Аналогично отношение 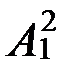 (x, у): х – внучка у выражается через отношения х – дочь у и, возможно, х – сын у, также подчиненные принципу причинности:
(x, у): х – внучка у выражается через отношения х – дочь у и, возможно, х – сын у, также подчиненные принципу причинности:
х – внучка у =Df $z- человек (х – дочь zÙ(z – дочь уÚ z – сын у));
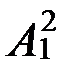 (x, у) =Df $z- человек (В2(x, z)Ù(В2(z, у)Ú С22(z, у))),
(x, у) =Df $z- человек (В2(x, z)Ù(В2(z, у)Ú С22(z, у))),
где  (x, у): х – сын у.
(x, у): х – сын у.
Отсюда: (3) А2(x,у) 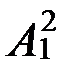 (x,у) - внеположенность, т. е. А2Ç
(x,у) - внеположенность, т. е. А2Ç 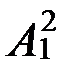 =Æ;
=Æ;
(7) В2(x,у) С2(x,у) – внеположенность, т. е. В2ÇС2=Æ.
Отношения кровного родства можно представить с помощью направленного графа без петель.
Графом* называют совокупность точек на плоскости (вершин графа), соединенных друг с другом линиями (дугами графа). Если каждой дуге сопоставлено направление (от начальной вершины до конечной), граф называется направленным. Петлей называют дугу, начальная и конечная вершины которой совпадают, то есть дугу вида ám,mñ:
m – вершина графа.
m
Симметричное отношение представляется направленным графом, каждая пара вершин которого соединяется двумя противоположно направленными дугами: (mi, mj – i-тая и j-тая вершины графа; i=1, 2, …, n; j=1, 2, …, n; i¹j):
mi mj .
Асимметричное отношение представляется направленным графом, в котором отсутствуют пары вершин, соединенные противоположно направленными дугами; то есть все вершины в таком графе соединены лишь одинарными дугами:
mi mj .
Рефлексивное отношение, то есть ненулевое отношение R2(x, у), удовлетворяющее условию: для каждого аÎU: aR2a истинно, (U – универсум рассуждения), изображается направленным графом, каждая вершина которого снабжена петлей:
mi .
Транзитивное отношение, то есть ненулевое отношение R2(x, у), удовлетворяющее условию: для каждых аÎU, bÎU, сÎ U: если aR2b и bR2с, то aR2с, изображается направленным графом, в котором все вершины разбиты на тройки, соединенные следующим образом:
mj mk
mi .
Для родственных отношений U – множество людей; кровная связь между родителями и детьми изображается дугами. Направление дуг определяется принципом причинности и совпадает с направлением времени:
а b
(мать) (отец)
с
(сын или дочь) .
Направленный граф, представляющий родственное отношение, не может содержать петли; каждая пара вершин его соединена не более чем одной дугой (асимметричность отношения родители-дети); в каждую вершину приходят две и только две дуги (каждый человек имеет двух и только двух родителей); число дуг, исходящих из каждой вершины, ограничено (в общем не более ста).
Родственные отношения, представленные в задаче, не являются транзитивными.
В случаях (1), (3), (7), (12) родственные отношения представляются направленными графами:
(1) А2(x,у) В2(x,у) а с
áа, bñÎ{áх, уñ½х – мать у}
áb, аñÎ{áх, уñ½х – дочь у}
b
(перекрещивание невозможно в силу асимметричности А2(x,у) и В2(x,у)).
(12) С2(x,у) 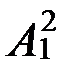 (x,у) а а1
(x,у) а а1
áа, bñÎ{áх, уñ½х – бабушка у}
áb, аñÎ{áх, уñ½х – внучка у} с b1
b
(перекрещивание невозможно в силу асимметричности С2(x,у) и 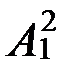 (x,у)).
(x,у)).
(3) A2(x,у) 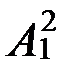 (x,у)
(x,у)
áа, сñÎ{áх, уñ½х – мать у}
áb, аñÎ{áх, уñ½х – внучка у}
(перекрещивание невозможно в силу нетранзитивности А2(x,у) и 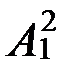 (x,у)).
(x,у)).
(7) В2(x,у) С2(x,у)
áс, аñÎ{áх, уñ½х – дочь у}
áа, bñÎ{áх, уñ½х – бабушка у}
(перекрещивание невозможно в силу нетранзитивности В2(x,у) и С2(x,у)).
В случаях (15) и (17) перекрещивание понятий невозможно по законам биологии (даже при допущении кровосмешения):
(15) С2(x,у) 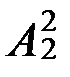 (x,у) (17)
(x,у) (17) 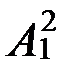 (x,у)
(x,у)  (x,у)
(x,у)
áа, bñÎ{áх, уñ½х – бабушка у} áс, аñÎ{áх, уñ½х – внучка у}
áа, bñÎ{áх, уñ½х – племянница у} áс, аñÎ{áх, уñ½х – тетя у}
а1
b1
а
b с
а1 рождает b от своего правнука с или с рождает b от своего прадеда а1, что практически невозможно (по законам биологии).
В случаях (2), (4), (5), (6), (8), (9), (10), (11), (13), (14), (16), (18) перекрещивание понятий принципом причинности и законами биологии не запрещается, но возможно лишь при допущении кровосмешения.
(2) А2(x,у) С2(x,у) (8) В2(x,у) 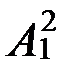 (x,у)
(x,у)
áа, bñÎ{áх, уñ½х – мать у} áb, аñÎ{áх, уñ½х – дочь у}
áа, bñÎ{áх, уñ½х – бабушка у} áb, аñÎ{áх, уñ½х – внучка у}
| а рождает дочь b от своего сына с. |
с
b
(4) А2(x,у) 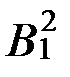 (x,у) (9) В2(x,у)
(x,у) (9) В2(x,у) 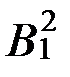 (x,у)
(x,у)
áа, bñÎ{áх, уñ½х – мать у} áb, аñÎ{<х, уñ½х – дочь у}
áа, bñÎ{áх, уñ½х – сестра у} áb, аñÎ{<х, уñ½х – сестра у}
а с
b
а рождает дочь b от своего отца с.
(5) А2(x,у) 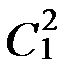 (x,у) (11) В2(x,у)
(x,у) (11) В2(x,у) 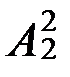 (x,у)
(x,у)
áа, bñÎ{áх, уñ½х – мать у} áb, аñÎ{áх, уñ½х – дочь у}
áа, bñÎ{áх, уñ½х – тетя у} áb, аñÎ{áх, уñ½х – племянница у}
а1
а с
b а рождает дочь b от своего брата с.
(6) А2(x,у) 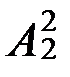 (x,у) (10) В2(x,у)
(x,у) (10) В2(x,у) 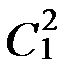 (x,у)
(x,у)
áа, bñÎ{áх, уñ½х – мать у} áb, аñÎ{áх, уñ½х – дочь у}
áа, bñÎ{áх, уñ½х – племянница у} áb, аñÎ{áх, уñ½х – тетя у}
а1
c
a
b
а рождает дочь b от своего деда а1.
(13) С2(x,у) 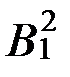 (x,у) (16)
(x,у) (16) 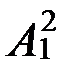 (x,у)
(x,у) 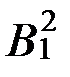 (x,у)
(x,у)
áа, bñÎ{áх, уñ½х – бабушка у} áb, аñÎ{áх, уñ½х – дочь у}
áа, bñÎ{áх, уñ½х – сестра у} áb, аñÎ{áх, уñ½х – сестра у}
а1
а с
b
с– дочь, рожденная а от ее отца а1; b – дочь, рожденная с от а1.
(14) С2(x,у) 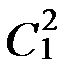 (x,у) (18)
(x,у) (18) 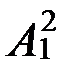 (x,у)
(x,у) 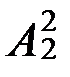 (x,у)
(x,у)
áа, bñÎ{áх, уñ½х – бабушка у} áb, аñÎ{áх, уñ½х – внучка у}
áа, bñÎ{áх, уñ½х – тетя у} áb, аñÎ{áх, уñ½х – племянница у}
а1
а
b1
с
b
с рождает дочь b от своего дяди b1.
В случаях (19), (20), (21) имеет место перекрещивание понятий:
(19) 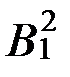 (x,у)
(x,у) 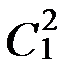 (x,у) (20)
(x,у) (20) 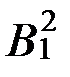 (x,у)
(x,у) 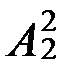 (x,у)
(x,у)
áа, bñÎ{áх, уñ½х – сестра у} áb, аñÎ{áх, уñ½х – сестра у}
áа, bñÎ{áх, уñ½х – тетя у} áb, аñÎ{áх, уñ½х – племянница у}
а1 b
· с
а b1
b1 рождает дочь а от а1, а затем дочь b1 от другого брака с рождает дочь b от а1 (кровосмешения нет).
(21) 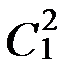 (x,у)
(x,у) 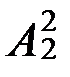 (x,у)
(x,у)
áа, bñÎ{áх, уñ½х – тетя у} áb, аñÎ{áх, уñ½х – тетя у}
áа, bñÎ{áх, уñ½х–племянница у} áb, аñÎ{áх, уñ½х–племянница у}
а1 b1 b
·
·
a c1 c
с1 (дочь с) рождает дочь а от а1, а с рождает дочь b от b1 (сына а1) или а1 рождает дочь а от с1 (сына с), а b1 рождает дочь b от с.
Множество 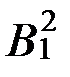 Ç
Ç 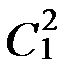 Ç
Ç 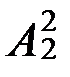 =Æ, так как одновременное выполнение условий:
=Æ, так как одновременное выполнение условий:
áа, bñÎ{áх, уñ½х – сестра у}
áа, bñÎ{áх, уñ½х – тетя у}
áа, bñÎ{áх, уñ½х–племянница у}
невозможно; выполнение этих условий означало бы наличие в предшествующем направленном графе прямых дуг от а1 к b или от с к а:
а1 b1 b
·
·
a c1 c
что означало бы, что в вершину b (или с) приходит три дуги, а это невозможно (по законам биологии).
Таким образом, на рис. 3.2 изображено отношение понятий родственных отношений в предположении запрета на кровосмешение.
Дата добавления: 2021-01-26; просмотров: 536;











