СЛУЧАЙНЫЕ ПОГРЕШНОСТИ

Теория погрешностей, использующая математический аппарат теории вероятностей, основывается на аналогии между появлением случайных погрешностей при многократно повторенных измерениях и появлением случайных событий. Из теории вероятностей известно, что для характеристики случайных величин, в нашем случае погрешностей прибора или измерения (вместе с их систематической составляющей), необходимо определить их закон распределения.

В теории случайных погрешностей формулируются две аксиомы. Аксиома симметрии (случайности) - при очень большом числе измерений случайные погрешности, равные по величине, но различные по знаку, встречаются одинаково часто. Аксиома распределения - чаще всего встречаются меньшие погрешности, а большие погрешности встречаются тем реже, чем они больше.

Если эти аксиомы соблюдаются, то при неограниченном увеличении числа независимых причин, вызывающих погрешности, мы имеем нормальный закон распределения случайной погрешности.

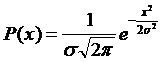(2.3)

где P(х) - плотность вероятности случайной величины X; s - среднее квадратическое отклонение.

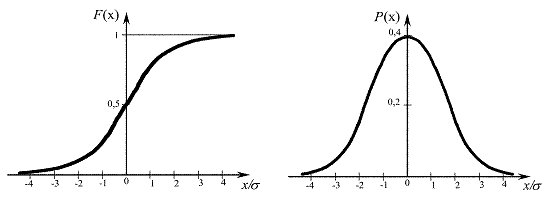
Рис. 2.1. Интегральный и дифференциальный законы распределения

Одно из нарушений нормального закона распределения погрешностей при соблюдении аксиом состоит в появлении плосковершинности и островершинности, как показано на рис. 2.2.

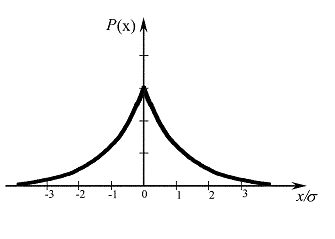
Рис. 2.2. Островершинное распределение

В пределе для плосковершинного распределения, когда уже аксиома не соблюдается, оно превращается в равномерное.

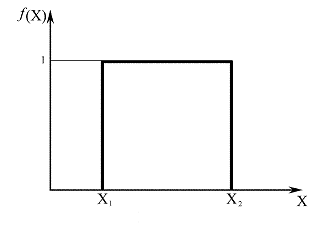
Рис. 2.3. Равномерное (равновероятное) распределение

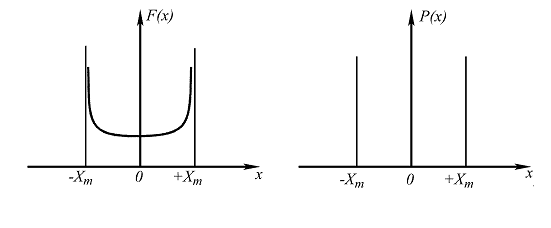
Рис. 2.4. Двухмодальное распределение

Модой дискретной случайной величины называют ее наиболее вероятное значение, а для непрерывной случайной величины модой является то значение, при котором плотность вероятности достигает максимума. В пределе такое двухмодальное распределение может превратиться в распределение, когда единственно наблюдаемыми погрешностями будут только погрешности ±XmaX (см. рис. 2.4). Например, погрешность от люфта в кинетической цепи, погрешность от гистерезиса имеют вид двухзначной дискретной погрешности.

ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ ЗАКОНОВ РАСПРЕДЕЛЕНИЯ

Статистическое описание случайной величины полным указанием законов распределения слишком громоздка. На практике достаточно указать только отдельные числовые характеристики закона распределения случайной величины. Для оценки того или иного свойства законов распределения случайной величины в теории вероятностей используют числовые характеристики, называемые моментами.

Прежде всего, нас интересует положение случайной величины на числовой оси, т.е. ее систематическая составляющая - ее среднее значение, определяющее положение области, в которой группируется значения случайной величины.

Такое среднее значение случайной величины называется ее первым моментом или ее математическим ожиданием.

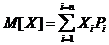, (2.4)

т.е. определяется как сумма произведений всех возможных значений дискретной случайной величины Х на вероятность этих значений Р.

Для непрерывной случайной величины выражение для математического ожидания можно записать

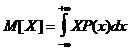, (2.5)

где ×P(X) - плотность распределения вероятностей случайной величины Х.

В отличие от среднего арифметического значения, которое само является случайной величиной, т.к. зависит от испытаний, математическое ожидание является числом, которое связано только с законом распределения случайной величины.

Начальный момент s-го порядка дискретной случайной величины запишется:

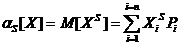
Для непрерывной случайной величины:

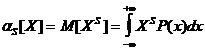
Иначе, математическое ожидание - это начальный момент первого порядка. Случайная погрешность (случайное отклонение) определяется зависимостью:

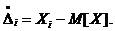
Центральным моментом S-го порядка случайной величины называется математическое ожидание S степени соответствующей центрированной величины.

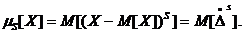
Из определения следует, что m1 = 0, т.е. математическое ожидание первой степени центрированной случайной величины всегда = 0.

Второй центральный момент называется дисперсией случайной величины и характеризуется рассеяние значений случайной величины вокруг математического ожидания.

m2 = D = M)2],

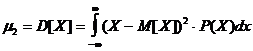
Так как дисперсия имеет разность квадрата случайной величины, то она выражает как бы мощность ее рассеяния. Для наглядной характеристики самой величины рассеяния пользуются среднеквадратическим отклонением случайной величины Х, которое равно 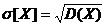и имеет размерность самой случайной величины.

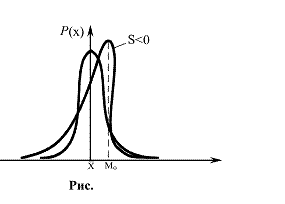
Третий центральный момент характеризует асимметрию, или скошенность (рис. 2.5.) распределения (медиана распределения). Для всех симметричных относительно математического ожидания законов распределения этот момент равен нулю.

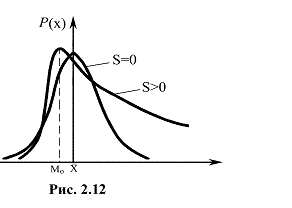
Рис. 2.5. Иллюстрация «скошенности» закона распределения

Медианой непрерывной случайной величины называется такое значение Х, что в этой точке функция распределения F(X) случайной величины Х равна ½.

Для относительной характеристики асимметрии обычно пользуются коэффициентом асимметрии: S = m3/s3

Четвертый центральный момент служит для описания островершинности или плосковершинности распределения (мода). Мода - для дискретной случайной величины - наиболее вероятное значение случайной величины. Мода - для непрерывной - точка максимума плотности распределения ее вероятностей.

Эти свойства описываются с помощью относительного значения четвертого момента, равного m4/s4 , или так называемого эксцесса, который находится как:

Ex = m4/s4 -3

Для нормального закона распределения величина m4/s4 =3, Ex = 0, остальные распределения сравниваются с нормальными, поэтому вычитается тройка. Для нормального закона Ех = 0. Кривые более островершинные по сравнению с нормальным законом, обладают положительным эксцессом, а плосковершинные кривые - отрицательным эксцессом. Точкой перегиба кривой имеют абсциссы

, .

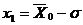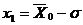Асимметрия, вычисленная по формуле S = m3/s3 = 0. Этот результат характеризует симметричную форму кривой относительно среднего значения Хо, совпадающее с модой Мо и Мс. Эксцесс найденный по формуле Ex= m4/s4-3 = 0.

Функция нормального распределения определяется интегралом

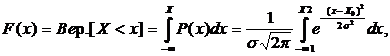
Вероятность нахождения случайной величины Х между X1 и X2 определяется разностью соответствующих значений функции распределения

Вер. = F(X2) - F (X1) = .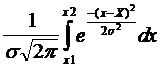

Графически эта вероятность представлена площадью под кривой, изображающей плотность вероятности между ординатами, соответствующими абсциссам X1 и X2.

Если X1 = - ¥ , а X2 = + ¥, то вероятность, определенная по этой формуле обратится в 1 и выразит всю площадь под кривой.

Для облегчения пользования функцией нормального распределения применяют нормированную функцию Лапласа, называемую также интегралом вероятностей

.

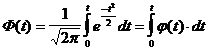Тогда формула запишется

Вер = Ф (t2) - Ф (t1) =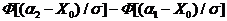

Точность измерения величины x будут определять границы , внутри которых может находится действительное число Х, т.е.

Xo - a X Xo + a,

Где Xo - результат измерения, a - границы интервала

Вероятность того, что действительное значение измеряемой величины Х лежит внутри доверительного интервала (Xo - a, Xo + a) называется надежностью b при заданной точности. При уменьшении доверительного интервала до величины a 2s, надежность результата резко падает. Величину a = 3s, имеющую надежность 99,73%, (доверительная вероятность 0,997) называют предельной погрешностью.

Оценка результатов измерений. Результат всякого измерения содержит в себе случайную погрешность. Поэтому при всех точных измерениях необходимо не только указывать полученный результат, но и делать оценку качества данного измерения, степени достоверности результата или, как говорят, указывать точность измерения.

При оценке точности надо указать границы интервала (доверительного интервала) в который с определенной вероятностью, (доверительной вероятностью) находится результат измерения.