Расчет приращения энтропии

Энтропия – это такая функция состояния термодинамической системы, дифференциал которой

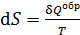. (31)

Здесь 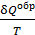– приведенное количество теплоты, где 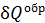– бесконечно малое количество теплоты, сообщаемое телу при температуре T. Из формулы (31) следует, что единица измерения энтропии – 1 .

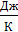Второе начало термодинамики, как закон возрастания энтропии:

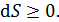
Энтропия замкнутой термодинамической системы возрастает ( 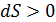),если в системе идут необратимые процессы, и не изменяется( 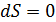)при равновесии. Замкнутой является термодинамическая система, которая не обменивается энергией с окружающей средой, т. е. для нее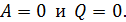

Энтропия незамкнутой системы может изменяться любым образом (убывать, возрастать, оставаться постоянной) в соответствии с формулой (31); например, если 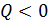, т. е. система отдает теплоту, то и 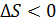, что означает уменьшение энтропии системы, но при 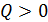величина 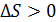и энтропия системы возрастает.

Энтропия является аддитивной величиной: энтропия системы равна сумме энтропий тел, входящих в систему. Например, энтропия смеси двух газов, а также ее приращение 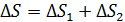, – равно сумме приращений энтропии первого и второго компонентов смеси.

В соответствии с определительной формулой (31) для адиабатного процесса ( 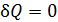) имеем 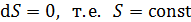; следовательно, обратимый адиабатный процесс протекает при постоянной энтропии. Поэтому адиабатный процесс называют изоэнтропийным.

Расчет приращения энтропии 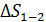при переходе системы из состояния 1 в состояние 2 ведется путем суммирования бесконечно малых приращений 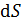с учетом формулы (31):

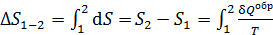, (32)

где величина 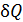, согласно формуле (21):

.

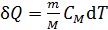В изобарном процессе приращение энтропии

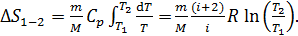(33)

В изохорном процессе аналогично:
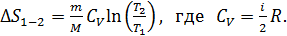(34)

В изотермическом процессе, с учетом первого закона ТД в виде 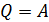и формулы для работы, находим

.

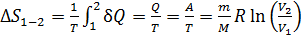При фазовых переходах, протекающих при постоянной температуре T, в соответствии с формулой (32), получаем

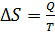, (35)

где 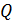– теплота фазового перехода. Например, для плавления льда

,

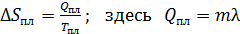где λ – удельная (на 1 кг массы) теплота плавления льда.

Рис. 19

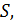
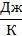
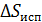
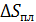
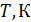
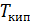
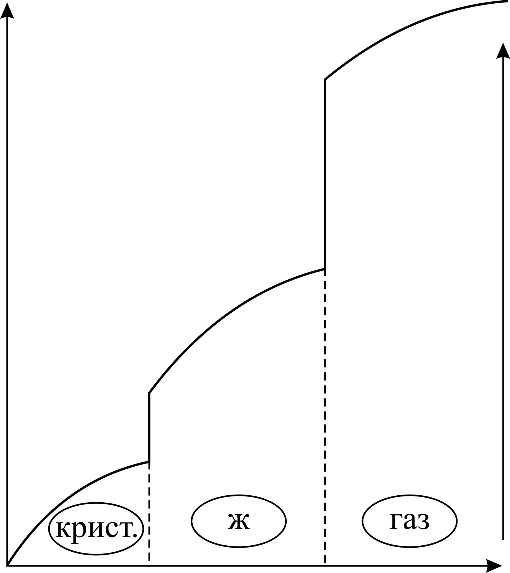Результаты расчета по формулам (34) и (35) показаны на графике (рис. 19). График зависимости 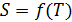начинается практически в точке (0;0), так как третье начало термодинамики (теорема Нернста– Планка) утверждает, что энтропия всех тел стремится к нулю при приближении температуры 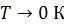. В направлении, показанном стрелкой (справа от графика 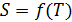), по мере возрастания температуры происходит увеличение энтропии вещества. При этом увеличивается объем системы и с увеличением температуры возрастает скорость движения молекул. Следовательно, растет хаотичность («беспорядок») как в расположении молекул в объеме вещества, так и в движении молекул.