Классическая схема теории вероятностей
Рассмотрим частный случай, когда множество
Ω – пространство элементарных событий, является конечным множеством.
Пусть элементы этого множества (элементарные события) есть 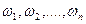 . Согласно схеме §5 любое событие А есть подмножество в Ω, т.е.
. Согласно схеме §5 любое событие А есть подмножество в Ω, т.е.
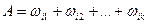
Тогда, поскольку 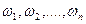 - попарно несовместны, получаем
- попарно несовместны, получаем
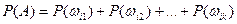 . (1)
. (1)
Значит, чтобы знать вероятность события А надо знать 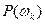 - вероятности элементарных событий.
- вероятности элементарных событий.
Рассмотрим частный (классический) случай когда все числа 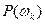 равны между собой:
равны между собой: 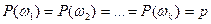 . Другими словами, все элементарные исходы (события) опыта равновероятны. Тогда, поскольку
. Другими словами, все элементарные исходы (события) опыта равновероятны. Тогда, поскольку
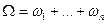 -достоверное событие,
-достоверное событие,
получаем
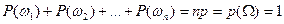
и значит 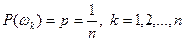 .
.
Значит из формулы (1) получаем: если событие А представляется в виде суммы к равновероятных элементарных событий, то его вероятность будет равна
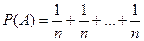 (к - слагаемых)
(к - слагаемых)
Или
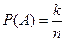 . (2)
. (2)
Формула (2) позволяет решать многие задачи для нахождения вероятностей. В соответствии со сказанным, её применяют в тех случаях, когда для данного опыта можно указать группу из конечного числа событий 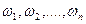 со следующими свойствами:
со следующими свойствами:
1. В результате опыта каждый раз наступает одно и только одно из этих событий
2. Указанные события по условиям данного опыта равновероятны.
При выполнении этих условий вероятность события А вычисляется по формуле (2)
Обычно события 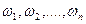 - называют элементарными исходами (случаями), а те элементарные исходы, которые в сумме составляют А, называют благоприятными исходами для события А. В этой терминологии формула (2) читается так: вероятность события А равна отношению числа благоприятных для события А исходов к числу всех (элементарных) исходов.
- называют элементарными исходами (случаями), а те элементарные исходы, которые в сумме составляют А, называют благоприятными исходами для события А. В этой терминологии формула (2) читается так: вероятность события А равна отношению числа благоприятных для события А исходов к числу всех (элементарных) исходов.
Пример 1. В урне находятся 10 шаров: 4 белых и 6 чёрных. Из урны наудачу извлекают шар. Какова вероятность, что он окажется чёрным ( событие А)
Решение: Представим себе, что шары снабжены номерами 1,2,…,10. Обозначим через 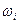 следующее событие: извлечение шара с номером i . Тогда события
следующее событие: извлечение шара с номером i . Тогда события 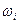 будут элементарными исходами. Действительно, при каждом осуществлении опыта, наступает одно и только одно из них, а слово « наудачу» в формулировке задачи служит указанием на то, что все события
будут элементарными исходами. Действительно, при каждом осуществлении опыта, наступает одно и только одно из них, а слово « наудачу» в формулировке задачи служит указанием на то, что все события 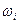 равновероятны. Интересующему нас событию А благоприятны шесть исходов. Значит в данном случае n=10, k=6 и значит
равновероятны. Интересующему нас событию А благоприятны шесть исходов. Значит в данном случае n=10, k=6 и значит 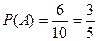 .
.
Замечание. При решении этой задачи мы использовали подробные (громоздкие) рассуждения. При соответствующем навыке можно рассуждать короче, например, так: из 10 возможных случаев событию А благоприятны 6, следовательно, 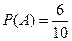 .
.
Дата добавления: 2021-01-11; просмотров: 663;











