Формула сложения вероятностей

Как правило, вероятности различных событий стараются подсчитать косвенным путем, не прибегая к эксперименту (поскольку серию из большого числа опытов трудно осуществить практически). Теория вероятностей устанавливает такие связи между вероятностями случайных событий, которые позволяют вычислять вероятности сложных событий по вероятностям более простых событий.

Выведем одну из основных формул теории вероятностей – формулу сложения вероятностей.

Пусть опыт, с которым связаны события А и В, повторен N раз и пусть при этом N(A) раз наступило событие А и N(B) – событие B. Тогда нетрудно видеть, что имеет место соотношение

N(A+B)=N(A)+N(B)-N(AB)

Разделив обе части равенства на N и взяв предел при 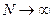( см §2), получим:

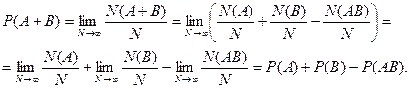
Таким образом, мы получили формулу

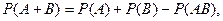(1)

называемую формулой сложения вероятностей.

Найдём вероятность невозможного события Ø.

Имеем N(Ø)=0, значит

.

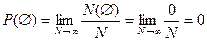Итак, вероятность невозможного события равна 0.

Теперь если события А и В несовместны, то тогда АВ=Ø и значит Р(АВ)=0 . Отсюда из формулы (1) получаем.

Если события А и В несовместны, то тогда

. ( )

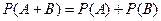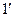Если I – достоверное событие, то тогда N(I)=N и значит

.

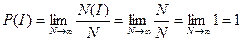Итак, вероятность достоверного события равна 1, т.е.

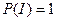. (2)

Далее из того, что А и 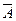несовместны и А+ 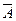=I, то из формул ( 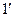) и (2) получаем:

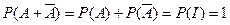
и значит

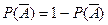, (3)

т.е. получили формулу для вероятности противоположного события.

Нетрудно видеть, что если события 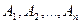попарно несовместны, то справедливо равенство

( )

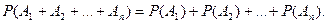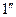Из определения вероятности также следует, что для любого события А имеет место неравенство

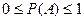. (4)

Действительно, так как 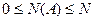, то значит

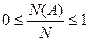. Переходя к пределу при 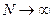получим неравенство (4).