Оценка погрешностей измерений физической величины

ТЕОРИЯ ПОГРЕШНОСТЕЙ

Целью любого исследования является установление связи между различными явлениями и параметрами. В большинстве случаев исследователь стремится установить количественную зависимость между изучаемыми величинами. Установление количественной зависимости невозможно без проведения измерений.Измерение – это сравнение физической величины с некоторой другой, принятой за единицу. Результат измерений выражается числом, показывающим, сколько используемых единиц или долей единицы содержится в измеряемой величине. Выбор единицы измерения диктуется практическими соображениями, но, конечно, не может устанавливаться каждым исследователем независимо от других. Для унификации исследований и придания им свойства сравнимости в физике существует несколько систем единиц. Наиболее употребительной в настоящее время является Международная система единиц (СИ).

Рассмотрим простой пример. Допустим, нам надо измерить массу тела и его объем. Для измерения массы мы используем весы и с их помощью устанавливаем массу тела. Для измерения объема опустим тело в мензурку с жидкостью и измерим, насколько увеличился объем жидкости. Это прямые измерения. Но как измерить плотность тела? Можно, конечно, вырезать из тела, к примеру, один кубический сантиметр и взвесить его. Однако проще сначала измерить массу тела и его объем, а потом разделить полученное значение массы тела на его объем. В этом случае мы непосредственно не измеряем плотность тела, а получаем ее как результат прямых измерений других величин, в данном случае - массы и объема. Такие измерения называются косвенными.

При измерении любой величины мы никогда не получаем истинного значения этой величины. Это объясняется как принципиально ограниченной возможностью точности измерений, так и природой самих измеряемых объектов. Следовательно, в результате измерений получают не истинное значение измеряемой величины, а значения, в той или иной мере отличающиеся от него. Любое измерение проводится с той или иной погрешностью. Естественно, каждый исследователь стремится свести погрешность измерения к минимуму. Что для этого надо делать? Для ответа на этот вопрос рассмотрим, какие бывают погрешности.

Погрешности прямых измерений.Различают четыре типа погрешностей измерений:

1) грубые (промахи);

2) систематические;

3) инструментальные;

4) случайные.

Промахи. Грубые погрешности возникают в результате невнимания или усталости экспериментатора, а также при плохих условиях наблюдения. Грубые погрешности могут возникать в результате действия кратковременного незафиксированного наблюдателем фактора (например, села муха на весы и т.д.). Эти погрешности приводят к оценкам измеряемой величины, резко отличающимся от остальных оценок. Для устранения промахов следует соблюдать аккуратность и тщательность при проведении измерений и составлении протокола измерений. В любом случае грубые погрешности должны быть исключены. Иногда это можно сделать при повторении измерения в несколько иных условиях или другим наблюдателем. Однако и это не всегда позволяет исключить промахи. Далее будет указан критерий, позволяющий отличить промах от иных погрешностей измерения, с помощью расчетов вероятности появления выпадающего значения.

Систематические погрешности характерны тем, что они остаются неизменными по величине во всех измерениях, проводящихся одним и тем же методом с помощью одних и тех же измерительных приборов. В частности, эти погрешности могут возникать из-за того, что в расчетных формулах не учтено влияние некоторых факторов. Так, если при точном взвешивании не учитывается действие выталкивающей силы воздуха по закону Архимеда, то масса тела будет определена неправильно. Такие погрешности можно устранить введением различного рода поправок к расчетным формулам. Систематические погрешности могут быть также обусловлены неисправностью измерительных приборов, у которых, например, смещен нуль. Для того чтобы максимально исключить систематические погрешности, следует тщательно проанализировать метод измерений.

Итак, систематические погрешности появляются при неправильным выборе метода измерений, неправильной установке прибора, либо пренебрежением действия некоторых внешних факторов. Например, погрешности могут возникнуть, если не учитывать теплового расширения при измерениях объема жидкости или газа, производимых при медленно изменяющейся температуре; при измерении массы – если не учитывать действия выталкивающей силы воздуха на взвешиваемое тело и на разновесы; при калориметрических измерениях – если не учитывать теплообмен прибора с внешней средой и т.п. Шкала линейки может быть нанесена неточно (неравномерно); положение нуля термометра может не соответствовать нулевой температуре; капилляр термометра в разных участках может иметь разное сечение; электрический ток может не проходить через амперметр, стрелка прибора может не стоять на нуле и т.д. Округляя численную величину до какого-либо приближенного значения, например, полагая p = 3; p = 3,1; p = 3,14; p = 3,142; p=3,1416 и т.п. вместо p=3,14159265…, мы допускаем систематическую погрешность.

Таким образом, систематические погрешности вызываются определенными причинами. Величина их либо при всех повторных измерениях остается постоянной (как в случаях округления или смещения нуля шкалы прибора и т.п.), либо изменяется по определенному закону (как в случаях неравномерности шкалы, неравномерности сечения капилляра термометра и т.п.). Так как причины, вызывающие систематические погрешности, в большинстве случаев известны, то эти погрешности в принципе могут быть исключены (изменением метода измерений, введением поправок к показаниям приборов, сравнением показаний приборов с показаниями эталонных приборов, благлдаря учету систематического влияния внешних факторов и т.д.), хотя на практике этого не всегда легко добиться.

К инструментальным погрешностям, или погрешностям измерительных приборов, относятся погрешности, возникающие из-за несовершенства средств измерений. Эти погрешности определяются классом точности приборов и, вообще говоря, не могут быть полностью исключены при измерениях. Как правило, наибольшая величина их известна. Развитие измерительной техники привело к появлению разнообразных приборов, отличающихся своей точностью. Точность прибора – это свойство измерительного прибора, характеризующее степень приближения показаний данного измерительного прибора к действительным значениям измеряемой величины. Она связана с физическим явлением, на основе которого построен метод измерения, и с допусками при изготовлении отдельных частей прибора.

Точность прибора либо задается классом точности прибора, либо указана в паспорте, прилагаемом к прибору. Класс точности часто указывается на шкалах многих измерительных приборов, в виде цифры, обведенной кружком. Класс точности определяет абсолютную приборную погрешность в процентах от наибольшего значения величины, которое может быть измерено данным прибором. Например, амперметр имеет шкалу от 0 до 5 А, и его класс точности 1,0. Абсолютная погрешность измерения силы тока таким амперметром составляет один процент от 5 А, т.е. .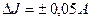

Погрешность, вносимая прибором при каждом отдельном измерении (приборная погрешность), связана с точностью прибора. С понятием абсолютной погрешности, вносимой прибором, связано понятие относительной погрешности. Действительно, если мы будем пользоваться описанным выше прибором, то ошибка в 0,05 А будет вноситься и при измерении силы тока меньше одного ампера и при измерении силы тока в 5 ампер. Ясно, что измерения, проводимые во второй половине шкалы, будут более точны. Чтобы превратить эти интуитивные представления в точные математические, вводят понятие относительной приборной погрешности как величины, численно равной отношению абсолютной приборной погрешности к величине измерения и умножают это отношение на 100%.

Например, пусть первое измерение на нашем амперметре составляет 0,5 А, а второе - 4,5 А. Тогда относительная погрешность в первом случае будет равна: 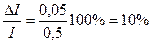, тогда как во втором случае: .

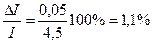Очевидно, можно считать, что второе измерение сделано существенно точнее. Отсюда следует правило, согласно которому проведение измерений надо планировать так, чтобы отсчеты проводились во второй половине шкалы прибора. Никогда не взвешивайте купленные вами несколько килограммов картошки на весах, предназначенных для взвешивания грузовиков с картошкой!

Если класс точности прибора не указан, то абсолютная приборная погрешность равна той доле деления шкалы прибора, до которой с уверенностью в правильности результата можно производить отсчет. Обычно, если нет оговорок в паспорте прибора, она равна цене наименьшего деления шкалы (точнее, ± 0,5 цены наименьшего деления). Естественно, чем точнее прибор, тем меньше его погрешность. Повышая точность отсчета по шкале данного прибора, мы принципиально не можем изменить (увеличить) точность самого прибора. Например, производя измерения длины карандаша с помощью линейки (грубого прибора), разделенной на сантиметры, мы не изменим точности линейки, если будем рассматривать ее шкалу с помощью лупы. Действительно, несмотря на то, что при отсчете с помощью лупы мы легко можем сделать, чтобы в нем содержалось большее число значащих цифр, точность результата измерения длины карандаша останется прежней, так как точность линейки не изменилась. Отсюда следует эмпирическое правило, согласно которому измерения надо производить не более чем на один десятичный знак больше, чем позволяет точность прибора. Таким образом, после округления мы получим значение, согласующееся с абсолютной точностью прибора. Нет никакого смысла, например, как в примере измерения плотности вещества делить массу на объем до получения 5 знаков после запятой, если весы гарантируют правильность только одного знака после запятой.

Случайные погрешности являются следствием действия таких факторов, влияние которых невозможно учесть. Таких факторов много, и роль их при каждом измерении неодинакова. Такие погрешности отличаются друг от друга в отдельных измерениях, и эти различия имеют случайную, неизвестную нам величину. Следовательно, даже в гипотетическом случае, когда первые три вида погрешностей сведены к нулю, точно измерить случайную величину нельзя (исключение составляют лишь те случайные величины, которые имеют дискретный характер: например, число опоздавших студентов или число выученных студентом билетов и т.д.).

Итак, если первые три вида погрешностей могут быть проанализированы или еще до проведения измерения, или могут быть обнаружены и сведены к минимуму после проведения эксперимента, что позволит провести повторные измерения более точно, то случайные погрешности принципиально не устранимы. Неудивительно, что они вызывают наибольший интерес у исследователей.

Правила определения случайных погрешностей рассматриваются в теории погрешностей, основанной на теории вероятностей, позволяющей по данным измерений вычислить наиболее вероятное значение измеряемой величины и оценить погрешность измерений.

Проведение измерений. При измерении любой физической величины обыкновенно приходится выполнять три последовательные операции:

1) проверку и установку приборов;

2) наблюдение показаний приборов и отсчет;

3) вычисление искомой величины из результатов измерений и оценку погрешностей.

Очевидно, что на первом этапе, с точки зрения уменьшения погрешности измерений, мы пытаемся свести к приемлемому уровню инструментальные ошибки и частично исключить возможные систематические ошибки (например, проверяя установку нуля прибора). Как показано выше, полностью свести к нулю инструментальные ошибки практически невозможно.

На втором этапе, проводя измерения внимательно и аккуратно, мы уменьшаем вероятность появления промахов.

Перейдем к третьему, наиболее интересному, этапу: вычислению искомой величины из результатов измерений и оценки погрешностей. Из предыдущего рассмотрения уже должно быть ясно, что результат измерения дает нам не истинное значение измеряемой величины, а лишь приближенное. Для расчета «лучших» оценок истинного значения измеряемой величины нужно принять некоторые предварительные условия, подтверждаемые как опытом, так и теоретическим рассмотрением, которые позволяют дать конкретное наполнение понятию «лучшие» и подсказать механизм расчета этих оценок. Обычно этих условий четыре:

1) погрешности измерения принимают непрерывный ряд значений;

2) при большом числе измерений одинаковые погрешности, но противоположного знака, равновероятны;

3) с увеличением погрешности вероятность ее уменьшается;

4) среднее арифметическое значение является наиболее вероятным значением измеряемой величины.

При таком наборе условий случайные погрешности подчиняются нормальному закону распределения, который изучался в курсе математики в первом семестре (см. методическое пособие по математике и конспект лекций по математике). Необходимо подчеркнуть, что возможны и другие виды распределения случайных погрешностей измерений, но нормальный закон встречается наиболее часто. Кроме того, его особое значение определяется следующим обстоятельством: если случайная погрешность появляется в результате совместного действия нескольких причин, каждая из которых вносит малую долю в общую погрешность, то по какому бы закону ни распределялись погрешности, вызванные каждой из причин отдельно, результат их суммарного действия приведет к нормальному закону распределения случайной результирующей погрешности.

Невозможность получения точного значения измеряемой величины приводит к необходимости определения не только точечных значений этой величины (например, среднего арифметического значения), но и интервальных оценок. Наиболее распространенные интервальные оценки - это абсолютная погрешность отдельного измерения, средняя арифметическая погрешность и доверительный интервал. Точное определение этих понятий мы дадим ниже. Здесь же отметим, что из четырех приведенных выше условий получения «лучших» оценок следует, что чем больше измерений мы произведем, тем точнее будет полученный нами результат и, следовательно, меньше интервальные оценки.

Пусть проделано п измерений некоторой величины х. В результате получен ряд значений этой величины: х₁, х₂, …, х_п. Наиболее вероятным является среднее арифметическое значение этой величины :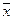

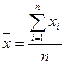(1).

Случайные погрешности измерений 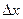распределены по нормальному закону. Величина

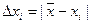(2).

называется абсолютной погрешностью отдельного измерения. Среднее арифметическое значение абсолютных погрешностей отдельных измерений называется средней абсолютной погрешностью

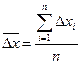(3).

Чтобы ввести еще один показатель качества измерений, рассмотрим еще один раз пример с измерением плотности вещества. В данном случае мы измеряем массу и объем. Очевидно, что конечный результат не может быть получен с точностью большей, чем точность самого грубого измерения. Но масса измеряется в килограммах, а объем – в кубических дециметрах (литрах), поэтому по средней арифметической погрешности, которые имеют ту же размерность, решить вопрос, что измерено с большей точностью нельзя (для этого необходимо уметь определять, что больше, 1 кг или 1 литр!).

Допустим, измерив несколько раз массу тела и рассчитав среднюю арифметическую и среднюю арифметическую погрешность, мы получили следующие значения: 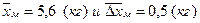. Соответственно для объема мы получили следующие значения: 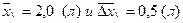. Возникает вопрос: какое из этих измерений мы произвели более точно? Для ответа на подобного рода вопросы вводят понятие относительной погрешности. Итак, относительной погрешностью Е, определяющей качество результатов измерения, называют отношение средней арифметической погрешности к среднему арифметическому значению измеряемой величины, умноженному на 100%:

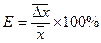(4).

Используя понятие относительной погрешности, легко рассчитать, что в случае измерения массы она равна 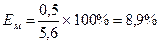, тогда как в случае измерения объема 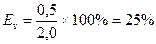. Очевидно, что измерения объема проведены с гораздо меньшей точностью, чем измерения массы.

В процессе изложения материала этого раздела мы уже ссылались на нормальный закон распределения случайной величины. Из курса математики мы знаем, что этот закон определяется двумя параметрами: математическим ожиданием и дисперсией или среднеквадратичным отклонением. Также в курсе математики мы научились рассчитывать выборочные оценки этих величин. Выборочной оценкой математического ожидания является средняя арифметическая, расчет которой проводится по формуле (1). Напомним формулы, по которым рассчитываются выборочные оценки дисперсии и среднеквадратического отклонения:

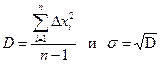(5).

Здесь: D – выборочная оценка дисперсии, 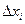– абсолютные ошибки измерений (см. формулу 2), n – число измерений случайной величины, 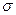– выборочная оценка среднеквадратичного отклонения.

Напомним также, что эти оценки называются выборочными потому, что в любом исследовании, связанном с измерением случайной величины, мы имеем дело с выборкой из генеральной совокупности, число элементов которой предполагается бесконечным. Числовые характеристики выборки и генеральной совокупности будут разными, поскольку в выборке всегда представлена только часть генеральной совокупности. Числовые характеристики разных выборок из одной и той же генеральной совокупности также будут различаться, что объясняется неоднородностью состава выборок.

Представим себе, что мы сделали m выборок из генеральной совокупности, каждая объемом n измерений. Если в каждой из них мы теперь по формуле (1) найдем среднее арифметическое, то получим ряд значений объемом m. Это также будет выборкой (мы ведь могли сделать не m выборок, а произвольно большое число). Для полученной выборки по тем же формулам мы можем рассчитать приведенные выше числовые характеристики, в том числе и среднеквадратичное отклонение для среднеарифметических значений, полученных m выборок. Это среднеквадратичное отклонение называется стандартной ошибкой средней арифметической и обычно обозначается в биологии и медицине буквой m (читается «м малое», в отличие от среднеарифметической, которая обычно обозначается буквой М и читается «М большое»).

Расчеты показывают, что

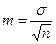(6).

Пришла пора дать ясные интерпретации введенных в рассмотрение величин. Итак, среднеарифметическое выборки, которое рассчитывается по формуле (1), есть наилучшая оценка математического ожидания генеральной совокупности, которую мы можем получить, проведя ряд измерений. Нужно помнить, что она является именно оценкой, а не точным значением, но лучшей оценки по имеющимся данным мы получить не можем. О чем говорит оценка 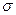, вычисленная по формуле (5)? Это значение позволяет нам оценить степень разброса последовательных измерений. Так, если мы провели, например, 10 измерений и по формуле 5 рассчитали 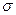, то мы можем делать следующие выводы: следующее (одиннадцатое) измерение с вероятностью 68% попадет в интервал 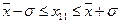, с вероятностью 95% попадет в интервал 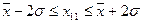и с вероятностью 99,7% – в интервал 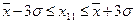. Поскольку интервал в 3 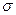дает практически 100% уверенность, на этом построено правило исключения промахов (правило 3 ).

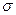Если у вас появилось сомнение, что какое-то из ваших измерений является промахом, уберите его из выборки, рассчитайте по полученному ряду значений 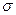, постройте интервал в 3 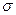. Если убранное из выборки значение лежит за пределами этого интервала, можно смело удалить его из выборки, считая промахом. Если это значение попадает в интервал, необходимо вернуть его в выборку. Оценка m, полученная по формуле (6), является стандартной ошибкой средней арифметической и играет ту же роль для ряда, составленного из нескольких значений средних арифметических, что и 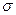для первичного ряда измерений.

В приведенном выше примере мы впервые сталкиваемся с одним из важнейших принципов статистического вывода. Ведь мы делаем вывод об удалении (или нет) из выборки того или иного значения на основании учета вероятности правильности наших действий. Приведем еще один пример. Выше мы отмечали, что средняя арифметическая является лучшей оценкой математического ожидания генеральной совокупности, и мы не можем получить точное значение математического ожидания генеральной совокупности. А что мы можем? Мы можем указать интервал, в котором с определенной вероятностью находится это значение. Ключевыми словами в предыдущем предложении является слова «с определенной вероятностью». Это подразумевает, что мы должны задать эту вероятность априори (до опыта). Если мы задаем ее, то именно с этой вероятностью мы и будем делать все выводы, которые можно получить из наших измерений. Неудивительно, что эта вероятность называется уровнем достоверности наших выводов. Самый низкий уровень достоверности в биологии и медицине принимается равным 0,95.

Поставим следующую задачу: необходимо рассчитать интервал, в котором с вероятностью 0,95 находится истинное значение математического ожидания. Эту задачу мы решали в курсе математики (см. учебное пособие по математике). Здесь же напомним формулу, по которой проводятся расчеты:

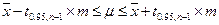(7) или

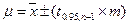(8).

В формулах (7 и 8) 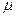- это математическое ожидание, а t_0.95,n-1 – значение коэффициента Стьюдента для доверительной вероятности 0.95 и числа измерений n. Коэффициенты Стьюдента можно получить в таблице 4 приложения к учебному пособию по математике.

Можно поставить и обратную задачу. Предположим, мы изучаем влияние высокогорья на нагнетательную функцию сердца у человека. Для этого мы измеряем ударный объем сердца (объем крови, выбрасываемый сердцем за одно сокращение) у 8 человек в условиях равнины, а затем - через три месяца пребывания этих же людей на высоте 3000 метров над уровнем моря. В результате измерений мы получаем две выборки. Для каждой из них рассчитываем оценки среднего арифметического и среднеквадратичной ошибки среднего (m, см. формулу (6)). Сравнивая оценки среднего арифметического на равнине и высокогорье ( 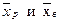) мы, конечно, отметим, что они различаются. Но является ли это различие достаточным, для того, чтобы сделать вывод о том, что адаптация к высокогорью изменяет нагнетательную функцию сердца?

Обычный алгоритм решения этой задачи такой. Строится, как говорят, нулевая гипотеза. В нашем случае она может выглядеть следующим образом. Н₀: адаптация к высокогорью существенно не изменяет нагнетательную способность сердца. После этого рассчитывается уровень достоверности для этой гипотезы. В случае сравнения средних арифметических этот расчет проводится следующим образом:

Рассчитывается экспериментальный коэффициент Стьюдента по формуле:

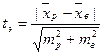(8).

Потом с этим коэффициентом входим в ту же таблицу Стьюдента с числом измерений 2(n-1) (равновеликие выборки) и заданным уровнем достоверности (0,05 или 0,01) и сравниваем полученное значение t_э c табличными значениями. Если полученное нами значение t_э больше табличного, мы делаем вывод, что нулевая гипотеза неверна. В противном случае мы вынуждены принять нулевую гипотезу. Допустим, проведя расчеты по формуле (8), мы получили значение 2,3. Поскольку у нас выборка состоит из 8 человек, смотрим, что стоит на пересечении 14 -й строки таблицы Стьюдента и уровнем достоверности 0,95 (см.: Учебное пособие по математике, с. 84). Там стоит число 2,14. Таким образом, наше число оказывается больше, следовательно, нулевая гипотеза неверна с вероятностью более 0,95. Если же мы зададимся уровнем 0,99, то увидим, что соответствующее значение коэффициента Стьюдента равно 2,98, то есть, больше полученного нами числа. Поэтому, если мы хотим делать выводы с вероятностью не ниже 0,99, мы должны принять нулевую гипотезу.