ТАРАУ. Астрофизика элементтері. 6 глава

Динамикалық шкалалармен өлшенетін уақыт бірқалыпты болып табылатыны жоғарыда айтылды. Бірақ уақыттың идеал бірқалыпты динамикалық шкаласын құру мына себептермен шектеледі: күн жүйесінің құрылысын толығымен білмеу, күн жүйесі денелерін бақылаудың және олардың орындарын есептеу дәлдігінің деңгейі, бақылау мезеттерін анықтаудың дәлдігінің деңгейі.

1.11.10. Атомдық уақыт шкалалары

Атомдық уақыт шкалалары атомдық сағат көрсетуіне негізделген, олардың өлшем бірлігі атомдардың бір кванттық күйінен екіншіге ауысу кезіндегі энергияның сәулену немесе жұтылу жиілігіне байланысты.Сөйтіп, атомдық уақыт жүйелері жиіліктің атомдық эталондарының ашылуына байланысты жасалынған, түбегейлі жаңа, Жер мен аспан денелерінің қозғалысына тәуелсіз уақыт шкалалары.

Халықаралық атомдық уақыт ТАI (Temps Atomic International) жүйесі 1967 жылынан бастап Халықаралық уақыт бюросымен жеке обсерваториялардың атомдық эталондарын салыстыру негізінде есептеледі. Оның өлшем бірлігі – сыртқы магнит өрістер жоқ болғандағы, теңіз деңгейіндегі цезий-133 атомының негізгі күйінің екі асажұқа деңгейі арасындағы ауысудың резонанстық жиілігіне сәйкес келетін сәулеленудің 9 192 631 770 тербелісінің ұзақтығына тең атомдық секунд. ТАI секундының ұзақтығы ол 1900 жылындағы ET эфемеридалық уақыт секундының ұзақтығына тең болатындай етіп қалап алынған. Атомдық секунд эфемеридалық секундке қатысты 2×10^-9 дәлдікпен анықталған. ТАI шкаласындағы уақытты есептеу басы ТАI мен UТ шкалаларындағы сағаттардың көрсетулері 1958 жылдың 1 қантарының 0^h UТ мезетінде бірдей болатындай етіп қалап алынған. Бұл мезет үшін ΔТ= ЕТ- UТ айырмасы +32^s,184 тең болғандықтан, TAI атомдық шкаланың ET шкаламен айырмасы мына қатынаспен беріледі:

ЕТ= ТАI+32^s,184

Зерттеулер көрсеткендей, атомдық эталондармен анықталатын уақыт шакаласы өте тұрақты болып табылады және оңай жүзеге асырылады. 1 айдан 1 жылға дейінгі уақыт аралығы үшін ТАI секунд ұзақтығының тұрақсыздығы 10^-14 тең (не одан кіші). Орталаудың аралықтары үлкендеу болған жағдайда тұрақсыздық ~5×10^-14 дейін өседі.

Цезийліктен басқа жиіліктің сутегілік, рубидийлік, тағы басқа да стандарттары бар. Әр стандарт атомдық уақыттың өзіндік шкаласын анықтайды. Сутегілік стандарттардың қысқамерзімді (100-1000 с аралығындағы) тұрақтылығы цезийлікке қарағанда жоғары болып табылады (тұрақсыздығы 10^-15 аз болады).

Атомдық уақыт астрономиялық бақылаулар мен аспан денелерінің қозғалысына тәуелсіз болғандықтан, сондай-ақ оның көмегімен уақыттың бірқалыпты шкаласын жоғары дәлдікпен оңай жүзеге асырылатындықтан, ол Жердің өз осі бойымен айналуының бірқалыпсыздығын зерттеу негізі болып табылады. Жалпы, айтылған артықшылықтарына байланысты, қазіргі кезде уақыттың атомдық шкаласы астрономияда да, күнделікті өмірде де қолданылатын уақыт шкаласы болып табылады.

Атомдық пен динамикалық уақыт шкалалары бір біріне де, күн мен жұлдыздық уақыт шкалаларына, яғни Жер айналуына, тәуелсіз болып табылады. Бірақ адамның күнделікті өмірі Күннің кульминациясы, шығысы және батысымен, яғни Жер айналуымен тығыз байланысты болғандықтан, астрометрияның маңызды міндеттерінің бірі – атомдық және күн уақыты арасындағы байланысты табу. Бұл есеп тек қана радиокөздерді, жұлдыздарды, күн жүйесінің денелерін жүйелі турде бақылау көмегімен шешілу мүмкін. Бақылаулар күн жүйесінің айнымалы гравитациялық өрісте қозғалып тұрған Жерден жүргізіледі. Сондықтан бақылау мезеттерін атомдық шкаладан динамикалық шкалаларға және кері түрлендірулер қазіргі заманғы сфералық астрономияда Эйнштейннің салыстырмалық теориясы негізінде Жердің жылдамдығы мен күн жүйесінің гравитациялық потенциалын еске алып жүргізіледі.

Пульсарларды ашу, оларды бақылау әдістері мен бақылау нәтижелерін өңдеу теориясын даярлау жаңа шкаланың – пульсарлық уақыт шкаласының құрылуына әкелу тиіс, оның ұзақ уақыт аралықтарындағы тұрақтылығы атомдық уақыттан жоғары болады.

1.12. ЖҰЛДЫЗДАРДЫҢ АСПАН СФЕРАСЫНДАҒЫ ОРНАЛАСУЫН БҰРМАЛАЙТЫН ЭФФЕКТІЛЕР

1.12.1. Астрономиялық рефракция. Астрономиялық рефракция туралы түсінік

Шырақ жарығының Жер атмосферасындағы сыну салдарынан сол шырақтың көкжиекке қатысты көрінетін орналасуы оның шынайы (ақиқат) орналасуынан өзгеше болады.

Жер бетінен үлкен қашықтықта (ауасыз кеңістікте) n сыну көрсеткіші 1 тең, ал жарық жылдамдығы жарықтың вакуумдағы жылдамдығына тең. Атмосферада сыну көрсеткіші 1 тең емес болады, және де ауа тығыздығына байланысты өзгереді. Сөйтіп, Жер атмосферасына түскенде жұлдызбен шығарылған жарықтың сәулелері сыну көрсеткіші өзгеретін орта арқылы өтеді. Бұның нәтижесінде жұлдыз жарығының атмосферадағы жолы түзу болып табылмайды. Сонда, рефракция себебінен бақылаушы нақтылы (атмосфера болмағандағы) зениттік қашықтығы z –ке тең жұлдызды z зениттік қашықтықта көреді. Астрономиялық рефракция деп аспан денесінің жарығы Жер атмосферасын өту нәтижесінде болатын бұл дененің көрінетін орналасуының оның шынайы орналасуына қатысты ығысуын айтады. Бұл ығысудың r бұрышын да астрономиялық рефракция, немесе рефракция бұрышы деп атайды: r = z-z.

1.22 сурет- Рефракция құбылысы

Сыну көрсеткіші жарық сәулесінің траекториясы бойымен қалай өзгеретінін білу үшін ауа тығыздығының өзгеру заңдылықтарын білу қажет. Бірақ тығыздықтың биіктікпен өзгеруінің дәл заңы белгісіз болғандықтан, рефракция мәнің дәл анықтау мүмкін емес. Оптикалық диапазонда рефракция позициялық бақылаулардың дәлдігін шектейтін ең негізгі факторлардың бірі болып табылады. Мәселені шешудің жалғыз тәсілі – оптикалық телескоптарды Жер атмосферасынан тыс шығарып орналастыру. Нәтижесінде ~120000 жұлдыздың дәлдігі жоғары каталогы құрастырылған HIPPARCOS жобаның табысты бітуі бұл қорытындыны растайды. Егер бақылаулар радиодиапазонда жүргізілсе (АҰБР-лерде, немесе серіктерден сигналдар қабылданса), онда радиорефракцияны еске алудың арнайы әдістері қолданылады. АҰБР мен глобальды навигациялық GPS және ГЛОНАСС жүйелері қазіргі заманғы астрометриялық және геодезиялық желістердің негізі болып табылатындықтан, радиорефракцияны еске алудың әдістеріне ерекше назар бөлу керек. Бірақ бұл мәселе арнайы курстарда қарастырылады.

1.12.2. Жазық-параллель атмосферадағы оптикалық рефракция

Рефракцияны еске алудың қарапайым формулаларын Жер атмосферасының параллель-жазықты моделін қарастырып алуға болады. Бұл модельде атмосфера параллель-жазықты қабаттарға бөлінеді, және n сыну көрсеткіші қабат ішінде тұрақты болып, ал қабаттар шекарасында секірмелі түрде өзгереді деп есептелінеді. Жер беті қасындағы сыну көрсеткіші n₀ –ге тең және зениттік қашықтық z тең, ал нөмірі N ең жоғарғы қабатта n сыну көрсеткіші 1-ге тең және зениттік қашықтық z-ке тең.

Сыну заңын (Снеллиус заңын) i -ші және (i+1) –ші қабаттар үшін жазайық:

n_i+1sinz_i+1=n_isinz_i (1.12.1)

i -ші және (i-1) –ші қабаттарүшін:

n_isinz_i=n_i-1sinz_i-1, (1.12.2)

яғни

n_i+1sinz_i+1=n_i-1sinz_i-1 (1.12.3)

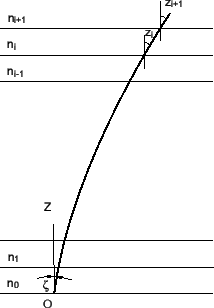
1.22 сурет– Жазық-параллель атмосферадағы рефракция

(1.12.1) теңдеулер тізбегін жалғастыра отырып, мынаны аламыз:

sinz_i=n₀sinz (1.12.4)

Жер беті маңында сыну көрсеткіші 1-ден көп болғандықтан, z<z. Бұл рефракция жұлдызды қашанда да зенитке қарай ығыстыратынын көрсетеді.

Егер сыну көрсеткіші азимутқа тәуелсіз болса, онда жарық сәулесі тік жазықтықтан шықпайды, яғни азимут рефракциямен бұрмаланбайды. z =r +z болғандықтан:

sin(r+z)=n₀sinz (1.12.5)

Рефракцияның мәні доғаның бірнеше минутынан көп болмайтынын, яғни sinr≈r, cosr≈1 екендігін еске алып, рефракцияның радиандағы мәнін аламыз:

r≈(n₀-1)tgz (1.12.6)

Сөйтіп, рефракцияның мәні жұлдыздың зениттік қашықтығы мен Жер беті маңындағы сыну көрсеткішіне тәуелді болады. Жер атмосферасының құрылысын қарапайымдату рефракцияны есептеу үшін тек Жер беті маңындағы сыну көрсеткішін білу керектігін қажеттейді. Жер беті маңындағы сыну көрсеткіші жергілікті метеорологиялық параметрлерге байланысты болады. Қалыпты шарттарда (қысым сынап бағанасының 760 мм –не, ал температура 0^°C тең болғанда ) n₀=1,0002926. Егер k₀=n₀ - 1 белгілеуді енгізсек, онда қалыпты шарттарда k₀=0,0002926=60^’’,343; k₀ коэффициентті кейде рефракция тұрақтысы деп атайды. Егер шарттар қалыптылардан өзгеше болса, онда сыну көрсеткішінің қысым мен температураға тәуелділігінің мынадай заңын қолданады:

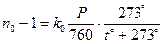, (1.12.7)

мұндағы P- Жер беті қасындағы сынап бағанасының мм түріндегі қысым, 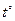- ауаның Цельсий шкаласы бойынша көрсетілген температура.

Іс жүзінде Жер беті маңындағы сыну көрсеткіші тек Жер беті маңындағы қысым мен температураға емес, ауаның құрамына (ең бастысы су буының мөлшеріне) және жарықтың толқын ұзындығына да тәуелді болады. Су буының оптикалық диапазондағы рефракцияға әсері аз ((2) формуланың дәлдігімен салыстырғанда), ал радиодиапазонда айтарлықтай болады. Тропосфераның төменгі қабаттарындағы радиокөз бағытындағы су буының дәл мөлшерін анықтау мүмкін емес болғаны радиоастрономиялық бақылаулар дәлдігін шектейтін негізгі себебі болып табылады. n₀ –ң 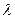толқын ұзындығына тәуелділігі (дисперсия) оптикалық диапазонда да елеулі болады. Жоғарыда келтірілген n₀=1,0002926 мәні шырақтың визуальды көрінерлік жұлдыздық шамасын анықтау үшін қолданылатын V-жолақтың центріне ( 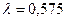микрон) сәйкес келеді. Жалпы түрде (n₀ –1) өрнегінің 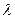-ға тәуелділігін былай жазуға болады:

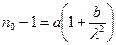, (1.12.8)

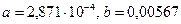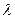мұндағы , ал микрондармен берілген. (n₀ –1) мәні көрінетін спектр аралығында шамамен 2% өзгереді. Рефракция нәтижесінде жұлдыздың бейнесі тік шеңбер бойымен спектрге жіктеледі, спектрдің қызыл шеті көкжиекке жақын орналасады. Бұл кластары әртүрлі жұлдыздарды бақылап (немесе класы бір жұлдыздарды әртүрлі сүзбелерді қолданып бақылап) координаттарды анықтаған кезде n₀–дің 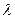-ға тәуелділігімен байланысты жүйелі қателіктер мүмкін екендігін көрсетеді.

1.12.3. Сфералық-симметриялы атмосферадағы оптикалық рефракция

(1.12.4) формула өте жуықталған болып табылады, ол тек атмосфераның параллель- жазықты құрылысы болжау шегінде дұрыс болады. (1.12.4) формуланы егер зениттік қашықтық аз болса ғана пайдалануға болады. z>70⁰ болғанда бұл формула жарамсыз болады. Рефракцияны еске алудың дәлдігі әлдеқайда жоғары формуланы радиалды-симметриялы атмосфераны қарастырып алуға болады.

Бұл модельде атмосфера центрлері Жер центрінде (О нүктесінде) орналасқан жұқа сфералық қабаттарға бөлінеді (сурет), және ауа тығыздығы, демек сыну көрсеткіші де, тек биіктікке (Жер центріне дейінгі қашықтыққа) тәуелді болады.

Жарықтың сыну заңы бойынша i –шi және (i-1)-ші қабаттар шекарасында:

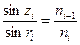(1.12.9)

z_i және r_i бұрыштардың айырмасын 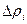деп белгілейік:

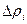= z_i- r_i (1.12.10)

Егер 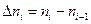, онда

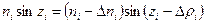(1.12.11)

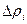шаманың аздығын еске алып, мынаны аламыз:

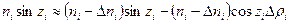(1.12.12)

аздық реті екіге тең 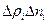мүшесін еске алмасақ, онда:

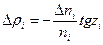(1.12.13)

Барлық 0-ден N-ге дейінгі қабаттар бойынша қосындылап, толық рефракцияның мәнін аламыз:

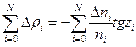(1.12.14)

Әр қабаттың қалындығын азайтып және қабаттардың санын көбейтіп, 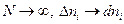, аламыз, ал қосынды интегралға ұмтылады, яғни

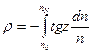(1.12.15)

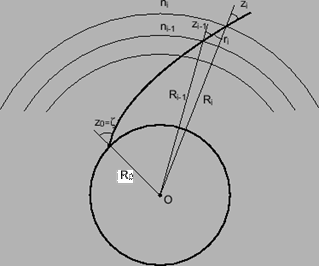
1.23 сурет –Сфералық - симметриялы атмосферадағы рефракция

Интегралдау n=n₀ болғандағы Жер бетінен n=1 болғандағы атмосфераның жоғарғы N қабатына дейін жүргізіледі. Интегралдау шектерін алмастырып:

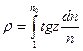(1.12.16)

Сәуленің жолы бойымен z-ң мәні белгісіз болғандықтан, tgz орнына z көрінерлік зениттік қашықтыққа тәуелді функцияны қолдануға болады. Оларды байланыстыратын формуланы қорытусыз берейік:

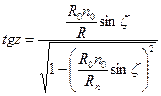(1.12.17)

Онда радиалды-симметриялы атмосферадағы рефракция:

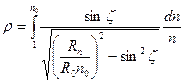(1.12.18)

Бұл формула – дәл формула. Егер n=n(R) функция белгілі болса, онда 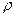рефракцияны санды түрдегі интегралдау арқылы есептеуге болатын еді.

Іс жүзінде (1.12.18)-гі интеграл R/R₀ параметрді 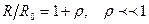қатынасты қолданып қатарға жіктеп есептейді. Бұл атмосфераның қалындығы 100-150 км құрайды деп есептегнде орындалады. Бұл деңгейден жоғары ауа тығыздығы өте аз болады да, оптикалық рефракция жоқ деп айтуға болады.

Шығаруға назар бөлмей, бірден қорытқы формуланы жазып алайық.

R_n, R₀ шамаларының қатынасын В деп белгілесек, рефракция мынаған тең болады екен:

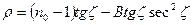(1.12.19)

немесе

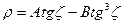, (1.12.20)

мұндағы A=(n₀ - 1) - B. Бұл формула Лаплас формуласы деп аталады.

A және B коэффициенттері бақылау орнындағы Жер беті маңындағы қысымға, температураға, толқын ұзындығына, обсерваторияның теңіз деңгейінен h биіктігіне тәуелді болады. P=1010,25 мбар, t=15^ºС, 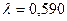мкм, 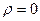болғанда, Лаплас формуласындағы А мен В коэффициенттері мынаған тең: А=57^”,085, B=0^”,0666.

Лаплас формуласы "Рефракцияның Пулков кестелері " негізінде жатыр. Бұл кестелер алғаш рет 1870 ж. жарияланған еді, одан соң олар 1905 ж., 1930 ж., 1956 ж. қайта шығарылды. Кестелерде орташа метеорологиялық шарттар үшін (t=9,3^ºC, P=751,6 мм. сын. бағ., су буының парциал қысымы е=6 мм. сын. бағ.) рефракцияның мәні бақылау шарттарының орташалардан ауытқуды еске алатын түзетулермен бірге келтіріледі.

Үлкен зениттік қашықтардағы (z>75^º) және көкжиекке жақын бақылауларды жүргізгенде дәлдігі жоғары (10) формуланы қолдану керек. Мысалы, көкжиектегі бақылаулар

( z=90^º) жағдайында Пулков кестелерінен рефракция шамамен 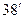-қа тең (P=1013,25 мбар, t=0^ºC, 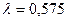мкм). Сонда жұлдыздың шығысы мен батуы мезетінде оның зениттік қашықтығы, z=90^º + 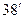. Күн мен Айды бақылаған кезде шығыс пен бату мезеті дегенде олардың жоғарғы шеті туралы айтылады, демек Күн мен Ай центрінің зениттік қашықтығы , z=90^º + 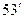( Күн не Ай дискінің радиусын 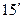тең деп есептейміз). Бату уақыты мына теңдеумен анықталады:

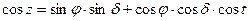(1.12.21)

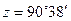(жұлдыздар, планеталар үшін) немесе 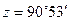Күн мен Айдың жоғарғы шеті үшін) болғанда. Рефракция шығу- бату уақытын бірнеше минутқа өзгертеді, күннің ұзақтығы (Күн көкжиек үстінде болған уақыты) ~ 10 минутқа созылады.

1.12.4. Рефракцияның жұлдыздың тік шарықтауы мен еңкеюіне әсері

Бұл әсерді табу үшін P_NZS параллакстық үшбұрышты қарастырады (1.23 сурет), S- жұлдыздың ақиқат орналасуы деп есептейік. Жұлдыздың зениттік қашықтығы (ZS доғасы) z тең.

Рефракция нәтижесінде жұлдыздың кескіні тік шеңбер бойымен бақылаушының зениті бағытында 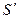S нүктеге ығысады. S нүкте арқылы параллельді жүргізіп, 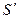нүктеден - 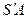параллелге және 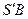еңкеюлер шеңберіне перпендикулярларды түсірейік. 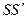доғасы 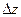пен 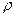рефракцияға тең екендігін, ал 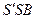және 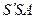үшбұрыштарды жазық деп есептеуге болатындығын еске алып, мынаны жазамыз:

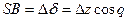(1.12.22)

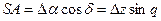(1.12.23)

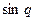мен 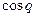мәндерін параллакстық үшбұрыш үшін формулалардан аламыз:

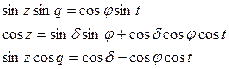(1.12.24)

1.23 сурет- Координаттардың рефракция салдарынан өзгеруі

Онда

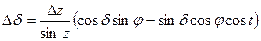
(1.12.25)

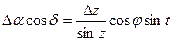(1.12.26)

Жоғарыдағы теңдеулерді қолдансақ: 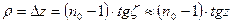, ал қорытқы теңдеулер мына түрде жазылады:

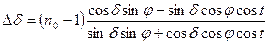(1.12.27)

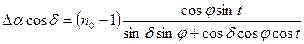(1.12.28)

Бақылаулар меридианда жүргізілгенде sint=0 болады және координаттардың рефракциядан өзгеруі :

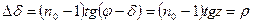(1.12.29)

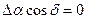
Демек, меридиандық бақылаулар жағдайында рефракция тек жұлдыздардың еңкеюлерін анықтағанда еске алынады.

1.12.5. Аберрация мен параллакстық ығысу туралы жалпы түсінік

Бақылаулар өз өсі бойымен айналатын Жердің бетінен жүргізіледі. Онымен қоса Жер орбита бойымен Күнді айналап қозғалады және Күнмен бірге Галактика центрі бойымен айналады. Жермен бірге бұл қозғалыстарға бақылаушы да қатысады. Олардың (қозғалыстардың) әрқайсысы аспан денелерінің (жұлдыздардың, радиокөздердің, Күн жүйесі денелерінің) шынайы орналасуының өзгеруіне әкеледі.

Жоғарыда айтылғандай, топоцентрлік (центрі бақылаушы орналасқан Жер бетіндегі бір нүктеде жатқан) координаттар жүйесі Жердің өз осі бойымен және Күн бойымен айналуынан байланысты инерциялық болып табылмайды. Сондықтан топоцентрлік жүйеде жүргізілген бақылаулардың нәтижелерін әуелі геоцентрлік (центрі Жер центрінде орналасқан), одан кейін барицентрлік (центрі Күн жүйесінің масса центрінде орналасқан) жүйеге түрлендіреді. Барицентрлік жүйе жүзеге Галактикадан тыс көздер координаттарымен асырылады, сондықтан ол инерциялық жүйеге жақын. Бақыланған координаттардың инерциялық санақ жүйесіне (ИСЖ) түрлендіру топоцентрлік жүйенің қозғалыс жылдамдығын еске алуды және координаттар жүйесінің басын тасымалдауды, яғни бақылаушыны Күн жүйесінің барицентріне тасымалдауды қажет. Санақ жүйесінің қозғалысы салдарынан болатын аспан денелерінің аспан сферасындағы орналасуының өзгеруі аберрация деп аталады. Бақылаушы кеңістіктің басқа нүктесіне өтуі де (координаттар басын жылжытуы) аспан денесіне бағыттың өзгеруіне әкеледі. Бұл эффект параллаксттық ығысу деп аталады. Неғұрлым дене бақылаушыдан алыс болса, соғұрлым оның параллакстық ығысуы аз болатыны түсінікті. Жер қозғалысының үш түрі денелердің аспан сферасындағы орналасу өзгерістернінің (вариацияларының) үш түріне әкеледі: тәуіліктік, жылдық және ғасырлық параллкстық ығысуы мен аберрацияға.