ТАРАУ. Астрофизика элементтері. 8 глава

1.12.12. Оптикалық бақылауларды редукциялау

Аспан санақ жүйесі координаттары аспан сферасындағы жүйенің негізгі нүктелер мен шеңберлерін бекітетін таңдап алынған жұлдызардың (немесе радиокөздердің) тізімімен жүзеге асырылуы мүмкін. Тірек жұлдыздар тізімі іргелі каталог деп, ал аспан жүйесі іргелі жұлдыздық жүйе деп аталады. Тірек жұлдыздардың координаттары (тік шарықтау мен еңкеюі) бірнеше себептен өзгереді. Біз жұлдыздардың орналасуы меншікті қозғалысынан, аберрация, параллакстық ығысу, рефракция себебінен қалай өзгеретінін қарастырдық. Сондай-ақ біз аспан экваторының қозғалысына, демек жұлдыздар координаталарын өзгеруіне де әкелетін прецессия мен нутацияны қарастырдық. Бұл себептерден санақ жүйесінің негізгі шеңберлерін бекіту үшін жұлдыздар координаттары белгіленген дәуірді анықтау, санақ жүйесінің басын көрсету және аспан экваторы мен көктемгі күн мен түннің теңелу нүктесінің орналасуын анықтау керек.

Жоғарыда айтылғандай, экватор мен күн мен түннің теңелуі нутация ескерілуіне не ескерілмеуіне байланысты ақиқат немесе орташа деп аталанады. Стандарт дәуір ретінде қазір J2000.0 дәуірі белгіленген.

Жұлдыздың орташа орны деп оның бақыланған күндегі орташа экваторға және күн мен түннің теңелуіне қатыстырылған (қатысты анықталған) барицентрлік санақ жүйесіндегі координаттарын атайық. Жұлдыздың орташа координаттары прецессия мен меншікті қозғалысы салдарынан өзгереді, орташа координаттарының анықтамасы бойынша басқа эффекттер шығарып тасталған (ескерілген).

Жұлдыздың көрінетін орны деп бақылау күні үшін белгілінген ақиқат экватор мен күннің және түннің теңелуіне қатыстырылған геоцентрлік санақ жүйесіндегі жұлдыздың координаттары аталады. Орташа орыннан көрінетін орынға түрлендіру нутацияны, жылдық аберрацияны және параллакстық ығысуды еске алуды кіргізеді. Жұлдыздың көрінетін кординаттары бақыланатын координаттарынан рефракция мен тәуіліктік аберрацияны еске алатын түзетумен айыралады.

Каталогтарда жұлдыздардың стандарт дәуірі үшін анықталған жұлдыздардың орташа орындары келтіріледі. Демек, орташа орындардан орташа стандартты орындарға ауысу үшін прецессия мен меншікті қозғалысты еске алуға керек. HIPPARCOS каталогында жұлдыздар координаттары J1991.25 дәуірге келтірілген, ал HIPPARCOS жүйенің экваторы J2000.0 экваторымен беттеседі. Демек, жұлдыздың координаттарын стандарт дәуірге түрлендіру үшін тек меншікті қозғалысты еске алу керек.

Егер жұлдыз, немесе планетаның өлшенген координаттарын стандарт дәуірдің экваторы мен күннің және түннің теңелуіне түрлендіру керек болса, онда оптикалық астрометриялық бақылауларды өңдеудің классикалық әдісі мынадай болады

1. Бақыланған зениттік қашықтықтардан рефракцияға түзетулер алынады да, атмосферасы жоқ Жер бетіндегі нүкте үшін аспан денелерінің тік шарықтаулары мен еңкеюлері анықталады.

2. Тәуіліктік аберрациямен байланысты түзетулерді еске алып, айналмайтын Жерге қатысты координаттары табылады.

3. Тәуіліктік параллаксты еске алу санақ басын Жер центріне тасымалдауға әкеледі. Аспан денесінің геоцентрлік орналасуы, жоғарыда айтылғандай, көрінетін орны деп аталады.

4. Жылдық аберрацияны (жақын денелер үшін – планеталық аберрацияны) еске алу координатар басын барицентрге тасымалдауға әкеледі. Жасалынған редукция нәтижесінде аспан денелерінің координаттары бақылау күндегі ақиқат экватор мен күннің және түннің теңелуіне қатысты барицентрлік санақ жүйесінде анықталады.

5. Нутацияны еске алу арқылы бақылау күндегі орташа экватор мен күннің және түннің теңелуіне қатысты координаттар анықталады.

6. Координаттарды прецессия мен меншікті қозғалысқа түзетіп, стандарт дәуірдің орташа экваторы мен күннің және түннің теңелуіне қатысты координаттарды аламыз. Бұл координаттар жүйесіндегі аспан денелерінің орналасуы стандарт орташа орын болып табылады.

Толығырақ редукция процедурасы арнайы курстарда қарастырылады

ТАРАУ

АСПАН МЕХАНИКАСЫНЫҢ ЭЛЕМЕНТТЕРІ

2.1. Планеталардың көрінетін және нақты қозғалысы

2.1.1. Планеталардың көрінетін қозғалысы

Планеталар көрінетін қозғалыстары бойынша 2 топқа бөлінеді: төменгі (Меркурий, Шолпан) және жоғарғы (Жерден басқа қалған планеталар).

Төменгі және жоғарғы топ планеталарының шоқжұлдыздардағы қозғалыстары түрліше. Меркурий және Шолпан әрқашан Күн қай шоқжұлдызда орналасса, олар да сол немесе көршілес шоқжұлдызда орналасады. Олар Күннен шығыс немесе батысқа қарай орналасуы мүмкін. Планеталардың Күннен шығысқа қарай ең үлкен бұрыштық алшақтауы – ең үлкен шығыстық элонгация, ал батысқа қарай ең үлкен бұрыштық алшақтауы – батыстық элонгация деп аталады. Шығыстық элонгация кезінде планета батыстан Күн батқаннан кейін көрінеді және Күннен кейін аз уақыттан соң батады. Содан кейін кері қарай қозғалады. Алғашында жәй, кейін қатты қозғалып Күнге жақындайды, төменгі бірігу процесі басталады. Біршама уақыттан соң планета қайта көрінеді, Күннен алшақтай бастайды да ең үлкен батыстық элонгацияға жетеді. Планета тоқтап, тік қозғалады, енді ол батыстан шығысқа қарай қозғалады, Күннен қашықтау қысқарады. Бұл уақытта планета Күннің артынан өтеді, екеуінің эклиптикалық бойлықтары тең болады – бұл Күн мен планетаның жоғарғы бірігуі деп аталады. Әрі қарай планета қайтадан батыста көрінеді, яғни төменгі планеталар Күн маңайында тербелетіндей болып қозғалыс жасайды.

Ал, жоғарғы топ планеталарының көрінетін қозғалыстары басқаша болады. Жоғарғы планета Күн батқаннан кейін батыста көрінеді, жұлдыздар арасымен түзу бойымен қозғалады, яғни Күн сияқты батыстан шығысқа қарай. Бірақ оның қозғалыс жылдамдығы Күннен төмен, Күн планетаны қуып жетеді де планета уақытша көрінбей қалады, себебі ол Күнмен бір мезгілде шығып, бір мезгілде батады. Күн планетадан озады, планета шығыста қайта көрінеді. Планетаның қозғалыс жылдамдығы төмендейді, ол тоқтайды, ал әрі қарай жұлдыздар арасымен кері қарай қозғалады, яғни шығыстан батысқа қарай. Біршама уақыттан соң планета қайта тоқтайды, қозғалыс бағытын түзуге өзгертеді, ал бұл уақытта оны батыс жақтан Күн қайта қуып жетеді, ол тағы да көрінбей қалады, осылайша құбылыстар қайталана береді.

2.1.2. Птолемейдің әлемдік жүйесі

Ежелгі астрономдардың Ғалам туралы түсініктері Птолемейдің "Мегале синтаксис" атты шығармасында баяндалған. Араб ғалымдарының аудармасында ол "Альмагест" деген атпен тараған.

Птолемей жүйесінің негізін төмендегі төрт тұжырым құрайды: 1) Жер Ғалам центрінде орналасқан; 2) Жер қозғалмайды; 3) Барлық аспан денелері жерді айнала қозғалады; 4) Аспан денелері шеңбер бойымен және тұрақты жылдамдықпен қозғалады, яғни бірқалыпты.

Птолемей жасаған әлем жүйесі геоцентрлік деп аталады және оны былайша түсіндіруге болады: планеталар эпицикл деп аталатын дөңгелек бойымен қозғалады, ал өз кезегінде эпициклдардың центрлері деферент деп аталатын басқа дөңгелек бойымен қозғалады, ал олардың жалпы центрінде Жер орналасады. Күн және Ай Жерді айнала деферентер бойымен (эпициклсыз) қозғалады (сурет 2.1).

Аспан шырақтарының тәуліктік қозғалысы тұтастай алғанда бүкіл Ғаламның Жерді айнала қозғалуымен түсіндірілді. Планеталардың тік және кері қозғалыстары былайша түсіндірілді: планета өз эпициклының А нүктесінде тұрған кезде оның Жерден бақыланатын бұрыштық жылдамдығы эпицикл центрінің деферент бойымен және планетаның эпицикл бойымен қозғалыстарының қосындысынан құралады. Бұл жағдайда планета жоғары жылдамдықпен тік қозғалып бара жатқандай қозғалады. Планета В нүктесінде болса, онда оның эпицикл бойымен қозғалысы эпицикл центрінің қозғалысына қарама қарсы бағытта болады және оның жерден бақыланатын бұрыштық жылдамдығы ең аз мәнде болады. Егер эпициклдағы

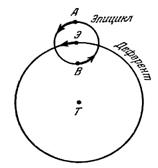
Сурет 2.1. Деферент және эпицикл

планета жылдамдығы эпицикл центрінің жылдамдығынан төмен болса, онда планета бұл жағдайда тік және баяу қозғалып бара жатқандай көрінеді. Егер эпицикл бойындағы жылдамдық эпицикл центрінің жылдамдығынан жоғары болса, онда планета кері қозғалып бара жатқандай көрінеді.

2.1.3. Коперниктің әлемдік жүйесі

Коперник "Аспан сфераларының айналулары туралы"("Об обращений небесных сфер " ) атты кітабында әлем жүйесі туралы көзқарасын баяндаған. Бұл шығармасында Коперник Жер қозғалыстары жөніндегі идеяларын математикалық түрде дәлелдеп, жаңа астрономия дамуына жол бастады. Оның жасаған әлем жүйесі - гелиоцентрлік деп аталды. Бұл жүйенің негізінде келесі тұжырымдар жатыр: 1) Әлем центрінде Күн (гелиос-Күн) орналасқан; 2) Шартәріздес Жер өз осі бойын айнала қозғалады және осы айналыс бүкіл шырақтардың тәуліктік қозғалыстарын түсіндіреді; 3) Жер басқа да планеталар сияқты Күнді айнала қозғалады және осы қозғалыс Күннің жұлдыздар арасындағы көрінетін қозғалысын түсіндіреді; 4) Барлық қозғалыстар бірқалыпты дөңгелектік қозғалыстардың комбинациясы түрінде түсіндіріледі; 5) Планеталардың кері сияқты болып көрінетін қозғалыстары оларға емес, Жерге тән.

Сонымен қатар, Коперник Ай серік ретінде Жерді айнала, ал олар бірге Күнді айнала қозғалады деген пікір айтты. Бақылаулар нәтижесінде Коперник мынадай ойға тоқтады: барлық планеталар (сонымен қатар Жер де) Күнді бір жазықтықта айналып қозғалады. Бірақ бұл жағдайда Жерден көрінетін планеталардың жолдары эклиптика маңайынан орын алады.

Коперник алғаш рет Күн жүйесінің құрылымын дұрыс сипаттап берді. Сонымен қатар, планеталардың Күннен қашықтығын және олардың Күнді айналу периодтарын анықтады. Планеталардың көрінетін қозғалысы Коперник теориясы бойынша өте қарапайым түсіндіріледі.

2.1.4. Планеталардың көрінетін қозғалысы мен конфигурацияларын түсіндіру

Орбиталар бойымен қозғалысы кезінде планеталар Күн және Жерге қатысты түрліше орналасуы мүмкін. Айталық Т Жер өз орбитасында С Күнге қатысты қандай да бір орын алсын.

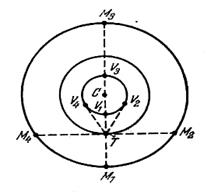
Сурет 2.2. Планеталар конфигурациялары

Төменгі немесе жоғарғы планета бұл уақытта өз орбитасының кез-келген нүктесінде бола алады. Егер V - төменгі планета

суретте көрсетілген V₁,V₂,V₃,V₄ нүктелерінің бірінде орналасса, онда ол Жерден бақылағанда Күнмен төменгі (V₁) немесе жоғарғы (V₃) бірігу нүктелерінен, ең үлкен батыстық (V₂) немесе ең үлкен шығыстық (V₄) элонгация нүктелерінен көрінеді. Егер М - жоғарғы планета М₁,М₂,М₃ және М₄ нүктелерінде орналасса, онда ол Жерден бақылағанда қарсы тұрауы (M₁), бірігіп тұруы (M₃), батыс (M₂) немесе шығыс (M₄) квадраттарда болуы мүмкін. Төменгі планета Жерге төменгі бірігу кезінде ең жақын келеді және жоғарғы бірігу кезінде максималды алшақтайды. (сурет 2.2.).

2.1.5. Планеталар айналуларының синодтық және сидерлік периодтары

Планетаның синодтық айналу периоды (S) деп оның екі бірдей тізбекті кофигурациялар арасындағы уақыт аралығын айтады. Планетаның сидерлік немесе жұлдыздық айналу периоды (T) деп планетаның өз орбитасы бойымен Күнді толық бір рет айналуына кететін уақыт аралығын айтады.

Жердің сидерлік айналу периодын жұлдыздық жыл ( 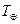) деп атайды. Бұл аталған үш түрлі периодтар арасында қарапайым математикалық тәуелділікті құруға болады. Планетаның тәулік ішіндегі орбита бойымен бұрыштық орын ауыстыруы 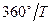, ал Жердікі 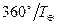. Планета мен Жердің тәуліктік бұрыштық орын ауыстыруларының айырмасы планетаның тәуліктік ығысуына тең, яғни 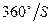. Олай болса төменгі планеталар үшін:

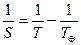(2.1.1)

Жоғарғы планеталар үшін:

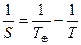(2.1.2)

Бұл теңдеулер синодтық қозғалыс теңдеулері деп аталады.

2.1.6. Кеплер заңдары

Кеплер Коперник ілімін жалғастырушы және дамытушы болды. Бастапқы кезде Кеплер планеталарды шеңбер бойымен қозғалады деп есептеп, кейінірек ол пайымдауларынан бас тартып, планеталар қозғалысының келесі 3 заңын ашты:

1. Барлық планеталар эллипстер бойымен қозғалады және оның бір фокусында Күн тұрады;

2. Планетелардың радиус-векторлары тең уақыт аралықтарында теңдей аудандар сызады;

3. Планеталардың Күнді айналуының сидерлік периодтарының квадраттары олардың эллипстік орбиталарының үлкен жарты осьтерінің кубтарына пропорционал (сурет 2.3).

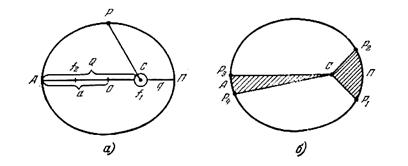
Сурет 2.3. а) Эллипстік орбита; б) Кеплердің екінші заңын түсіндіру

Мұндағы, f₁, f₂ - фокустар, ол АП үлкен оське тең. АО қашықтығы үлкен жартылай ось деп аталады, О-эллипс центрі, Оf₁/OП=е - эллипс эксцентриситеті. Планеталар орбиталарының шеңберден айырмашылығы аз, сондықтан олардың эксцентриситеттері де аз шамаға тең.

2.1.7. Кеплердің 1-ші (жалпылама) заңы

Кеплер өз заңдарын эмпирикалық түрде, планеталардың көрінетін қозғалыстарын зерттеу нәтижесінде алды. Сондықтан жоғарғы келтірілген Кеплердің 1-ші заңы тек Күн жүйесінің үлкен планеталары мен Күнді айналып жүретін олардың денелері үшін дұрыс болады.

Егер аспан денелерінің қозғалысын жалпы түрде қарастырсақ, жоғарғы айтылған заңды келесі түрде тұжырымдау керек: тартылыс күші әсерінен бір дене екінші дененің тарту өрісінде қозғалады, бұл қозғалыс шеңбер, эллипс, парабола немесе гипербола түрінде болады. Бұл тұжырымдамада Кеплердің 1-ші заңы кометалар, үлкен планеталардың серіктері, қос жұлдыздар, т.б. аспан денелері үшін дұрыс болады.

2.1.8. Кеплердің 2-ші заңы

Тік бұрышты координаттар жүйесін қарастырайық. Координаттар басы тартылыс центрінде орналассын, ал ху жазықтығы дене орбитасының жазықтығымен сәйкес болсын. (сурет 2.4)

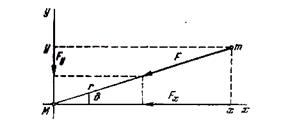
Сурет 2.4 Кеплердің екінші заңын қорытып шығаруға
(М - орталық дене, тартылыс центрі, m – айналатын дене)

Күш пен үдеудің х және у координат осьтеріне құраушыларын тауып, қозғалыс теңдеуін келесі түрде жазайық:

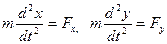(2.1.3)

Бұл теңдеулерді сәйкесінше у және х-ке көбейтіп және алғашқысан соңғысын шегерсек, мынадай өрнекке келеміз:

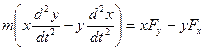(2.1.4)

немесе

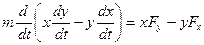(2.1.5)

Күш орталық болғандықтан :

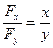, яғни 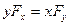(2.1.6)

Олай болса,

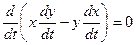(2.1.7) немесе

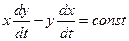(2.1.8)

Полярлы координаттар арқылы өрнектесек:

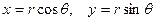, (2.1.9)

мұндағы r - нүктенің координата басынан қашықтығы (радиус-вектор), 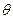- поляр бұрышы. Егер тік бұрышты координаттардан поляр координаттарына көшсек, онда жоғарыдағы өрнек мына түрге келеді:

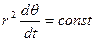(2.1.10)

2.1.9. Кеплердің үшінші (түзетілген) заңы

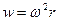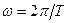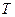Дөңгелектік қозғалыс кезінде үдеу , мұндағы бұрыштық жылдамдық , ал - айналу периоды болса, онда үдеу былайша анықталады:

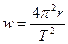(2.1.11)

Массасы m аспан денесінің массасы М орталық денені шеңбер бойымен айнала қозғалысын қарастырайық, олай болса жоғарыдағы өрнекке сәйкес салыстырмалы үдеу мынаған тең:

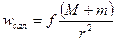, (2.1.12)

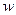және 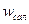– екеуі бір шама, яғни үдеу болғандықтан, теңдеулердің оң жақтарын теңестіріп, келесі өрнекті аламыз:

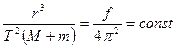(2.1.13)

Аспан дененсінің қозғалысын эллипс бойымен қарастырсақ, сонда (2.1.13) өрнекке ұқсас өрнекті аламыз, бірақ мұнда шеңбер радиусы r үлкен жарты ось а-ға алмастырылады, ал Т дененің эллипс бойымен айналу периодын білдіреді. Осы өрнекті массалары m_ және m₂ екі дене үшін жазайық, олардың эллипстік орбиталарының үлкен жарты осьтері а₁ және а₂, ал айналу периодтарын Т₁ және Т₂ деп белгілесек, сонда:

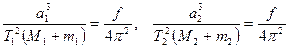(2.1.14)

Бұл Кеплердің 3-ші заңының түзетілген түрі. Егер екі планетаның Күнді айнала қозғалысын қарастырсақ, яғни М₁=М₂ болса және планеталар массасы Күн массасымен салыстырғанда ескермейтіндей аз болса ( 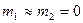), онда Кеплердің бақылаулар нәтижесінде алған өрнегіне келеміз:

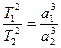(2.1.15)

(2.1.13) және (2.1.14) өнектерінің астрономиядағы маңызы өте зор, өйткені олар аспан денелерінің массаларын аңықтауға мүмкіндік береді.

2.1.10. Ұйытқыған қозғалыс туралы түсінік

Егер Күн жүйесінің қандай да бір денесі Күнге ғана тартылса, онда ол Күн маңайында дәл Кеплер заңдары бойынша қозғалар еді. Бұл екі дене есебінен шешуге сәйкес келетін қозғалыс ұйытқымаған деп аталады. Ал шын мәнінде Күн жүйесіндегі бірде-бір дене дәл эллипс, парабола, гипербола немесе шеңбер бойымен қозғала алмайды. Денелер қозғалысындағы Кеплер заңынан ауытқыған қозғалыс – ұйытқу деп аталады. Ал денелердің шын мәніндегі (реалды) қозғалысы – ұйытқыған қозғалыс деп аталады. Күн және аспан денелерінің ұйытқу сипаты өте күрделі және оларды ескеру өте қиын. Бірақ, ол ұйытқуды шырақтың ұйытқыған және ұйытқымаған кездегі орындарының айырмашылығы ретінде, ал ұйытқыған қозғалысты Кеплердің 3 заңына сәйкес орбитасының элементтері айнымалы деп қарастыруға болады.

Дене орбитасы элементтерініің оның басқа денелермен тартылысы салдарынан өзгеруін – ұйытқу немесе элементтердің теңсіздігі деп аталады. Элементтердің ұйытқуы – ғасырлық және периодты болып бөлінеді.

Ғасырлық ұйытқулар денелер орбиталарының өзара орналасуына тәуелді, ол көп уақыт аралығында соншалықты өзгере қоймайды. Сондықтан элементтердің ғасырлық ұйытқулары бір бағытта жүреді және олардың шамасы уақытқа сәйкес.

Периодты ұйытқулар денелердің өз орбиталарындағы салыстырмалы орнына тәуелді, ол тұйық орбиталар бойымен қозғалады да, қандайда бір уақыт аралығында қайталанып отырады. Сондықтан, орбита элементтерінің периодты ұйытқуларының бағыттары ауысып отырады.

2.1.11. Айдың қозғалыс орбитасы және ұйытқуы

Айдың Жерді айнала ұйытқымаған қозғалыс орбитасы эллипс болып табылады, оның эксцентриситеті 0,055-ке тең, ал үлкен жарты осі 3844400км. Перигейде Жерден Айға дейінгі қашықтық орташадан 21000 км-ге аз, ал Апогейде дәл сондай шамаға көп болады.

Ай орбитасының жазықтығы эклиптика жазықтығына орта есеппен 5°09'-қа көлбеу орналасқан. Ай Жерді айнала батыстан шығысқа қозғалады, яғни Жер Күнді айналған сияқты. Айдың Жерді айналу периоды сидерлік немесе жұлдыздық ай деп аталады. Оның орташа ұзақтығы 27,32 орташа күн тәулігіне тең.

Айдың қозғалысын зерттеу өте қиын, себебі: 1.Ай қозғалысындағы ұйытқулар өте күшті; 2.Ай Жерге жақын, сондықтан қозғалысындағы ауытқулар анық көрінеді, ал оны ескеру керек болады. Ұйытқулар салдарынан Ай орбитасының элементтері үнемі өзгерісте болады. Ай орбитасының барлық элементтері периодты ұйытқуға ұшырайды. Сондықтан Айдың нақты қозғалысы өте күрделі және оны зерттеу аспан механикасының ең қиын есептерінің бірі.