ТАРАУ. Астрофизика элементтері. 3 глава

ол сол ендікте шығып бататын шырақ болады. Бұл шырақтар тәуліктің тең жартысы бойы аспанда болады. Аспан экваторында орналасқан шырақ (d=0) дәл шығыс нүктесінде шығып, батыс нүктесінде батады. Егер d>0 болса шырақ солтүстік шығыста шығып, солтүстік батыста батады, бұл шырақтар тәуліктің жартысынан көп уақыт бойы аспанда болады, ал d<0 болса шырақ оңтүстік шығыста шығып, оңтүстік батыста батады, бұл шырақтар аспанда тәуліктің жартысынан аз уақыт болады. Егер шырақ еңкеюі

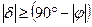(1.5.2)

болса, шырақ батпайтын немесе шықпайтын болады. Батпайтын шырақтың тәуліктік параллелі толығымен горизонт үстінде жатады, олар тәулік бойы аспанда айналып жүреді, ал шықпайтын шырақтың тәуліктік параллелі толығымен горизонт астында жатады, яғни олар бұл ендікте ешқашан көрінбейді.

Экваторда тұрған бақылаушы үшін барлық аспан шырақтары шығып, батады (1.14 сурет). Ал полюстағы бақылаушы үшін барлық көрінетін аспан шырақтары батпайтын шырақтар болады, қалған шырақтар, яғни көрінбейтін шырақтар, шықпайтын шырақтар болады (1.15 сурет). Аспан сферасының шықпайтын және батпайтын шырақтар орналасқан бөліктері бір-біріне тең болады. Көрнекі түрде осы жағдайларды төмендегі суреттен байқауға болады.

Шырақтың аспан меридианын қиып өтуі - шырақ кульминациясы деп аталады. Шырақтың аспан меридианының жоғарғы бөлігін қиып өтуін жоғарғы кульминация, ал төменгі бөлігін қиып өтуін төменгі кульминация деп аталады. Батпайтын шырақтардың екі кульминациясын да бақылауға болады. Шығатын және бататын шырақтардың жоғарғы кульминациясы ғана бақыланады. Шықпайтын шырақтардың екі кульминациясы да бақылауға келмейді.

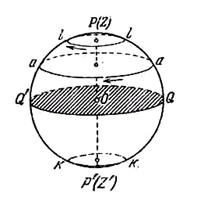
1.15 сурет – Шырақтардың Жердің солтүстік

полюсіндегі тәуліктік қозғалысы

Тәуліктік қозғалыс барысында шырақтардың горизонталды координаттар жүйесіндегі орны тынымсыз өзгеріп отырады. Белгілі бір шырақтың биіктігі немесе зениттік қашықтығы және азимуты уақыт бойынша бірқалыпсыз өзгереді. Кульминация кезінде шырақтың биіктігі немесе зениттік қашықтығы өте баяу өзгереді, ал азимуты өте жылдам өзгереді. Шырақтың шығуы немесе батуы кезінде оның зениттік қашықтығы мен биіктігі былайша: z=90, h=0, ал азимуты шырақтың ауысуы мен бақылау орнының ендігіне байланысты өзгереді және шығу нүктесінің азимуты мен бату нүктесінің азимуты арасында мына қатынас орындалады:

A_ш = -A_б (1.5.3)

Жоғарғы кульминация кезінде шырақтың биіктігі максималды, ал зениттік қашықтығы минималды мәнге ие болады, кульминация нүктесі зениттен оңтүстікке қарай орналасса, азимуты А=0⁰, ал зениттен солтүстікке қарай орналасса, азимуты А=180⁰. Төменгі кульминация кезінде шырақтың биіктігі минимал, ал зениттік қашықтығы максимал мәнге ие болады, кульминация нүктесі зенит немесе надирден оңтүстікке қарай орналасса, азимуты А=0⁰, ал зенит немесе надирден солтүстікке қарай орналасса, азимуты А=180⁰.

Күн, Ай және планеталардан басқа шырақтардың еңкеюі мен тік шарықтауы тәуліктік қозғалыс барысында тұрақты болып қалады, ал сағаттық бұрышы бірқалыпты өзгереді. Сағаттық бұрыштың бірқалыпты өзгеруін уақыт өлшеуде қолданады. Жоғарғы кульминация кезінде шырақтың сағаттық бұрышы t=0, ал төменгі кульминация кезінде t=180⁰.

Берілген ендікте белгілі бір жұлдыз жыл бойы бір нүктеден шығып, сәйкес екінші нүктеде батады. Кульминация нүктелері де өзгеріссіз қалады. Ал Күн, Ай және планеталар үшін шығу, бату және кульминация нүктелері периодты түрде өзгеріп отырады, бұның себебі – бұл денелер Жерге қатысты периодты түрдегі нақты қозғалыста болатынына байланысты, олардың экваторлық координаттарының өзгерісі периодты.

1.6. Параллакстық үшбұрыш және аспан координаттарын өзара түрлендіру

Параллакстық үшбұрыш деп аспан сферасындағы шырақтың вертикал сызығы, сағаттық шеңбері және аспан меридианы доғаларынан құралған үшбұрышты атаймыз (1.11 сурет). Оның төбелері әлем полюсі P, зенит Z және шырақ M болып табылады. Енді осы үшбұрыштың қабырғалары мен бұрыштарын табайық. Егер шырақ аспан сферасының батыс бөлігінде орналасқан болса (1.11 суреттің сол жағы), ZP қабырғасы 90º-j тең (j - бақылау орны ендігі), ZM қабырғасы шырақтың зениттік қашықтығына тең z=90º-h (h - шырақ биіктігі), PM қабырғасы шырақтың полюстік қашықтығына тең p=90º-d (d - шырақ ауысуы). Z төбесіндегі бұрышы 180º-А тең (А - шырақ азимуты), Р төбесінің бұрышы t сағаттық бұрышқа тең, ал М төбесіндегі бұрышы q - параллакстық бұрыш деп аталады. Егер шырақ аспан сферасының шығыс бөлігінде орналасқан болса (1.11 суреттің оң жағы), Р төбесіндегі бұрышы 360º-t тең, Z төбесіндегі бұрышы А-180º тең болады, ал қабырғалары сол күйі қалады.

Тікелей өлшеулер арқылы z (немесе h) пен А анықталады, j - бақылау орны ендігі белгілі десек, шырақтың ауысуын d, сағаттық бұрышын t және тік шарықтауын a=s-t (s-жұлдыздық уақыт) сфералық үшбұрыштарға арналған формулалардан шығарылған мына қатынастар арқылы таба аламыз:

sin d = sin j cos z – cos j sin z cos A,

cos d sin t = sin z sin A, (1.6.1)

cos d cos t = cos j cos z + sin j sin z cos A,

яғни бұл қатынастар горизонталды координаттар жүйесінен экваторлық координаттар жүйесіне өту үшін қолданылады.

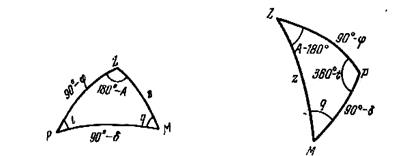
1.16 сурет – Параллакстық үшбұрыш

Егер d, t және j белгілі болып, z және А-ны табу керек болса, онда мына қатынастарды қолданамыз

cos z = sin j sin d + cos j cos d cos t,

sin z sin A = cos d sin t, (1.6.2)

sin z cos A = - cos j sin d + sin j cos d cos t,

яғни бұл қатынастар экваторлық координаттар жүйесінен горизонталды координаттар жүйесіне өту үшін қолданылады. Сонымен қоса жоғарыдағы формулалар шырақтардың шығу және бату уақыттары мен азимуттарын есептеу үшін, бақылау орнының географиялық ендігін және жергілікті жұлдыздық уақытты анықтау үшін қолданылады.

1.7. Қазіргі заманғы астрометрияда координат жүйелерін анықтау

Астрометрияның негізігі міндеті бақылаулар нәтижелеріне сүйене отырып, аспан денелерінің орналасуы мен жылдамдықтарының векторларын және денелер пішінін анықтау. Дененің орналасуы (немесе координаталары) тек басқа бір денеге (немесе таңдап алынған белгілі бір нүктеге) қатысты анықталуы мүмкін. Астрономияда координаттар таңдап алынған санақ жүйесінде анықталады.

Денелердің координаттары мен жылдамдықтарын анықтау үшін классикалық механика қолданылса, санақ жүйесі инерциялық болуға тиісті. Кеңістік Евклидтікі (Ньютон терминологиясы бойынша абсолютті) болып табылады деген болжауда, абсолютті кеңістікке қатысты тыныштықтағы немесе түзусызықты бірқалыпты қозғалыстағы ғана жүйе инерциялық бола алады. Ньютон механикасында уақыт та абсолютті болып табылады, яғни уақыт ағысы сағаттың кеңістіктегі орналасуына және жылдамдығына тәуелсіз болады. Сонда координаттар басын кеңістіктің бір нүктесінен екіншіге ауыстырғанда (яғни бір инерциялық санақ жүйесінен екіншіге ауысқанда) физика заңдары өзгермейді. Олар мұндай координаттар түрлендіруіне қатысты ковариантты болып табылады деп айтады. Бірмезгілде болған екі оқиға арасындағы қашықтық та әр түрлі инерциялық жүйелерде бірдей болады, яғни инвариантты шама болып табылады.

Классикалық механикадан арнайы салыстырмалылық теориясына ауысқанда кейбір ұғымдарды өзгерту керек. Бір инерциялық санақ жүйесінен екіншісіне түрленуі Лоренц теңдеулері көмегімен іске асады. Салыстырмалылық теориясында Лоренц түрлендірулері барысында физика заңдары өзгермейтіні, яғни олар лоренц-ковариантты болып табылатыны дәлелденді. Уақыт өтуі сағаттың кеңістіктегі жылдамдығына тәуелді болады. Бұл әртүрлі инерциялық жүйелердегі екі оқиға арасындағы уақыт аралығы инвариант болып табылмайтынын көрсетеді: мысалы, меншікті уақыт (яғни қозғалыстағы бақылаушымен байланыстырылған лабораториялық санақ жүйесінде өлшенетін уақыт) инерциялық координаттар жүйесіне қатысты тыныштықтағы сағатпен өлшенетін уақыттан баяу өтеді.

Тартылыс өрістері болғанда салыстырмалылықтың арнайы теориясының заңдары жалпы жағдайда орындалмайды. Бірақ, салыстырмалылықтың жалпы теориясы көрсететіндей, кеңістіктің шектелген аймақтарында арнайы тәсіл көмегімен үдемелі қозғалатын кооринаттар жүйесін таңдап алуға болады: жүйенің үдеуі кеңістіктің қарастырылып отырған аймағына орналастырылған еркін бөлшек алатын үдеуіне (яғни бұл аймақтағы гравитациялық өрістің әсерінен алатын удеуіне) тең болса, онда бұл жуйені локальды инерциялық деп есептеуге болады. Бұл жүйеде салыстырмалылықтың арнайы теориясының заңдары жоғары дәлдікпен орындалады. Бір локальды инерциялық жүйеден екіншісіне ауысқан кезде координаттар түрлендіруі Лоренц теңдеулерімен анықталады.

Санақ жүйесі теориялық ұғым болып табылатыны түсінікті: сол жүйенің негізгі жазықтықтар мен нүктелер, сондай-ақ координат остері ресми келісімдер негізінде белгіленеді. Астрономияда колданылатын негізгі жүйелер туралы жоғарыда айтылды.

Ал аспанда (аспан сферасында) бұл нүктелер мен осьтер белгілінген (сызылған) емес. Сондықтан астрономияда координаттар жүйелерін анықтау (белгілеу) үшін аспан денелері қолданылады. Яғни, санақ жүйесінің жүзеге асырылуы (практикадағы реализациясы) ретінде қалап алынған белгілі бір сандағы объектілердің (мысалы, жұлдыздардың немесе радиокөздердің) координаттары мен жылдамдықтарының тізімі қабылданады. Мұндай тізім каталог деп аталады. Әр жеке каталог санақ жүйенің жүзеге асырылуларының (реализацияларының) бірі болып табылады.

Іс жүзінде санақ жүйесінің негізгі жазықтықтар мен осьтерін екі тәсіл көмегімен анықтауға болады: кинематикалық және динамикалық. Кинематикалық тәсілдің мағынасы мынада: егер координаттары белгілі және тұрақты болып қалатын денелер бар болса, онда бұл денелермен инерциялық немесе астрометрияда қабылданғандай, іргелі (түбегейлі, фундаменталды) координаттар жүйесін байланыстыруғы болады.

Бірақ бақылаулар кезінде қателіктер болуы себепті, іс жүзінде аспан денелерінің координаттары дәлме-дәл белгілі болмайды, олар әртүрлі себептер салдарынан өзгеруі мүмкін. Бұл жағдайда инерциялық жүйеге ең жақын жуықтау ретінде координаттары ең жоғары дәлдікпен белгілі және тек кездейсоқ қателіктерден бұрмаланған объектілермен анықталатын жүйе алынады. Мұндай жүйе орта есеппен алғандаайналмайды деп санап, оны квазиинерциялық деп есептеуге болады. Қазіргі уақытта Галактикадан тыс радиокөздердің координаттарымен белгіленетін жүйе ең жақсы жүйе болып табылады. Жұлдыздардың HIPPARCOS каталогы квазиинерциялық жүйенің ең жақсы оптикалық жүзеге асырылуы болып табылады.

HIPPARCOS ғарыштық жобасы 20 ғ. 90-шы жылдары іске асырылған еді, оның негізгі жетістіктерінің бірі – Күннен 1 кпк-ке дейінгі қашықтықта орналасқан 120000-ға жуық жұлдыздардың параллакстарын (демек оларға дейінгі қашықтықтарды) жоғары дәлдікпен өлшеу (олардың дәлдігі жоғары каталогын жасау). Бұл жұлдыздар орналасқан көлем Галактика көлемінің өте аз бөлігі болып табылса да, аталған қашықтықтарды анықтау өте маңызды іс болып табылады, өйткені ол Күннің ең жақын төнірегінің үшөлшемді суретін құруға мүмкіндік берді.

Егер санақ денелері ретінде Күн жүйесінің құрамына кіретін денелер алынса және олардың координаттары Кориолис мүшелері енгізілмеген қозғалыс теңдеулері негізінде анықталса, онда координаттар жүйесі динамикалық тәсіл көмегімен анықталған деп аталады. Ең қарапайым жағдайда, яғни дене орталық денеге қатысты эллипстік орбита бойымен Кеплер қозғалысында болған кезде, координаттар жүйесін орбита жазықтығымен анықтауға болады (бұл жағдайда орбита өзінің кеңістіктегі орналасуын сақтайды); z осін орбита жазықтығына перпендикуляр деп белгілеуге, ал x осі ретінде эллипстің үлкен жартыосін алуға болады. Ньютон механикасы шеңберінде х осі өзінің орбита жазықтығындағы орналасуын сақтайды. y осін арнайы теңдеумен анықтап беріп, координаттардың инерциялық жүйесін анықтауға болады. Дененің айналу периоды тұрақты болғандықтан, динамикалық санақ жүйесінде уақыттың динамикалық шкаласын анықтауға болады, оны эфемеридалық деп атайды.

Іс жүзінде орбита жазықтығының кеңістіктегі орналасуы да, үлкен жартыосьтің орбита жазықтығындағы орналасуы да күн жүйесінің басқа денелерінің әсерінен пайда болатын ұйытқулар және салыстырмалылықтың жалпы теориясының эффектілері себебінен тұрақты болып қалмайды. Сондықтан динамикалық санақ жүйесі эфемеридалармен, яғни Күн, Ай және үлкен планеталардың орналасулары кестелерімен беріледі. Қазіргі уақытта Реактивті қозғалыс лабораториясымен (Jet Propulsion Laboratory, JPI) есептелген DE200/LE200, DE403/LE403 және DE405/LE405 эфемеридалар кең қолданылады. DE405/LE405 эфемеридалар Жер айналуының халықаралық қызметімен (International Earth Rotation Service, IERS) стандарт ретінде қолдану үшін ұсынылған және олар жуырда жылнамаларды құрастыру үшін негіз болып табылатын DE200/LE200 эфемеридаларды алмастырады деп күтілуде.

Динамикалық эклиптиканың кинематикалық жүйедегі орналасуын анықтау үшін арнайы зерттеулер (Айдың қозғалысын зерттеу, ғарыштық зондтардың квазарларға қатысты бақылаулары, яғни бірмезгілде кинематикалық та, динамикалық та жүйелердегі бақылаулар, т.с.с.) қажет. Көктемгі күн мен түннің теңелу нүктесін кинематикалық жүйеге байланыстырудың ең ұтымды әдісі - асаұзын базалардағы радиоинтерферометрлер (АҰБР, олар туралы сөз кейінірек болады) көмегімен пульсарларды квазарларға қатысты бақылау және онымен бірмезгілде пульсарларды хронометрлеу (немесе тайминг).

1.8. Каталог дәуірі, стандарт дәуірі, күн мен түннің теңелу дәуірі

Жоғарыда бірнеше рет дәуір деген термин қолданылды. Бақылаушы өлшейтін уақыттың әртүрлі мезеттерінде аспан денелерінің координаттары прецессия, нутация (яғни Жердің айналу өсінің кеңістіктегі орналасуының өзгеруі, бұл құбылыстар туралы кейін сөз болады), тағы басқа себептерден өзгереді.

Мысалы, прецессия нәтижесінде аспан экваторының жазықтығы кеңістіктегі орналасуын сақтамайды, әлем полюстері 26000 жыл ішінде аспан сферасында шеңберлерді сызады. Шамамен 4500 жыл бұрын әлемнің солтюстік полюсі Айдаһардың α жұлдызы (Тубан) қасында орналасты, бұл жұлдыз сол кезде полюстік болды. 2000 жылдан кейін полюстік жұлдыз Цефейдің g-сы (Альран), ал 14000 жылдан кейін Лира шоқжұлдыздың Вега жұлдызы болады. Егер аспан экваторының белгілі бір уақыт мезетіндегі орналасуын есептеген кезде тек прецессия еске алынса, ал нутация ескерілмесе, онда мұндай экватор орта экватор деп аталады.

Прецессия себебінен күн мен түннің теңелу нүктелері де ығысатыны түсінікті: қазіргі уақытта көктемгі күн мен түннің теңелу нүктесі Балықтар шоқжұлдызында, күзгі күн мен түннің теңелу нүктесі – Бикеш шоқжұлдызында орналасқан, ал біздің дәуір басында олар Тоқты мен Таразы шоқжұлдыздарда орналасқан, мұнымен бұл нүктелердің қолданатын белгілеулері байланысты (^ және d - Тоқты мен Таразының белгілеулері).

Шырақтар координаттарының өзгеруін есептеу үшін ең алдымен бақылаулар арасындағы уақыт аралығын өлшеу керек.

Уақытты өлшеу үшін кейбір периодты процесс таңдап алынады. Екі оқиға арасындағы аралықтың ұзақтығын өлшеу бұл аралықты таңдап алынған процестің периодымен салыстыруда тұрады. Сонымен, бір жағынан, бақылауды жүргізудің мезетін, яғни бақылау дәуірін, максимал дәлдікпен анықтау керек, екінші жағынан, екі дәуір арасындағы интервалды уақыт шкаласының таңдап алынған бірліктер түрінде өлшеу қажет. Баяғы заманнан уақытты санаудын негізгі бірліктері ретінде Жердің өз осі бойымен және Күн бойымен айналуының периодын көрсететін тәулік пен жыл алынады. Бақылау дәлдігі өсуі мен Жер айналуының бірқалыпсыздығының ашылуымен байланысты, қазір дәлдігі жоғарылау уақыт шкалалары енгізілген. Оларды кейін толығырақ қарастырамыз.

Каталогты құрастырған кезде әр жұлдыз бір немесе бірнеше жыл бойында бірнеше рет бақыланады. Мұның нәтижесінде әр мезет, не бақылау дәуірі үшін жұлдыздардың көрінетін координаттары анықталады. Каталог дәуірі деп каталог жұлдыздарын бақылаудың орташа дәуірін айтады. ХАО (халықаралық астрономиялық орталық) жұлдыздар мен радиокөздер координаталарын стандарт дәуірлер деп аталатын таңдап алынған уақыт мезеттері үшін анықталған орта экваторға қатыстыруды ұсынады. Былайша айтсақ, жұлдыздар координаттарын салыстыру мақсатында оларды стандарт дәуір үшін белгіленген бірыңғай координаттар жүйесіне келтіру қажет. Қазіргі уақытта стандарт дәуір ретінде J2000.0 (яғни 2000 жылдың 15-ші қаңтары алынады, 1 қосымшаны қараңыз). Уақыт мезеті геоцентрлік жүйе үшін жер уақыт шкаласында анықталады (Terrestеrial Time, TT).

Күн мен түн теңелуінің дәуірі деп аспан экваторы мен эклиптиканың сәйкес орналасуы, демек күн мен түннің теңелу нүктесі бекітілетін дәуірді айтады. Мысалы, HIPPARCOS каталогының дәуірі - J1991.25 дәуір. Бұл каталогта жұлдыздар координаттары J1991.25 мезеті үшін, ал экватор жазықтығының кеңістіктегі орналасуы - J2000.0 мезеті үшін берілген.

Салыстырмалылықтың жалпы теориясында уақыт ағысы тек қана сағаттың жылдамдығына емес, оған қоса сағаттың орналасуына да, дәлірек айтсақ, сағат орналасқан жердегі гравитациялық өрісті сипаттайтын және гравитациялық потенциал деп аталатын функцияға тәуелді болады. Сондықтан қалап алынған санақ жүйесінде «координаттық» уақыт енгізіледі де, бір жүйеден екіншіге өтудегі уақыттың түрлендіру заңы, яғни басқа координаттық немесе меншікті (егер санақ жүйесі бақылаушамен байланысты болса) уақытқа ауысу заңы, анықталады. Бақылауларды өңдеген кезде бақылау дәуірі, не каталог дәуірі таңдап алынған санақ жүйесімен байланыстырылған уақыт шкаласында беріледі.

1.9. Қазіргі заманғы астрометрияда координат жүйелерін жүзеге асыру

Енді координаттардың аспан жүйелерінің әртүрлі жүзеге асыруларын толығырақ қарастырайық.

1998 жылға дейін квазиинерциялық жүйе 1535 жұлдызды кіргізетін FK5 (фундаменталь каталог 5) түрінде жүзеге асырылған еді. Бұл жұлдыздардың координаттары бір жылда ~0’’,08 қателікпен, ал меншікті қозғалыстар доғаның ~1 мс қателікпен белгілі. Қосымша каталог (FK5-sup.) 3117 жұлдызды кіргізеді, олардың координаттары мен меншікті қозғалыстары көбірек қателіктермен белгілі: бір жылда ~0’’,12 және доғаның 2 мс-і, сәйкесінше. FK5 жүйенің негізгі жазықтығы J2000.0 стандарт дәуіріндегі экватормен, ал тік шарықтауларды санау басы – экватордың эклиптикамен J2000.0 дәуіріндегі қиылысуымен, дәлірек айтсақ сол дәуірде Күн центрі аспан экваторын оңтүстік жартышардан солтүстік жартышарға қозғалған кезде қиып өту нүктесімен (^ нүктемен) анықталған еді. Жер мен Күннің координаттары, демек эклиптиканың орналасуы, күн жүйесінің денелерін бақылау және олар үшін динамика теңдеулерін шешу негізінде (яғни динамикалық әдіспен) анықталған. Сондықтан экватор мен эклиптиканың қиылысуымен анықталатын күн мен түннің теңелу нүктелері динамикалық күн мен түннің теңелу нүктелері деп, ал Күн центрінің көктемгі күн мен түн теңелуінің динамикалық нүктесі арқылы өту мезеті – динамикалық күн мен түннің теңелуі деп аталады. Демек FK5 жүйедегі тік шарықтаулардың санау басы динамикалық күн мен түннің теңелу нүктесі болып табылады да, ^_J2000.0 деп белгіленеді.

Бірақ АҰБР-ғы бақылаулар нутацияның ХАО1980 теориясында болған қателіктер себебінен J2000.0 дәуіріндегі орташа аспан экваторы FK5 жүйесінің экваторымен беттеспейтінін, сондықтан J2000.0 экваторға сәйкес келетін P_J2000.0 полюсі де P_FK5 полюстерге қатысты ығысқан екендігн көрсетті. Осыған сәйкес, FK5 жүйесіндегі тік шарықтауларды есептеу басы (О_FK5) де ^_J2000.0 нүктемен беттеспейді.

1998 ж. 1 қантарынан бастап ХАО шешімі бойынша аспан координаттар жүйесі ретінде галактикадан тыс радиокөздер каталогы қабылданған, ол Координаттардың халықаралық аспан жүйесі (International Celesterial Reference System - ICRS) деп аталады. ICRS 212 тірек радиокөздердің координаттарымен жүзеге асырылады. Тығыздау толтырылу үшін оларға координаттары аз дәлдікпен өлшенген 396 қосымша көздер қосылған. Жаңа санақ жүйесінің жасалуы АҰБР –дағы 20-жылдық бақылаулар нәтижелерінің арқасында мүмкін болды. ICRS - ң остері квазарларға қатысты бекітілген.

Жаңа санақ жүйесі кинематикалық принципте негізделген: жүйенің остері Әлемнің белгілі объектер ішіндегі ең алшақтарына қатысты қозғалмайтын болып қалады. ХАО ұсынысына сәйкес ICRS жүйенің полюсі FK5 полюсімен оның қателіктері шегінде ( 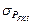=доғаның 50 мс) келіседі және J2000.0 полюсіне жақын болып табылады (1.12 сурет). ICRS жүйенің тік шарықтауларды есептеу басы да FK5 жүйемен келісілген және J2000.0 динамикалық күн мен түннің теңелуіне жақын. Яғни ХАО ұсынысы бойынша ICRS остерінің бағыттары FK5 жүйемен келісілген.