ТАРАУ. Астрофизика элементтері. 1 глава
Тарау
Сфералық астрономия негіздері
Сфералық астрономия - математикалық әдістер негізінде сфералық аспан координаттар жүйелерін анықтау, аспан денелерінің координаттарын бір жүйеден басқаға түрлендіру формулаларын шығару, уақытты өлшеу шкалаларын анықтау және олардың арасындағы байланысты тағайындау, астрономиялық бақылау нәтижелерін редукциялау мәселелерімен айналысатын бөлім.
Сфералық астрономия астрометриямен өте тығыз байланысты. Астрометрия - аспан денелерінің орны мен қозғалысын, Жердің айналуын және аспан денелері мен Жердің пішінін зерттеп білумен, сондай-ақ уақытты анықтау және сақтаумен айналысатын астрономияның бөлімі. Бұл мәселелерді астрометрия аспандағы бұрыштарды өлшеудің теориялық және техникалық әдістеріне сүйеніп шешеді. Дәлірек айтсақ, астрометрия аспан координаттары жүйелерін жүзеге асыру, аспан денелерінің координаттарын өлшеу, Жердің айналуын мейлінше толық сипаттайтын параметрлер жиынын табу, астрономиялық бақылаулар негізінде дәл уақытты анықтау (уақыт қызметі), күнтізбе құру, жер бетіндегі нүктелердің географиялық координаттарын бақылаулар көмегімен дәл анықтау сияқты мәселелермен, сондай-ақ бұл мәселелерді шешудің теориялық және практикалық әдістерін табу және әрі қарай жетілдірумен айналысады.
Сфералық астрономия мен астрометрияның айырмашылығын былайша көрсетуге болады. Сфералық астрономияның негізгі міндеттерінің бірі аспан координаттар жүйелерін теориялық түрде анықтау (жүйенің негізгі жазықтықтары мен нүктелерін, координат осьтерін ресми келісімдер негізінде тағайындау) болса, астрометрия бұл жүйелерді каталогтар деп аталатын жұлдыздар, радиокөздер, басқа да аспан объектілерінің координаттары мен жылдамдықтарының тізімдері түрінде жүзеге асырады (аспан координаттары жүйелерін жүзеге тек осылай асыруға болатындығын аспанда координаттар жүйелерінің нүктелері мен осьтері белгіленбеуімен (сызылмаған) түсіндіруге болады).
Астрометрия астрономиялық құрылғыларды жасау мен бақылаулар әдістерін жасаумен айналысатын практикалық астрономия бағытымен де тығыз байланысты. Жалпы, астрономияның аталған бөлімдері мен астрометрияның арасында анық шекара жоқ болғандықтан, сфералық астрономия мен практикалық астрономияны астрометрияның екі негізгі бөлігі ретінде де қарастыруға болады.
1.1. Аспан. Аспан денелерінің көрінетін қозғалыстары
Жер бетінің кез-келген нүктесінен бақылаушы аспанды сфералық бет (жартысфера) ретінде көреді. Ауа райы бұлтсыз болған жағдайда аспанның түсі күндіз көгілдір болады және онда біз жалғыз аспан шырағы ретінде Күнді, кей кезде онымен қоса Айды көре аламыз; ал түнде болса көптеген аспан шырақтарын байқай аламыз. Түнде көрінетін аспан шырақтарының көбі жұлдыздар. Аспан шырақтарының көптігі санауға келмейтін сияқты болғанымен, олардың көзге көрінетіндерінің жалпы саны 6 мыңдай, ал бақылаушыға нақты мезетте көрінетіндерінің саны 3 мыңдай.
Аспандағы жұлдыздардың өзара орналасуы өте баяу өзгереді. Бұл өзгеріс мыңдаған жылдар өткенде әзер байқалады. Сондықтан олардың ішінде жарық жұлдыздарды ерекшелеп, топтарға бөліп, ажыратуға болады. Жұлдыздарды шоғырларға бөлу ежелден қалыптасқан. Көбінесе олар жануарлар мен аты аңызға айналған кейіпкерлердің атымен, кейде ұқсас пішінді заттың атымен аталған. Жалпы, әр халық жұлдыздарды өзінше топтастырып, атаулар берген. Кейбір жарық жұлдыздарға да жеке атаулар берілген. Б.з.д. 3 ғ. грек астрономдары шоқжұлдыздар атауын бір жүйеге келтіріп, кейін 8 ғ. бастап араптар, олардан соң 17 ғ. бастап сәйкес атауларды европа астрономдары қолдана бастады. Қазіргі уақытта жұлдыздар шоғыры мен жарық жұлдыздар атауында грекше, латынша, арапша және қазіргі заманғы атаулар кездеседі. 17 ғ. бастап шоқжұлдыздар құрамындағы жұлдыздар грек әріптерімен белгілене бастады. Кейінірек, бақылау құралдарының дамуына байланысты жарқырауы әлсіз жұлыздарды көптеп тіркей бастаған соң оларды сандармен белгілеу енгізілді. 130-ға жуық жарық жұлдыздарға жеке атаулар берілді (мысалы, Орион шоқжұлдызының α жұлдызы – Бетельгейзе, β жұлдызы - Ригель). 1919 ж. құрылған Халықаралық астрономиялық одақтың 1922 жылғы I құрылтайында шоқжұлдыздар шекарасы қайта қаралып, кейбір ірі шоқжұлдыздар бірнешеге бөлінді, ал шоқжұлдыздар деп жарық жұлдыздар тобын емес, аспанның белгілі бір бөлігін қарастыратын болып келісті. Қазір бүкіл аспан шартты түрде 88 шоқжұлдызға бөлінген.
Ашық түнде жұлдызды аспанды бірнеше сағат бойы бақыласақ, аспан тұтастай, ондағы шырақтармен бірге бақылау жер арқылы өтетін ойша сызылған қандай да бір ось бойымен шығыстан батысқа қарай үздіксіз айналыста болатынын байқай аламыз. Жердің өз өсі бойымен батыстан шығысқа қарай айналуынан болатын аспан мен шырақтардың бұл көрінетін қозғалысын тәуліктік қозғалыс деп атайды (Жердің өз өсі бойымен айналу периоды бір тәуілікке тең болғандықтан, аспан да бір толық айналымды бір тәулік ішінде жасап бітіреді). Біраз уақыт бақылап отырған бақылаушы шырақтардың көп бөлігі шығыс жақтан шығып, батыс жақта бататынын, ал кейбір шырақтар батпастан белгілі бір нүктені айнала қозғалатынын байқайды. Солтүстік жартышардағы мұндай нүкте әлемнің солтүстік полюсі деп аталады, оңтүстік жартышардағы мұндай нүкте әлемнің оңтүстік полюсі болып табылады. Қазақстан солтүстік жартышарда болғандықтан, осындағы бақылаушы аспан Темірқазық жұлдызына жақын орналасқан әлемнің солтүстік полюсін сағат тіліне қарама-қарсы бағытта айнала қозғалатынын байқайды.
Ал егер Күн мен Айды күнделікті мұқият бақыласақ, олар жұлдыздарға қатысты 12 шоқжұлдыз арқылы өтетін бір сызық бойымен тәуліктік қозғалыс бағытына қарама-қарсы бағытта қозғалатынын және жұлдыздарға қарағандағы өз орындарына белгілі бір жиілікпен қайталап келетінін (Күн 365,24 тәулікте, Ай 27,32 тәулікте) байқаймыз. Күн мен Ай сияқты кейбір аспан шырақтары да өздерінің жұлдыздарға қатысты орнын 12 шоқжұлдыз бойында өзгертетінін астрономдар ежелден байқаған. Оларды жұлдыздардан ерекшелеп “планеталар” (қалықтаған шырақтар) деп атаған. Ол кезде тек 5 планета белгілі болған: Юпитер, Сатурн, Шолпан, Марс, Меркурий. 18-20 ғ.ғ. аралығында қалған үш планета (Уран – 1781 ж., Нептун – 1846 ж., Плутон – 1930 ж.) ашылды. Планеталардың көрінетін қозғалысы кейде күннің қозғалыс бағытымен бағыттас, кейде кері бағытта болады. Ал жоғарыда айтылған 12 шоқжұлдызды зодиактық (грекше “зоон” – жануар сөзінен шыққан) шоқжұлдыздар деп атайды. Олар Балықтар, Тоқты, Торпақ, Егіздер, Шаян, Арыстан, Бикеш, Таразы, Сарышаян, Мерген, Ешкімүйіз және Суқұйғыш шоқжұлдыздары. Күн олардың бірінші үштігін көктемде, екінші үштігін жазда, үшінші үштігін күзде, қалған үшеуін қыста басып өтеді. Жалпы әр зодиактық шоқжұлдызды Күн бір айдай уақытта басып өтеді.
1.2. Сфералық геометрияның негізгі ұғымдары. Сфералық үшбұрыштар
Астрономияның көптеген мәселелерін шешу үшін аспандағы шырақтарға дейінгі қашықтықты анықтаудың қажеті жоқ. Астрометриялық өлшеулер үшін аспандағы шырақтардың көрінетін орнын оларға дейінгі бағытпен сипаттап, өзара орналасуын сол бағыттар арасындағы бұрыштармен анықтау жеткілікті. Мұндай өлшеулер жасауда аспанды белгілі бір сфера, ал аспандағы шырақтарды сол сфера бетінде орналасқан деп қарастырған ыңғайлы. Бұл сфераны аспан сферасы деп атайды, оның радиусын кез-келген деп алуға болады, бірақ есептеулерді жүргізу үшін оны 1 тең деп алуға ыңғайлы.
Осыдан астрометрияның көптеген мәселелерін шешу сфералық геометрияның әдістерімен жұмыс істеуге келіп тірелетіні түсінікті: аспан сферасы стереометрияда қарастырылатын сфераның барлық қасиеттеріне ие. Осылардың бізге қажетті болатын кейбіреулерін атап өтейік.
Сфераның ортасынан (центрінен) өтетін жазықтықтың сферамен қиылысу сызығы радиусы сфераның радиусына тең үлкен шеңбер болып табылады (1.1 сурет). Бұл шеңбермен шектелген осы жазықтықтың бөлігі үлкен дөңгелек деп аталады. Ол сфераны екі жартысфераға бөледі. Екі үлкен шеңбер диаметралды қарама-қарсы екі нүктеде қиылысады.
Сфера бетінде жатқан кез-келген екі нүкте арқылы үлкен шеңберді өткізуге болады (бұл тоқтам планиметрияның екі кез-келген нүкте арқылы түзуді жүргізуге болады деген аксиомасына баламалы). Аспан сферасының кез-келген екі нүктесі арасындағы қашықтықты сәйкес орталық радиус- векторлар арасындағы бұрышпен немесе осы екі нүкте арқылы өтетін үлкен шеңбер доғасымен өлшеуге болады. (Сфералық геометрияда бұл доға планиметриядағы түзудің орнына екі нүктені қосатын ұзындығы ең аз сызық болып табылады).
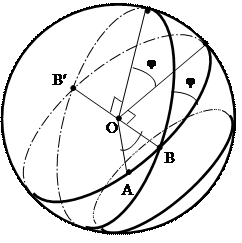 |
1.1 сурет – Сфералық геометрияның негізгі ұғымдары.
Аспан сферасын оның ортасынан өтпейтін жазықтықпен қиғанда кіші шеңбер шығады.
Сфералық үшбұрыш деп сфера бетіндегі үш үлкен шеңберлер доғаларынан құралған пішінді айтамыз (1.2 сурет). Сфералық үшбұрыштың бұрыштары ретінде оны құрайтын үлкен шеңберлердің жазықтықтары арасындағы бұрыштарды (мұндай бұрыштарды екіқырлы (екіжақты) деп атайды, 1.1 суреттегі j бұрышы) алады. Біз қарастыратын жағдайларда бұл бұрыштардың әр қайсысы 180º аспайды, ал үшбұрыш бұрыштарының қосындысы сәйкесінше 540º аспайды, бірақ 180º кем болмайды. Сфералық артық бұрыш s деп үшбұрыш бұрыштарының қосындысынан 180º алып тастағанда шығатын шаманы айтамыз:
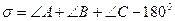 (1.2.1)
(1.2.1)
Сфералық үшбұрыштың ауданы
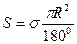 , (1.2.2)
, (1.2.2)
мұндағы R – сфера радиусы.
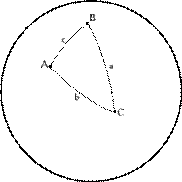
1.2 сурет - Сфералық үшбұрыш
Сфералық үшбұрыштардың қабырғалары үлкен шеңберлердің доғалары болғандықтан, оларды сол үшбұрыштардың бұрыштары тәрізді градустармен өлшеу қабылданған. Яғни сфералық үшбұрыштың қабырғасы болып табылатын доға ұзындығы оның ұштарын сфера центрімен (ортасымен) қосатын екі радиус-вектордың арасындағы бұрышпен өлшенеді. Сфералық үшбұрыштардың A бұрышына қарама-қарсы жатқан қабырғасын (доғасын) a деп, B бұрышына қарама-қарсы жатқан қабырғасын (доғасын) b деп, C бұрышына қарама-қарсы жатқан қабырғасын (доғасын) c деп белгілейік. Сонда сфералық үшбұрыштар үшін мына формулалар орындалады [1]:
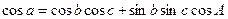 (1.2.3)
(1.2.3)
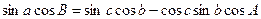 (1.2.4)
(1.2.4)
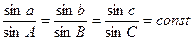 , (1.2.5)
, (1.2.5)
мұндағы (1.2.3) формула косинустар формуласы, (1.2.4) формула бес элементтер формуласы, ал үшінші формула синустар формуласы деп аталады. Осы үш қатынас сфералық үшбұрыштар мәселесін шешуде негізгі роль атқарады. Сфералық үшбұрыштың бір бұрышы тік болса, мысалы А=90º, жоғарғы қатынастардан мына формула шығаруға болады
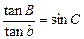 . (1.2.6)
. (1.2.6)
1.3. Жер пішіні. Географиялық координаттар
Астрономиялық бақылаулардың басым көпшілігі Жер бетінен жүргізілетіндіктен, бақылаушының қай жерде тұрғанына тәуелді болады. Бақылаушының орның анықтау үшін қажет болатын негізгі географиялық түсніктер мен терминдер және Жер пішіні туралы мәліметті шолып өтейік.
Жер пішінін бірінші жуықтауда радиусы R)=6370 км болатын шар деп қарастырсақ болады. Жер өзінің масса центрінен өтетін белгілі бір ойша алынған түзу (PNPS) бойымен айналады, оны Жердің айналу осі деп атайды. Осы остің жер бетін қиып өтетін нүктелері солтүстік (PN) және оңтүстік (PS) географиялық полюстер деп аталады. Солтүстік полюске сырттан қарағанда Жер сағат тіліне қарсы бағытта айналады.
Айналу осіне перпендикуляр жазықтықта орналасқан Жер бетіндегі үлкен шеңбер Жер экваторы деп аталады. Осы сызық Жер бетін солтүстік және оңтүстік жартышарларға бөледі. Жер экваторына паралель кіші шеңберлер географиялық паралельдер деп аталады. Екі полюсты қосатын үлкен жартышеңберлер географиялық меридиандар деп аталады. Гринвич обсерваториясы арқылы өтетін географиялық меридианды бас меридиан деп атайды. Бас меридиан жатқан жазықтық Жер бетін батыс және шығыс жартышарларға бөледі.
Жердің берілген нүктедегі ауырлық күшінің бағытымен бағыттас түзу сызық ілме немесе вертикаль (тік) сызық деп аталады.
Жер бетіндегі кез келген нүкте екі географиялық координатпен толық анықталады. Олардың бірі – φ, географиялық ендік, екіншісі – λ, географиялық бойлық.
Берілген О нүктесінің географиялық ендігі деп сол нүктедегі ілменің Жер экваторы жазықтығымен жасайтын бұрышын айтамыз. Географиялық ендік экватордан бастап солтүстік полюске дейн 0○ пен +90○ (солтүстік ендік) аралығында, ал оңтүстік полюске дейін 0○ пен -90○ (оңтүстік ендік) аралығында өзгереді.
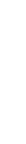
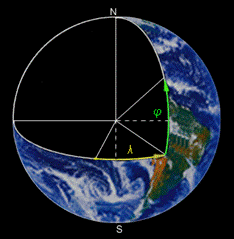
1.3 сурет – Географиялық координаттарды анықтау
Берілген О нүктесінің географиялық бойлығы деп сол нүктеден өтетін географиялық меридиан жатқан жазықтық пен бас меридиан жатқан жазықтықтық арасындағы екіжақтық бұрышты айтамыз (1.3 сурет). Географиялық бойлық бас меридианнан бастап шығысқа қарай (яғни Жердің айналу бағытында) градустармен өлшегенде 0○ пен 360○ немесе, сағатпен өлшегенде, 0h ÷ 24h аралығында өзгереді. Географияда бойлықты шығысқа қарай 0○ ÷ +180○ (шығыс бойлық) аралығында, батысқа қарай 0○ ÷ -180○ (батыс бойлық) аралығында өлшейді.
Жоғарыда айтылғандай, көптеген астрономиялық есептерді шешу кезінде Жерді радиусы 6370 км тең біртекті шар ретінде қарастыруға болады. Бұл жағдайда кез келген нүктедегі ілме сызығы Жер центрінен өтеді, ал географиялық меридиандар мен экватор радиустары бірдей (Жер радиусына тең) шеңберлер болып табылады деп есептеуге болады. Онда Жердің кейбір нүктесінің географиялық ендігін меридианның экватордан бұл нүктеге дейінгі доғасымен, ал географиялық бойлығын экватордың бас меридианнан осы нүктеден өтетін меридианға дейінгі доғасымен өлшеуге болады.
Бірақ жоғары дәлдікті қажет ететін өлшеулер үшін Жерді шар деп қарастыруға болмайды, өйткені ол өз осінен айналғандықтан, Жер затына әсер арқылы центрден тепкіш инерциялық күш пайда болады да, бұл әсерден Жер айналу осі бойымен сығылған болады. Оған қоса Жер беті нүктелерінің биіктігі континенттер шегінде бірнеше километр аралықта өзгереді. Сондықтан Жердің дәл пішіні ешбір белгілі математикалық фигураға сәйкес келмейді. Ыңғайлылық үшін Жердің нақты күрделі физикалық бетін қарапайым математикалық пішінмен жуықтау керек. Жер бетін жуықтайтын фигуралар ретінде геоид пен айналма эллипсоидты алады.
Жалпы, Жер пішіні ретінде Жер қыртысындағы қатпарлар мен ойпаттарды елемегендегі геоидты қабылдауға болады. Геоид деп Жер бетін түгелдей су басып жатыр және толқындар мен Жерге басқа аспан денелері тарапынан әсер ететін тасу күштері жоқ деп жорамалдаған жағдайдағы беттің қабылдайтын пішінін айтады. Мұндай бет жердің тепе-теңдік (деңгейлік, эквипотенциялық) беттерінің біріне сәйкес келеді. Тепе-теңдік бет деп кез-келген нүктеде ілме сызығына нормаль болып табылатын бетті атаймыз. Сонымен, геоид – бұл орташа теңіз деңгейіне сәйкес келетін, барлық нүктелері ауырлық күшіне нормаль болатын бет.
Жер қыртысындағы масса үлестірілуі біркелкі емес болғандықтан геоидтің қарапайым геометриялық пішіні болмайды, бірақ ол айналма эллипсоидке (сфероидке) өте жақын болады. Айналма эллипсоид – эллипстің өзінің кіші өсі бойымен айналуы нәтижесінде алынатын фигура. Әдетте геоидтің беті континенттер ішінде эллипсоидтан жоғары, ал мұхиттарда одан төмен өтеді.
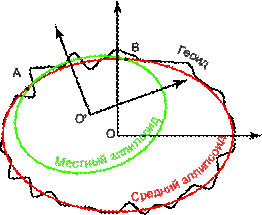
|
| 1.4 сурет- AB аймақтың жергілікті (референц-) эллипсоиды мен орта жер эллипсоидын анықтау |
Жердің нақты пішінін зерттеу геодезия мен гравиметрияның негізгі міндеттеріне жатады және геоидке ең жақын эллипсоидтың элементтерін табу мен геоидтің жеке бөліктерінің эллипсоидке қатысты орналасуын анықтаудан тұрады. Жер пішінін зерттеу үшін эллипсоидтың екі түрін енгізеді. Ол геоидті Жер бетінінің берілген бір аймақта жуықтайтын референц-эллипсоидтар және орташа жер эллипсоидтар, олардың геометриялық параметрлер нақты Жердің физикалық параметрлермен (массамен, сығылумен, инерция моменттерімен) анықталады. Топографиялық ерекшеліктер (таулар, ойпаттар) таңдап алынған эллипсоидтан ауытқулар ретінде қарастырылады.
Кестеде кейбір ең жиі қолданылатын орташа жер эллипсоидтарының параметрлері келтірілген.
| Аталуы | a, км | 1/f | GM, 1014 м3с-2 | J2, 10-3 | Ω, 10-5 рад/с |
| WGS 84 | 6378.137 | 298.25722356 | 3.986004418 | 1.08263 | 7.292115 |
| GRS 80 | 6378.137 | 298.257222101 | 3.986005 | 1.08263 | 7.292115 |
| IERS 96 | 6378.13649 | 298.25645 | 3.986004418 | 1.0826359 | 7.292115 |
Мұндағы a - экватор жазықтығында жататын эллипсоидтың үлкен жартыосі (Жердің экваторлық радиусы), f=(a-b)/a – эллипсоидтің геометриялық сығылуы (b - Жердің полюстік радиусы), G - гравитациялық тұрақты, J2 - Жердің динамикалық форм-факторы деп аталатын шама: J2 = (C-A)/(Ma2) (С мен А – Жердің бас инерция моменттері), Ω- Жер айналуының бұрыштық жылдамдығы.
Әр эллипсоид үшін келтірілген параметрлер тұрақтылар болып табылады, яғни олар дәлме-дәл белгілі деп есептеледі.
GPS серіктік навигация жүйесі координаттарды WGS84 (World Gеodetic System 1984) орташа жер эллипсоид жүйесінде береді. IERS96 (International Earth Rotation Service 1996) эллипсоидының базалары асаұзын радиоинтерферометрлердегі (БАҰР-дағы) бақылауларды өңдеу кезінде қолдануға ұсынылады. Геодезиялық жұмыстар үшін Геодезияның халықаралық ассоциациясының Ассамблеясымен 1979 жылы қабылданған GRS80 (Geodetic Reference System 1980) эллипсоиды қолдануға ұсынылады.
Жалпы айтсақ, Жер пішіні тасу әрекеті, тектоникалық плиталардың қозғалысы және өздік тербеліс салдарынан уақыт бойынша да өзгеріп отырады. Бірақ бұл өзгерістердің шамасы өте аз болғандықтан астрономиялық бақылауларға әсері жоқ деп есептеуге болады.
Осы аталған себептер салдарынан ілме сызығы жер бетінің кез келген нүктелері үшін сфероидтың радиус векторымен бағыттас бола бермейді. Сфероид бетіне түсірілген нормаль түзудің бағыты да ілме бағытына сәйкес болмауы мүмкін. Осыған байланысты географиялық ендіктің үш түрін қарастырады. Олар: астрономиялық, геоцентрлік және геодезиялық ендіктер.
Астрономиялық ендік деп берілген нүктедегі ілме мен Жер экваторы жазықтығы арасындағы бұрышты атаймыз (1.5 суреттегі φ бұрышы).
Геоцентрлік ендік деп жер бетіндегі берілген нүктеге жүргізілген радиус- вектор мен Жер экваторының жазықтығы арасындағы бұрышты атаймыз (1.5 суреттегі φ′ бұрышы).
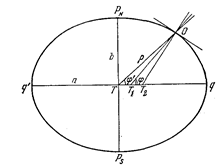 |
Геодезиялық ендік деп берілген нүктеде сфероид бетіне жүргізілген нормаль мен Жер экваторының жазықтығы арасындағы бұрышты атаймыз (1.5 суреттегі OT2q бұрышы).
1.5 сурет – Астрономиялық, геоцентрлік және геодезиялық ендіктерді анықтау
Астрономиялық өлшеулерден тек астрономиялық ендікті анықтауға болады. Геодезиялық және гравиметриялық өлшеулерден берілген нүктедегі ілменің ауытқуы, яғни ілме сызығының нормаль түзуден ауытқуы, ал оның негізінде геодезиялық ендік анықталады. Геоцентрлік ендік оны геодезиялық ендікпен байланыстыратын аналитикалық геометрияның формулалары негізінде анықталады. Астрономиялық ендік пен геодезиялық ендік арасындағы айырмашылық (аномальды жерлерді ескермейтін болсақ) 3″ аспайды. Сондықтан әдетте астрономиялық есептеулерде ол еске алынбайды да, астрономиялық пен геодезиялық ендіктер бірдей деп саналады.Ал геоцентрлік ендік пен астрономиялық ендік арасындағы айырмашылық 12′-қа дейін барады. Полюстар мен экваторда олардың айырмашылығы жоғалады.
1.4. АСПАН КООРДИНАТТАРЫНЫҢ ЖҮЙЕЛЕРІ
Аспан сферасы
Жоғарыда айтылғандай, астрономияның көптеген мәселелерін шешу үшін аспандағы шырақтарға дейінгі қашықтықты еске алмай, аспанды белгілі бір сфера (оны аспан сферасы деп атайды), ал аспандағы шырақтарды сол сфера бетінде орналасқан деп қарастырған жеткілікті әрі ыңғайлы.
Дата добавления: 2021-01-11; просмотров: 443;











