Основы биостатистики. Выборочный метод.
1. Статистика - это общественная наука, изучающая количественную сторону массовых общественных явлений в неразрывной связи их с качественной стороной.
В статистике свойство объектов или явлений, которое может быть наблюдаемо или измерено, называется признаком.
Статистика, изучающая вопросы, связанные с биологией, медициной, фармацией, гигиеной и здравоохранением, называется биостатистикой.
Роль биостатистики в практической и научной работе врача, медсестры, фармацевта велика.
Биостатистика применяет различные методы: сбор данных, их обобщение, анализ и подведение итогов, основанных на полученных наблюдениях.
Статистический анализ помогает добывать информацию из данных и оценивать качество этой информации.
Задачи биостатистики:
· количественное представление биологических фактов (измерение) – это выражение свойства отдельного биологического объекта в виде числа, варианты или значения переменной;
· обобщенное описание множества фактов (статистическое оценивание) – это расчет показателей и параметров, которые полноценно характеризуют свойства множества однотипных объектов или выборки;
· поиск закономерностей (проверка статистических гипотез) – это доказательство неслучайности отличий между сравниваемыми совокупностями, объектами, зависимости их характеристик от внешних или внутренних причин.
2. Первым этапом при проведении любого статистического исследования является сбор данных об анализируемом объекте или процессе в виде конкретных значений переменных.
Сбором статистических данных называется процесс получения информации об элементах исследуемой совокупности и их свойствах. Эти данные являются предметом статистической обработки и анализа.
Вторым этапом является анализ типов данных.
Типы данных: количественные, качественные и даты (рисунок 1.1).
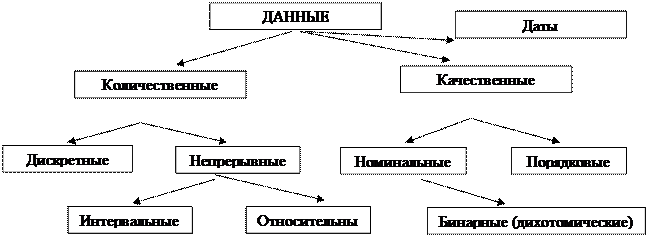
Рисунок 1.1. Классификация типов данных
Основные типы данных делятся на количественные и качественные.
Количественные данные в свою очередь подразделяются на дискретные (прерывные) и непрерывные.
Дискретные данные – количественные данные, которые представлены только в виде целого числа, т.е. не могут иметь дробную часть. Например: количество детей.
Непрерывные данные – это данные, которые получают при измерении на непрерывной шкале, т.е. теоретически они могут иметь дробную часть. Например: масса тела, рост, артериальное давление и т.д.
Непрерывные данные бывают интервальными и относительными.
Интервальные данные – вид непрерывных данных, которые измеряются в абсолютных величинах, имеющих физический смысл.
Относительные данные – вид непрерывных данных, отражающих долю изменения (увеличения или уменьшения) значения признака по отношению к исходному (или к какому-либо другому) значению этого признака. Эти данные являются безразмерными величинами или выражаются в процентах.
Качественные данные – подразделяются на номинальные и порядковые.
Номинальные данные – вид качественных данных, которые отражают условные коды неизмеряемых категорий (коды диагноза).
Порядковые данные - вид качественных данных, которые отражают условную степень выраженности какого-либо признака (стадии онкологических заболеваний, степени сердечной недостаточности).
Их основное отличие от дискретных количественных данных заключается в отсутствии пропорциональной шкалы для измерения выраженности признака.
Бинарные (дихотомические) данные - особо выделяемый вид качественных данных. Признак такого типа имеет лишь два возможных значения (пол, наличие или отсутствие какого-либо заболевания).
Особым видом данных являются даты. Поскольку в ряде случаев бывает необходимо произвести с ними некоторые арифметические действия (вычисление абсолютного периода времени между двумя событиями по датам этих событий).
Иногда выделяют также некоторые особые подтипы данных, являющиеся частными случаями вышеперечисленных типов: ранги, очки, визуальные аналоговые шкалы, цензурированные данные.
Перед тем как проводить угубленный статистический анализ, важно провести предварительный анализ данных. На этом этапе для сжатия и систематизации набора данных используют графические методы. Это позволяет оценить особенности набора данных и выявить аномалии, т.е. выбрать для дальнейшого анализа подходящие статистические методы.
Дискретные данные могут быть представлены в виде таблицы, столбиковой диаграммы, пиктограммы, круговой диаграммы, точечного рисунка.
Непрерывные данные могут быть представлены в виде группированной выборки, гистограммы, диаграммы «стебель с листьями» или «ящик с усами», кривой Лоренца и т.д.
Смешанные данные могут быть представлены в виде диаграммы рассеяния.
Графические методы представления данных.
График, в котором статистические данные изображаются различными геометрическими фигурами, называется диаграммой.
Виды наиболее часто используемых диаграмм:
· Диаграммы, изображающие динамику явления, выраженного в показателях интенсивности, соотношения, наглядности, средних или абсолютных величинах, называются линейными (рисунок 1.2).
Рисунок 1.2. Линейные диаграммы (график)
· Вид линейной диаграммы, применяемой для изображения динамики явления за замкнутый цикл времени (сутки, неделя, месяц, год), называется радиальной (рисунок 1.3).
Рисунок 1.3. Радиальные диаграммы
· Диаграммы, изображающие динамику или статику явления в соответствии с избранным масштабом, называются столбиковыми (рисунок 1.4).
Рисунок 1.4. Столбиковые диаграммы
· Диаграммы, изображающие структуру явления, выраженного экстенсивными показателями, и представляющие собой прямоугольник, в котором цветом выделены составляющие его части в соответствии с их удельным весом, называются внутристолбиковыми (рисунок 1.5).

Рисунок 1.5. Внутристолбиковая диаграмма
График, который представляет собой смесь диаграммы и таблицы, эффективен для отображения данных по увеличению порядка величины, называется графиком «стебель и листья» (рисунок 1.6).
| 1,0 | ||
| 1,1 | ||
| 1,2 | ||
| 1,3 | ||
| 1,4 | ||
| 1,5 | ||
| 1,6 | ||
| 1,7 | ||
| 1,8 | ||
| 1,9 | ||
| 2,0 | ||
| 2,1 | ||
| 2,2 |
Рисунок 1.6. График «стебель и листья»
График, который представляет собой прямоугольник, где две параллельных стороны соответствуют верхнему и нижнему квартилям данных, а линии, начинающиеся в конце прямоугольника, показывают минимальные и максимальные значения, называется график «ящик с усами» (рисунок 1.7).
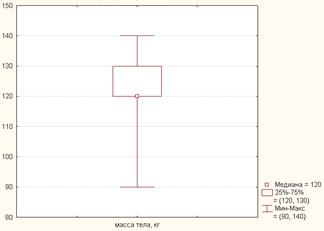
Рисунок 1.7. График «ящик с усами»
3. Измерение – это процедура сравнения объектов по определенным показателям или характеристикам (признакам, атрибутам).
Шкала – необходимый, обязательный элемент измерительной процедуры.
Основные типы измерительных шкал, применяемые в медико-биологических исследованиях:
· номинальная или шкала наименований используетя для классификации свойств объекта, присвоения им числовых, буквенных и иных символьных характеристик (пол, национальность, цвет глаз, цвет волос, диагноз и т.д.);
· порядковая или ранговая – упорядочивает значения признака (шкала стадий гипертонической болезни по Мясникову, шкала степеней сердечной недостаточности по Стражеско-Василенко-Лангу, шкала степени выраженности коронарной недостаточности по Фогельсону и др.);
· интервальная – показывает «размах» отдельных измерений признака (время, шкала температур, тестовые баллы);
· шкала отношений – выявляет соотношение измеренных значений признака (рост, вес, время реакции, количество выполненных заданий теста).
4. Статистическая совокупность – совокупность однородных по какому-либо признаку объектов, ограниченных пространством и временем (число детей, родившихся в стране в течение определенного года; число жителей одного города; число больных онкозаболеваниями в данной стране и т.д.).
При медико-биологических, клинических, фармацевтических и других исследованиях в распоряжении исследователя практически никогда нет полной группы объектов, т.е. невозможно провести сплошное наблюдение, поэтому для исследования используют выборочный метод.
Выборочный метод – метод статистического обследования, при котором из статистической совокупности выбирают ограниченное число объектов и их подвергают изучению.
Выборочный метод находит широкое применение в медицине, биологии, здравоохранении и фармации. Например: нет возможности обследовать всех больных с определенной патологией, поэтому обследуют их некоторое число; нет возможности проверить все лекарственные препараты на соответствие стандарту, поэтому проводят их выборочный контроль и т.д.
Генеральная статистическая совокупность - это совокупность, которая состоит из бесконечно большого числа элементов. Например: все больные с данной патологией; все жители данной территории и т.д.
Выборочная совокупность (выборка) - это совокупность, которая состоит из части выбранных элементов наблюдения, способных охарактеризовать всю генеральную совокупность.
Объем совокупности- это общее число элементов наблюдения. Объем генеральной совокупности обозначается «N», объем выборочной совокупности – «n». Если n≤30, то выборка считается малой.
Элемент наблюдения - это каждый частный случай явления, которое изучается.
Выборочный метод исследования является единственно возможным в случае бесконечной генеральной совокупности или в случае, когда исследование связано с уничтожением наблюдаемых объектов (например, проверка лекарственных препаратов). Кроме того, он позволяет существенно экономить затраты ресурсов. Недостатком этого метода является появление ошибок исследования, которые связаны с тем, что изучается только часть объекта.
Главным свойством выборки является показательность(репрезентативность),т.е. ее свойство достаточно хорошо воспроизводить генеральную совокупность. Репрезентативность достигается, если объекты генеральной совокупности имеют одинаковую вероятностью попадания в выборку.
Виды показательности:
· качественная – это соответствие признаков элементов наблюдения в выборочной и генеральной совокупностях.
· количественная- это достаточное число наблюдений.
5. Первым шагом систематизации материалов статистического наблюдения является определение статистического распределения выборки.
Статистическое распределение выборки (или вариационный ряд) представляет собой таблицу, состоящую из двух столбцов (таблица 1.1).
В первом столбце записываются значения варьирующего признака, называемые вариантами и обозначаемые «xi», а во втором столбце записываются числа, называемые частотами и обозначаемые «νi», показывающие сколько раз встречается каждый вариант.
Таблица 1.1.
| Варианты (xi) | Частоты (νi) |
| ... | ... |
| ... | ... |
| ... | ... |
| Всего: | n=Σ νi |
Варьирующие признаки могут иметь дискретный и непрерывный характер.
Варианты признаков, которые являются целыми числами, называют дискретными. Например, число детей в семье, число пациентов, количество ампул в упаковке и т.д.,
Если варианты вариационного ряда выражены в виде дискретных величин, то такой вариационный ряд называют дискретным.
Пример 1.1. В результате отдельных испытаний активности тетрациклина гидрохлорида были получены значения xi (в ED/мг): 925, 940, 760, 905, 995, 965, 940, 925, 940, 940, 905.
Располагая значения активности и частоты в порядке возрастания, получим дискретный вариационный ряд (таблица 1.2):
Таблица 1.2.
| Варианты (xi) | Частоты (νi) |
| Всего: | n=10 |
Дискретный вариационный ряд можно представить графически в виде многоугольника, называемого полигоном (рисунок 1.8).
|
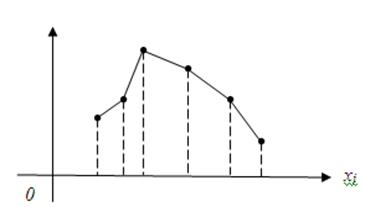
Рисунок 1.8. Полигон
Варианты признаков, которые могут принимать любые значения в определенном интервале, называют непрерывными. Например, артериальное давление, рост, вес, заработная плата и др.
Для непрерывных признаков строятся интервальные вариационные ряды. Минимальное значение признака в заданном интервале называют нижней границей интервала, а максимальное – верхней.
Пример 1.2. В таблице 1.3 приведен интервальный вариационный ряд роста (xi) мужчин.
Таблица 1.3.
| Варианты (xi), см | Частоты (νi) |
| 150-155 | |
| 155-160 | |
| 160-165 | |
| 165-170 | |
| 170-175 | |
| 175-180 | |
| 180-185 | |
| 185-190 |
Интервальный вариационный ряд можно представить графически в виде ступенчатой фигуры, называемой гистограммой (рисунок 1.9).
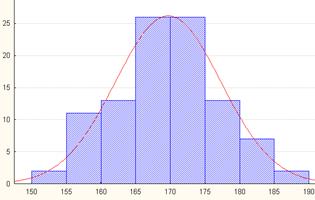
Рисунок 1.9. Гистограмма
При большом числе наблюдений интервальные вариационные ряды строят и для дискретных признаков.
6. Вариационный ряд характеризуется показателями центральной тенденции и показателями разнообразия.
К показателям центральной тенденции относятся средние и структурные величины.
Средние величины:
· средняя арифметическая простая
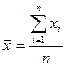 , (1.1)
, (1.1)
где n - общее число членов ряда;
· средняя арифметическая взвешенная
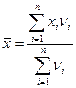 , (1.2)
, (1.2)
где νi – частоты;
· средняя геометрическая простая
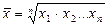 ; (1.3)
; (1.3)
· средняя квадратическая простая
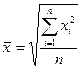 ; (1.4)
; (1.4)
· средняя квадратическая взвешенная
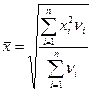 . (1.5)
. (1.5)
Структурные величины:
· мода (Мо) – варианта с наибольшей частотой.
· медиана (Ме) – варианта, находящаяся в середине ряда.
· квантили - отдельные равные части, на которые разбивается вариационный ряд:
- квартили – величины, делящие вариационный ряд на четыре равные части;
- квинтили - величины, делящие вариационный ряд на пять равных частей;
- децили - величины, делящие вариационный ряд на десять равных частей;
- процентили - величины, делящие вариационный ряд на сто равных частей (рисунок 1.10).
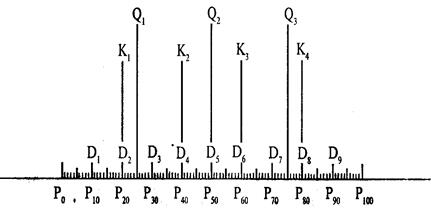
Рисунок 1.10. Структурные характеристики вариационного ряда
Нижний квартиль (Q1) или 25-й процентиль (P25) - это значение случайной величины, ниже которого находится 25% выборки.
Номер нижнего квартиля определяется по формуле:
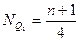 . (1.6)
. (1.6)
Верхний квартиль (Q3) или 75-й процентиль (P75) - это значение случайной величины, выше которого находится 25% выборки.
Номер верхнего квартиля определяется по формуле:
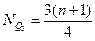 . (1.7)
. (1.7)
Если номер квартиля получится дробным, то его можно округлить до ближайшего целого.
К показателям разнообразия относятся:
· размах вариационного ряда
R=xmax– xmin,(1.8)
где xmax, xmin– наибольшее и наименьшее значения вариант соответственно;
· дисперсия - мера разброса случайной величины от ее среднего значения:
- если выборка задана вариационным рядом, то выборочная дисперсия определяется по формуле:
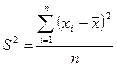 ; (1.9)
; (1.9)
- если выборка задана в виде таблицы, то выборочная дисперсия определяется по формуле:
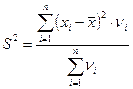 ; (1.10)
; (1.10)
· среднее квадратическое отклонение
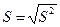 ; (1.11)
; (1.11)
· коэффициент вариации - мера разброса случайной величины, выраженная в процентах:
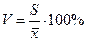 . (1.12)
. (1.12)
Если V≤33%, то выборка считается однородной.
Статистические характеристики удобно показать с помощью графика «ящик с усами».
Например, для выборочных данных о росте 30-летних женщин были построены следующие графики (рисунок 1.11 a, b).
При анализе таких графиков обязательно нужно обращать внимание на «легенду», т.е. условные обозначения, которые приводятся в нижней части графика.
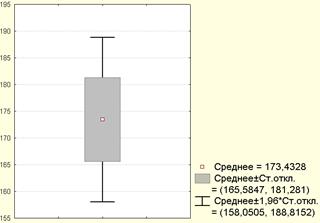
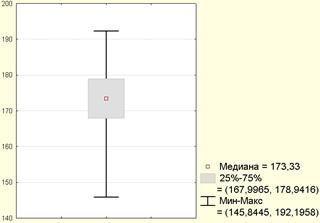
a b
Рисунок 1.11. Отображение статистических характеристик на графике «ящик с усами»
На первом графике (рисунок 1.11, а) приведены среднее, минимальное и максимальное значения, а также стандартное отклонение. На втором
графике (рисунок 1.11, b) приведены значения медианы, 25-го и 75-го процентилей.
4. Иллюстративный материал:презентация, слайды.
5. Литература:
1. Жижин К.С. Медицинская статистика: Учебное пособие / Ростов н/д: Феникс, 2007. - 160 с.
2. Петри А., Сэбин К. Наглядная медицинская статистика/ пер. с англ. под ред. В.П. Леонова. 2-е изд., перераб. и доп. - М.: ГЭОТАР-Медиа, 2009. - 168 с.
3. Платонов А.Е. Статистический анализ в медицине и биологии: задачи, терминология, логика, компьютерные методы. - М.: Издательство РАМН, 2000. - 52 с.
4. Реброва О.Ю. Статистический анализ медицинских данных. Применение пакета прикладных программ STATISTICA. - М.: МедиаСфера, 2002. - 312 с.
5. Рокицкий П.Ф. Биологическая статистика. Изд. 3-е, испр. Минск, «Высшая школа», 1973. - 320 с.
6. http://www.biometrica.tomsk.ru
7. http://ru.wikipedia.org
6. Контрольные вопросы:
1. Что такое «биостатистика»?
2. Что называется сбором статистических данных?
3. Какие типы статистических данных Вы знаете?
4. Какие типы измерительных шкал применяются в медико-биологических исследованиях?
5. Что такое генеральная и выборочная совокупности?
6. Что такое вариационный ряд?
7. Какие показатели вариационного ряда Вы знаете?
ЛЕКЦИЯ № 2
1. Тема: Основы теории проверки статистических гипотез. Параметрические критерии.
2. Цель: Ознакомить студентов с основными понятиями теории проверки статистических гипотез, а также с t-критерием Стьюдента.
План лекции:
1. Статистические гипотезы, применительно к медико-биологическим исследованиям.
2. Уровень значимости, доверительная вероятность, мощность критерия.
3. Схема проверки статистических гипотез.
4. t-критерий Стьюдента для анализа биомедицинских данных.
5. Схема применения двухвыборочного t-критерия Стьюдента.
6. Схема применения парного t-критерия Стьюдента.
3. Тезисы лекции:
1. В прикладных задачах часто требуется по наблюдениям выборки высказать некоторое суждение (гипотезу) относительно интересующих экспериментатора характеристик генеральной совокупности, из которой эта выборка извлечена. То есть, речь идет о проверке статистических гипотез.
Гипотеза – это некоторое предположение о параметрах известных распределений (параметрическая) или о виде неизвестного закона распределения (непараметрическая) случайных величин, выдвигаемое в качестве предварительного, условного объяснения.
Теория проверки статистических гипотез является основным инструментом доказательной, а не интуитивной медицины.
Задачи медицинских и биологических исследований, для решения которых необходимо сформулировать статистические гипотезы:
· анализ соответствия распределения значений признака в изучаемой группе какому-либо определенному закону (анализ соответствия распределения нормальному закону);
· сравнение групп по параметрам распределений признака (по средним значениям, дисперсиям).
Например, при проверке статистических гипотез можно получить ответ на следующий вопрос. В двух однородных группах больных гриппом была проведена вакцинация: одной лекрственным средством «А», а другой - «В», среднее время выздоровления в группах неодинаково. Указывает ли это обстоятельство на то, что одно противогриппозное средство по эффективности превосходит другое или же выявленное различие случайно?
Для решения любой подобной задачи выдвигаются две статистические гипотезы:
· нулевая гипотеза Н0 - гипотеза об отсутствии различий между группами, либо об определенных значениях параметров, либо о соответствии распределения нормальному закону;
· альтернативная гипотеза Н1 - гипотеза о существовании различий между группами, либо об отличающихся от заданных значениях параметров, либо о несоответствии распределения нормальному закону.
Нулевая гипотеза формулируется таким образом, чтобы она была противоположной той исследовательской (медицинской, биологической) гипотезе, которая послужила поводом для проведения исследования.
Для проверки нулевой гипотезы применяют статистические методы (тесты, критерии).
Статистика – это функция от выборочных наблюдений, на основе которой принимается или отвергается нулевая гипотеза.
Статистическими критериями называются правила, согласно которым выясняется, соответствует или нет интересующая нас гипотеза опытным данным.
Статистические критерии - это наиболее широко применяемые статистические средства.
Значение критерия, которое рассчитано по выборочной совокупности, подчиняющейся определённому закону распределения, называется наблюдаемым.
Множество возможных значений статистического критерия, при которых основная гипотеза принимается, называется областью принятия.
Множество возможных значений статистического критерия, при которых основная гипотеза отвергается, называется критической областью.
Точки, разграничивающие критическую область и область принятия гипотезы, называются критическими точками.
При проверке статистических гипотез возникают следующие виды ошибок:
· ошибка первого рода – это вероятность отвергнуть правильную нулевую гипотезу;
· ошибка второго рода – это вероятность принять неправильную нулевую гипотезу.
2. Уровень значимости - это максимально приемлемая для исследователя вероятность ошибочно отклонить нулевую гипотезу, когда на самом деле она верна, т.е. допускаемая исследователем величина ошибки первого рода.
При иссследованиях в фармации, медицине и биологии используется величина уровня значимости, равная 0,05. При разработке стандартов используют уровень значимости равный 0,01.
Уровень значимости или вероятность ошибки первого рода обозначается через «р», а вероятность ошибки второго рода - через «γ».
Доверительная вероятность (γ) - это вероятность не совершить ошибку первого рода и принять верную гипотезу Н0 (γ=1-р).
Важнейшей характеристикой любого статистического критерия является его мощность. Мощностью критерия называется его способность правильно исключать ложную гипотезу.
Мощность оценивается вероятностью 1-γ, где γ - вероятность ошибки второго рода.
3. Схема проверки статистических гипотез:
1) Выдвигаются две гипотезы: основная (нулевая) «Н0» и альтернативная (конкурирующая) «Н1».
2) Задается уровень значимости «р». Статистический вывод никогда не может быть сделан со стопроцентной уверенностью. Всегда допускается риск принятия неправильного решения. При проверке статистических гипотез мерой такого риска является уровень значимости «р».
3) По исходным данным, т.е. по выборке, вычисляется наблюдаемое (эмпирическое, расчетное) значение критерия.
4) По специальным статистическим таблицам определяется табличное (критическое) значение критерия.
5) Путем сравнения наблюдаемых и табличных значений делается вывод о правильности той или иной гипотезы.
4. В процессе медико-биологических исследований часто возникает проблема сравнения результатов обследования (например, в контрольной и экспериментальной группах или до и после эксперимента).
Для решения этой проблемы существует большое количество статистических критериев. Каждый из них имеет свою специфику, отличаясь друг от друга (например, типами данных, объемами выборок, количеством сравниваемых выборок, качеством сравниваемых выборок (зависимая и независимая) и др.).
Наиболее популярным из таких критериев является t-критерий Стьюдента, который применяется примерно в 30-40% научных медицинских работ (рисунок 2.1).

Рисунок 2.1. Соотношение статистических методов, используемых в медицинских научных работах
t-критерий Стьюдента - метод проверки однородности выборок, позволяет принять или отвергнуть гипотезу о равенстве средних двух выборок ( 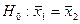 ).
).
Данный критерий был разработан английским химиком Уильямом Госсеттом (1876-1936 гг.) (рисунок 2.2) для оценки качества пива в компании «Гиннес».
Статья Госсета вышла в 1908 г. в журнале «Биометрика» под псевдонимом «Student» (Студент).

Рисунок 2.2. У. Госсет
t-критерий Стьюдента используется:
· при проверке гипотезы о равенстве средних двух независимых выборок (двухвыборочный t-критерий). Вэтом случае анализируются контрольная и экспериментальная выборки разных объемов. Например, группа больных сахарным диабетом и группа здоровых людей;
· при проверке гипотезы о равенстве средних двух зависимых выборок (парный t-критерий). В этом случае анализируется одна и та же выборка, но до и после эксперимента.Например, средняя частота пульса у одних и тех же пациентов до и после приема антиаритмического препарата.
Применение критерия Стьюдента возможно, если выполняются следующие два условия:
· рассматриваемые выборки имеют нормальное распределение;
· дисперсии рассматриваемых выборок равны.
Исследователями установлено, что оба условия одновременно выполняются лишь в 4-5% случаев медико-биологических экспериментов.
В то же время анализ диссертаций, научных работ, статей, опубликованных в медицинских журналах, показывает, что t-критерий Стьюдента используется при проведении статистических расчетов в 50% работ.
5. Схема применения двухвыборочного критерия Стьюдента:
1) Н0: 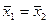 .
.
Н1: 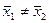 .
.
1) р=0,05 - уровень значимости.
2) 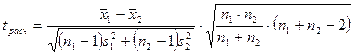 , (2.1)
, (2.1)
где n1, n2 - объемы рассматриваемых выборок, 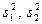 - дисперсии рассматриваемых выборок,
- дисперсии рассматриваемых выборок, 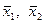 - сравниваемые средние значения выборок.
- сравниваемые средние значения выборок.
4) 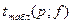 ,
,
где f= n1+n2-2- число степеней свободы (табличное значение).
5) Если 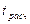 ≤
≤ 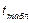 , то «H0» принимается.
, то «H0» принимается.
Если 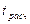 >
> 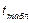 , то «H0» отвергается.
, то «H0» отвергается.
Критерий Стьюдента применяется в случае малых выборок (n1,2≤30).
Пример 2.1. Если при родах шейка матки долго не раскрывается, то продолжительность родов увеличивается и может возникнуть необходимость кесарева сечения. Ученые решили выяснить, ускоряет ли гель с простагландином Е2 раскрытие шейки матки. В исследование вошло 2 группы рожениц. Роженицам первой группы вводили в шейку матки гель с простагландином Е2, роженицам второй группы вводили гель-плацебо. В обеих группах было по 21 роженице возраст, рост и сроки беременности были примерно одинаковы. Роды в группе, получавшей гель с простагландином Е2, длились в среднем 8,5 часов (стандартное отклонение 4,7 часа), в контрольной группе - 13,9 часа (стандартное отклонение 4,1 часа). Можно ли утверждать, что гель с простагландином Е2 сокращал продолжительность родов?
Решение.
1) Н0: 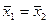 .
.
Н1: 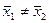 .
.
2) р=0,05 - уровень значимости.
3) Используем формулу (2.1).
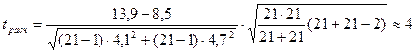 .
.
4) 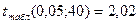 .
.
5) Т.к. 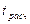 >
> 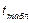 , то «H0» отвергается, т.е. гель с простагландином Е2 сокращал продолжительность родов.
, то «H0» отвергается, т.е. гель с простагландином Е2 сокращал продолжительность родов.
6. Схема применения парного критерия Стьюдента:
1) Н0: 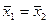 .
.
Н1: 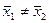 .
.
2) р=0,05- уровень значимости.
3) 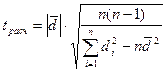 , (2.2)
, (2.2)
где 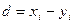 - разности между соответствующими значениями пар переменных,
- разности между соответствующими значениями пар переменных, 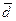 - среднее значение этих разностей, n - объем выборки.
- среднее значение этих разностей, n - объем выборки.
4) 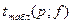 ,
,
где f= n-1- число степеней свободы (табличное значение).
5) Если 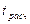 ≤
≤ 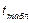 , то «H0» принимается.
, то «H0» принимается.
Если 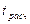 >
> 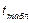 , то «H0» отвергается.
, то «H0» отвергается.
Иногда сравнение выборочных средних проводится по следующей формуле:
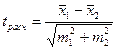 , (2.3)
, (2.3)
где 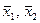 - сравниваемые средние величины; m1 и m2 - ошибки сравниваемых средних величин.
- сравниваемые средние величины; m1 и m2 - ошибки сравниваемых средних величин.
Если tрасч³2, то «H0» отвергается.
Пример 2.2. Для оценки эффективности нового гипогликемического препарата были проведены измерения уровня глюкозы в крови пациентов, страдающих сахарным диабетом, до и после приема препарата:
| № пациента | Уровень глюкозы в крови, моль/л | |
| до приема препарата | после приема препарата | |
| 9,6 | 5,7 | |
| 8,1 | 4,2 | |
| 8,8 | 6,4 | |
| 7,9 | 5,5 | |
| 9,2 | 5,3 | |
| 8,0 | 5,2 | |
| 8,4 | 5,1 | |
| 10,1 | 5,9 | |
| 7,8 | 7,5 | |
| 8,1 | 5,0 | |
| Среднее значение | 8,6 | 5,6 |
Решение.
1) Н0: 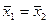 .
.
Н1: 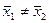 .
.
2) р=0,05- уровень значимости.
3)
| № пациента | Уровень глюкозы в крови, моль/л | Разность значений 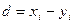
|
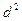
| |
| до приема препарата | после приема препарата | |||
| 9,6 | 5,7 | 3,9 | 15,21 | |
| 8,1 | 4,2 | 3,9 | 15,21 | |
| 8,8 | 6,4 | 2,4 | 5,76 | |
| 7,9 | 5,5 | 2,4 | 5,76 | |
| 9,2 | 5,3 | 3,9 | 15,21 | |
| 8,0 | 5,2 | 2,8 | 7,84 | |
| 8,4 | 5,1 | 3,3 | 10,89 | |
| 10,1 | 5,9 | 4,2 | 17,64 | |
| 7,8 | 7,5 | 0,3 | 0,09 | |
| 8,1 | 5,0 | 3,1 | 9,61 | |
| Сумма | 30,2 | 103,22 |
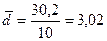 .
.
Используем формулу (2.2).
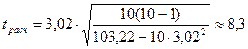 .
.
4) 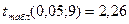 .
.
5) Т.к. 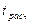 >
> 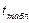 , то «H0» отвергается, т.е. уровень глюкозы в крови после приема препарата снизился, значит новое средство эффективно.
, то «H0» отвергается, т.е. уровень глюкозы в крови после приема препарата снизился, значит новое средство эффективно.
Пример 2.3. У студентов - медиков проводилось исследование пульса до и после сдачи экзамена. Частота пульса до экзамена составила 98,8 ±4,0, а после экзамена 84,0 ±5,0. Можно ли считать, что после экзамена частота пульса снижается и приближается к норме?
Решение.
1) Н0: 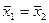 .
.
Н1: 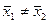 .
.
2) р=0,05.
3) Используем формулу (2.3).
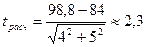 .
.
4) Т.к. tрасч>2, то «H0» отвергается, т.е. после экзамена частота пульса снижается и приближается к норме.
4. Иллюстративный материал:презентация, слайды.
5. Литература:
1. Васильева Л.А. Статистические методы в биологии, медицине и сельском хозяйстве: Учеб. пособие для вузов. - Новосибирск, Новосибирский Государственный университет, 2007. - 128 с
2. Герасимов А.Н. Медицинская статистика: Учеб. Пособие. – М.: МИА, 2007. - 480 с.
3. Гмурман В.Е. Теория вероятностей и математическая статистика: Учеб. пособие для вузов.- 9-е изд., стер. - М.: Высш. шк., 2003. - 479 с.
4. Кендалл М., Стюарт А. Статистические выводы и связи. - М.: Наука, 1973. - 470 с.
5. Лобоцкая Н.Л. Высшая математика. / Н.Л. Лобоцкая, Ю.В. Морозов, А.А. Дунаев. - Мн.: Высшая школа, 1987. - 319 с.
6. Медик В.А., Токмачев М.С., Фишман Б.Б. Статистика в медицине и биологии: Руководство. В 2-х томах/ Под ред. Ю.М. Комарова. Т. 1. Теоретическая статистика. - М.: Медицина, 2000. - 412 с.
7. Основы высшей математики и математической статистики: Учебник / И.В. Павлушкин и соавт. - М.: ГЭОТАР-МЕД, 2004. - 424 с.
8. Петри А., Сэбин К. Наглядная медицинская статистика / А. Петри, К. Сэбин; пер. с англ. под ред. В.П. Леонова. 2-е изд., перераб. и доп. - М.: ГЭОТАР-Медиа, 2009. - 168 с.
9. http://matstats.ru/
6. Контрольные вопросы:
1. Что называется статистической гипотезой? Какие виды статистических гипотез Вы знаете?
2. Что называется ошибкой ошибкой первого и второго рода?
3. Что называется доверительной
| <== предыдущая лекция | | | следующая лекция ==> |
| Определение наилучших решений внутри области компромиссов. | | | Анализ принципиальной тепловой схемы ТЭЦ. Порядок расчета |
Дата добавления: 2016-10-07; просмотров: 16026;











