Определение наилучших решений внутри области компромиссов.

Получаемая в результате пересечения указанных подмножеств оптимальных параметров гарантируемая область компромиссов включает в себя все те значения параметров, которые соответствуют наилучшей совокупной эффективности ЛА во всем диапазоне вероятных значений исходных проектных данных. Следовательно, в случае выбора значений параметров ГТД в пределах этой области при любом сочетании исходных данных обеспечивается практически максимально возможная эффективность ЛА. Выбранные таким образом параметры устойчивы к неопределенности исходной проектной информации. Однако полученная при этом область компромиссов может сказаться слишком широкой (см.рис.6.13).

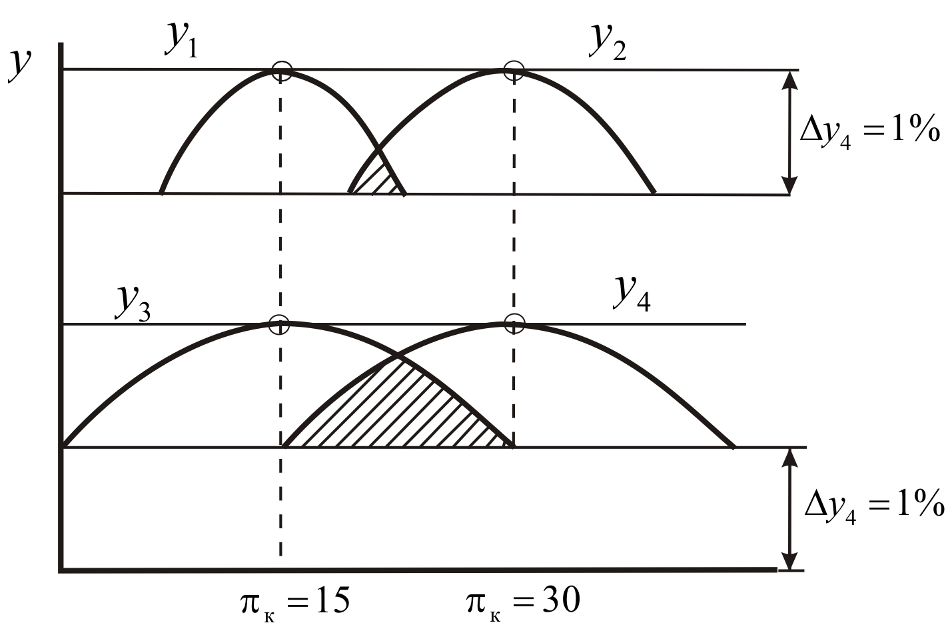
Рис.6.13 Ширина области компромиссов

Как видно, ширина области компромиссов зависит от “природы” топологии оптимума (и его пологости). Для того чтобы сузить и найти наиболее устойчивые значения параметров ГТД ( 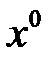) следует воспользоваться каким-либо принципом оптимальности. В большинстве случаев для выбора параметров ГТД оказывается рациональным использовать минимаксный принцип оптимальности (принцип Севиджа), позволяющий быстро сузить область поиска и гарантирующий надежность выбираемого рационального решения.

Запишем выражение реализующее этот принцип ,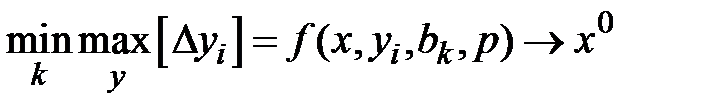

где:

х – вектор оптимизируемых параметров ( 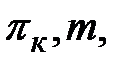и т.д.);

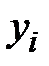- критерий комплекса оценки ЛА ( 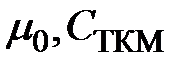и др.);

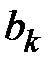- исходные данные неоднозначной величины ( );

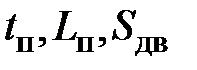p – исходные данные однозначной величины ( 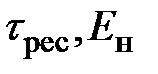и др.);

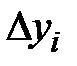- степень отклонения от экстремума y;

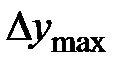- находится для каждого y(max) при переборе всех ;

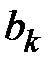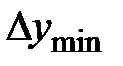- находится для искомого 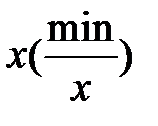среди всех .

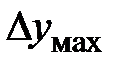Т.о. в этом случае для всех вариантов x отыскивается минимум тех величин ( 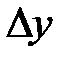), которые максимальны для всех рассматриваемых критериев оценки ЛА ( ).

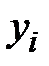При выборе наиболее устойчивых значений оптимальных параметров ГТД применяют и другие принципы оптимальности, как, например, минимализация средних, а не максимальных значений 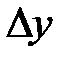(принцип Лапласа).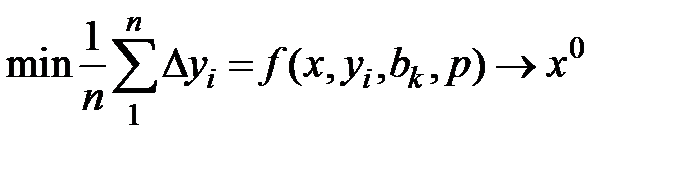

Минимализация среднего арифметического между максимальным и минимальным значениями (принцип Гурвица)

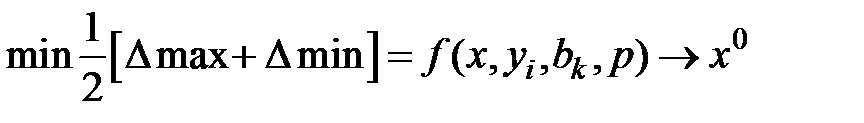
Однако последние два сужают область поиска значительно слабее.

Одна из возможных ситуаций при определении области компромиссов - “выпадение” изолинии одного из критериев, даже с учетом 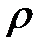, из области пересечений. В этом случае данный критерий можно перевести в ограничения, т.е. оговорить его допустимый уровень. Теоретически возможен предельный случай – полного отсутствия пересечений изолинии всех рассматриваемых критериев. В этом случае возможно использовать только один единственный принцип оптимальности, заключающийся в выделении главного критерия. При этом проводят скалярную максимализацию главного критерия при условии, что уровень остальных критериев эффективности должен быть не менее допустимого, т.е. переводят их в ограничения. Следует отметить, что при оптимизации параметров авиационных ГТД этот случай в принципе не встречается, хотя главный критерий иногда выделяют.