Формальные модели синтаксической структуры предложения

Представления о бинарных синтаксических связях используются в двух известных моделях синтаксической структуры: графах зависимостей и графах непосредственных составляющих. В настоящее время эти две формы представления синтаксической структуры остаются основными. Они используются в чистом виде или очень часто – в смешанных формах, сочетающих в себе свойства обоих графов.

Грамматика зависимостей - указание для каждого слова тех слов, которые ему непосредственно подчинены.

Дерево синтаксических зависимостей - дерево, множество узлов которого служит множеством вхождений слов в предложение. Деревом называется множество, между элементами которого (узлами) установлено бинарное отношение (отношение подчинения), графически изображаемое стрелками, идущими от подчиняющих узлов к подчиненным. Дерево обладает следующими свойствами:

· среди узлов имеется один - корень - неподчиненный никакому другому узлу;

· каждый из остальных узлов подчинен точно одному узлу;

· нельзя, отправившись из какого-либо узла вдоль стрелок вернутся в тот же узел.

Дерево зависимостей обычно используется в описаниях языков со свободным порядком слов, в частности, русского. Стрелки дерева обычно помечаются символами синтаксических отношений (предикативное, определительное и т.п.).

Метод непосредственных составляющих (НС). Для описания синтаксической структуры предложения выделяются группы слов, функционирующие как отдельные синтаксические единицы - составляющие.

Система составляющих - это множество отрезков предложения которое обладает тем свойством, что каждые два входящих в него отрезка либо не пересекаются либо один из них содержится в другом.

Одна из НС - ядро конструкции, остальные - маргинальные элементы. При графическом изображении система составляющих тоже приобретает вид дерева (дерева непосредственных составляющих — ДНС). ДНС используются преимущественно. в описаниях языков с жестким порядком слов. Составляющие обычно помечаются символами грамматических категорий (именная группа, группа переходного глагола и т.п.)

Трансформационная грамматика (грамматика деревьев) служит не для порождения предложений, а для преобразования деревьев, интерпретируемых как деревья подчинения или деревья составляющих, например грамматика - система правил преобразования деревьев, интерпретируемых как «чистые» деревья подчинения предложений (без линейного порядка слов).

Три уровня описания

1) правила НС

2) трансформационные правила

3) морфологические правила

Допущения:

Синтаксическая система может быть разбита на ряд подсистем, одна из которых - исходная (ядерная), остальные - производные. Ядерная представляет собой набор предложений (утвердительных, простых, с глаголом в изъявительной форме, активного залога, настоящего времени). Ядерное предложение (ЯП) описывает элементарные ситуации, а класс ЯП - все множество элементарных ситуаций. Любой сложный синтаксический тип можно получить при применении упорядоченного набора обязательных и факультативных трансформаций к ЯП.

Представление синтаксической структуры предложения - указание ядерного типа, лежащего в основе предложения и трансформаций, которые к нему применялись, а также их последовательности.

Метод явился основой порождающей грамматики Хомского. Порождающая грамматика Хомского, представляющая собой упорядоченную систему Г =(V,W,J,R), где V и W - непересекающиеся конечные множества - основное (терминальное) и вспомогательное (нетерминальное), J - элемент W, называемый начальным символом и R - конечное множество правил вида j(r)y, где j и y - цепочки (конечные последовательности) из основных и вспомогательных символов. Множество тех цепочек из основных символов, которые выводимы в Г из ее начального символа, называют языком, порождаемым грамматикой Г и обозначают L(Г). Если все правила Г имеют вид caw(r)cyw , где a - вспомогательный символ, y - непустая цепочка, c и w - произвольные цепочки, то Г называется грамматикой составляющих или грамматикой непосредственно составляющих (ГНС).

В грамматиках составляющих на каждом шаге вывода заменяется только один символ, поэтому в них с каждым выводом ассоциируется так называемое дерево вывода. Корень дерева отвечает начальному символу. Каждому символу цепочки, на которую заменяется начальный символ на первом шаге вывода, ставится в соответствие узел дерева, и к нему проводится дуга из корня. Для тех из полученных узлов, которые помечены вспомогательными символами, делается аналогичное построение и т.д. Дерево вывода, рассматриваемое как дерево составляющих предложения, задает на нем систему составляющих. Это делает грамматики составляющих хорошим инструментом для описания естественных и искусственных языков.

Чаще всего основные символы интерпретируются как слова, вспомогательные - как символы грамматических категорий, начальный символ - как символ категории «предложение».

Для построения формальных моделей синтаксической структуры введем несколько понятий.

Произвольную (непустую) по­следовательность словоформ будем называть цепочкой. Число словоформ в цепочке ω будем называть длиной цепочки и обозначать |ω|. Если для каких-либо цепочек ω, φ, η₁, η₂, имеет место равенство ω=η₁φη₂, то будем говорить, что цепочка φ, входит в цепочку ω. Вхождения словоформ в цепочку будем называть ее точками. Если α и β — точки одной и той же цепоч­ки ω = η₁αη₂ = ξ₁βξ₂ и если при этом |η₁| < |ξ₁|, то будем писать α < β или β > α и говорить, что α расположена левее β, а β — правее α. Для любых двух точек α и β цепочки ω, таких, что α ≤ β, введем понятие отрезка цепочки ω, представляющего мно­жество точек ξ, удовлетворяющих неравенствам α ≤ ξ ≤ β.

Граф зависимости

Описание структур в форме классического графа зависимостей хорошо соответствует русской грамматической традиции: оно основывается на понятии бинарного словосочетания в предложении с выделенными главными и зависимыми элементами. Обычно ровно один узел графа в подавляющем большинстве моделей, соответствующий сказуемому, не имеет подчиняющего узла и называется вершиной. Иногда двумя вершинами представляют подлежащее и сказуемое.

Отношение подчинения задает частичный порядок на множестве узлов. Если одному узлу подчиняется сразу несколько узлов , то среди последних порядок не определен: граф зависимостей не передает информацию об относительной степени близости подчиненного слова к главному. Например, граф зависимостей для фразы «программное обеспечение вычислительной техники и автоматизированных систем » (рис.9.1).

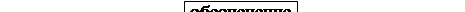
Рисунок 9.1 - Граф зависимостей

Как правило, отношение подчинения подразделяется на ряд типов, и дуги графа помечаются индексами синтаксических отношений.

Иногда граф зависимостей одновременно с отношением подчинения задает и отношение линейного порядка следования узлов. Такой граф называется расположенным. Один из способов изображения такого графа представлен на рисунке 9.2.

Рисунок 9.2 - Расположенный граф зависимостей

В большинстве случаев отношение подчинения и отношение линейного порядка слов в предложении связаны законом проективности, который при данном способе изображения формулируется так: никакая дуга, исходящая из некоторого узла, не пересекает других дуг или перпендикуляров, опущенных из более верхних узлов.

Рассмотрим расположение графа в предложениях с подчиненной и сочиненной связью. Изображение всех связей однородных членов между собой, с подчиняющими и подчиненными элементами приводит к возникновению замкнутых контуров в графах зависимостей. Чтобы избежать этого, часто используют представление, при котором сочинительная связь включается в граф зависимостей наравне с другими синтаксическими отношениями, а подчинительные связи, общие для группы однородных членов, изображаются лишь для одного члена группы (рис.9.3).

Рисунок 9.3 - Представление однородности

Пусть х — произвольная непустая цепочка и Х — множество всех точек х. Произвольное бинарное отношение ® на X, при котором граф <Х, ®> является деревом, называют отношением зависимости (подчинения). Само дерево <Х, ®> называют деревом зависимостей для х. Будем изображать дерево зависимостей цепочки ω в виде последовательности обра­зующих ее точек, расставленных на прямой линии. Для всякой пары точек а,b цепочки ω, для которой а®b, на рисунке бу­дем проводить дугу из а в b, причем таким образом, чтобы все дуги были по одну сторону от прямой. Если a ® b, то будем называть точку а управляющей точкой («хозяином»), а b—под­чиненной точкой («слугой»). На рисунке 9.4 приведены два различ­ных дерева зависимостей для цепочки agbacdef.

При анализе предложений русского языка обычно использу­ют размеченные деревья зависимостей. Размеченное дерево за­висимостей для цепочки х — это четверка <Х, ®,Z, ψ>, где <Х, ®>—дерево зависи­мостей для х; Z — конечное множество, элементы которо­го называют метками, и ψ — отображение множества дуг дерева <Х, ®> в Z.

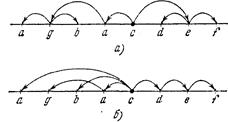
Рисунок 9.4 - Деревья зависимостей для цепочки agbacdef

Привлекательными свойствами графа зависимостей является их экономичность, удобство использования в преобразованиях, возможность представления частичных результатов анализа в виде множества подграфов.