Полную взаимозаменяемость

Чтобы обеспечить полную взаимозаменяемость, размерные цепи рассчитывают методом максимума-минимума, при котором допуск замыкающего размера определяют арифметическим сложением допусков составляющих размеров. Метод расчета на максимум-минимум, учитывающий только предельные отклонения звеньев размерной цепи и самые неблагоприятные их сочетания, обеспечивает заданную точность сборки без подгонки (подбора) деталей.

Обратная задача. Для вывода уравнений размера, предельных размеров, предельных отклонений и допуска замыкающего звена воспользуемся примером линейной размерной цепи, приведенной на рис. 2.63.

Рис. 2.63. Линейная размерная цепь

Искомые значения для замыкающего звена определятся выражениями: размер А_D = А₁ – А₂; (2.6)

предельные размеры А_D^max = A₁^max – A₂^min , А_D^min = A₁^min – A₂^max; (2.7)

предельные отклонения Еs(A_D) = Es(A₁) – Ei(A₂), Еi(A_D) = Ei(A₁)–Es(A₂); (2.8)

допуск ТА_D = ТА₁ + ТА₂. (2.9)

По аналогии с уравнениями (2.6) – (2.9) зависимости для замыкающего звена при линейной размерной цепи можно представить в общем виде:

размер 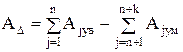; (2.10)

предельные размеры ;

;

(2.11)

предельные отклонения ;

;

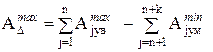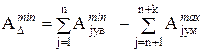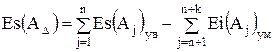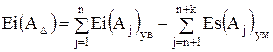допуск 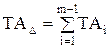, (2.12)

где n – количество увеличивающих звеньев; k – количество уменьшающих звеньев; m – общее количество звеньв, включая замыкающее звено; Es – верхнее отклонение звена; Ei – нижнее отклонение звена.

Прямая задача. Такая задача встречается на практике чаще. После определения размеров составляющих звеньев в результате конструирования механизма необходимо рассчитать допуски на эти размеры при заданной точности сборки (заданном допуске исходного размера). Точность составляющих размеров должна быть такой, чтобы гарантировалась заданная точность исходного (функционального) размера. Эту задачу можно решать одним из рассмотренных далее способов.

Способ равных допусков применяют, если составляющие размеры имеют один порядок (например, входят в один интервал диаметров) и могут быть выполнены с примерно одинаковой экономической точностью. В этом случае из формулы (2.12) получим средний допуск на звено

Т_сА_i = TA_D/(m-1).

Этот допуск корректируют для некоторых составляющих размеров в зависимости от их значений, конструктивных требований и технологических возможностей изготовления, но так, чтобы выполнялись условия по уравнениям (2.11) и (2.12). При этом выбирают стандартные поля допусков, желательно предпочтительного применения.

Способ равных допусков прост, но недостаточно точен, так как корректировка допусков составляющих размеров произвольна. Его можно рекомендовать только для предварительного назначения допусков составляющих размеров.

Способ допусков одного квалитета применяют, если все составляющие цепь размеры могут быть выполнены с допуском одного квалитета и допуски составляющих размеров зависят от их номинального значения.

Требуемый квалитет определяют следующим образом.

Допуск составляющего размера

ТА_i = а_i×i_i , (2.13)

где i — единица допуска (мкм); а — число единиц допуска, содержащееся в допуске данного размера (определяется по ГОСТу 25346 - 89).

Для размеров от 1 до 500 мм 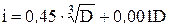, где D — средний геометрический размер (мм) для интервала диаметров по ГОСТу 25346 - 89, к которому относится данный линейный размер.

Подставив выражение (2.13) в уравнение (2.12) и решив его относительно а, получим: 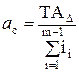. (2.14)

По значению а_с выбирают ближайший квалитет. Число единиц допуска а_с, вычисленное по формуле (2.14), в общем случае не равно како-

му-либо значению а, определяющему квалитет, поэтому выбирают ближайший квалитет. Найдя по ГОСТу 25346 - 92 или по ГОСТу 25347 – 82* допуски составляющих размеров, корректируют их значения, учитывая конструктивно-эксплуатационные требования и возможность применения процесса изготовления, экономическая точность которого близка к требуемой точности размеров. Допуски для охватывающих размеров рекомендуется определять, как для основного отверстия, а для охватываемых — как для основного вала. При этом следует удовлетворить уравнению (2.12).

Найдя допуски, определяют значения и знаки верхних и нижних отклонений составляющих размеров так, чтобы они удовлетворяли уравнениям (2.11).

Решение прямой задачи способом назначения допусков одного квалитета более обосновано, чем решение способом равных допусков.

Пример 1.Рассчитать допуски и предельные отклонения для размеров А₁, А₃, А₄

и А₆ (рис. 2.64) при заданном А_D = 1…3,5 мм.

Решим эту задачу методом полной взаимозаменяемости способом одного квалитета.

Согласно уравнению размерной цепи (2.10) A_D = A₂ + A₃ + A₄ + A₅ + A₆ - A₁ = (25 + 50 + 107 + 21 + 40) – 240 = 3.

Определяем число единиц допуска или коэффициент квалитета. Для этого используем уравнение (2.14):

,

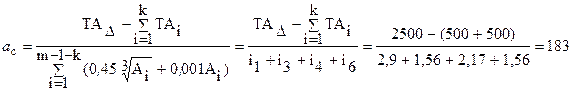где i_Ai приняли по табл.3.3 [10]; k – количество звеньев с заданными допусками.

Зная число единиц допуска а_с, по ГОСТу 25347 – 82* определяем номер квалитета. В рассматриваемом случае значение находится между IТ12 (а= 160) и IТ13 (а = 250).

Рекомендуется выбирать допуски по более грубому квалитету. Однако в нашем случае а_с ближе к IТ12, поэтому допуски на размер корпуса А₁ устанавливаем по IТ13, а на остальные (более технологичные в изготовлении размеры) – по IТ12.

Исходя из номинальных размеров звеньев цепи и выбранных квалитетов, по ГОСТу 25347-82^* определяем допуски составляющих звеньев: ТА₁ = 720 мкм; ТА₃ = 250 мкм; ТА₄ = 350 мкм; ТА₆ = 250 мкм.

Произведем проверку суммы установленных допусков составляющих звеньев с остатком допуска замыкающего звена, который должен распределиться на оставшиеся составляющие звенья:

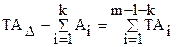. 1500 ¹ 720 + 250 + 350 + 250 = 1570.

Корректируем допуск одного составляющего звена так, чтобы получилось равенство допусков. Так как необходимо уменьшить допуск одного из звеньев, по конструкции узла следует проанализировать, какой размер экономически выгоднее выполнить более точным. Принимаем, что наиболее технологичны размеры А₃ и А₄.

Выбираем для корректировки размер А₄ и уменьшаем допуск на его изготовление на 70 мкм: ТА₄ = 280 мкм. В этом случае равенство допусков соблюдено.

Назначаем отклонения для всех составляющих звеньев.

В рассматриваемом примере на все размеры назначаем отклонения в минус, за исключением размеров А₁ и А₆, для которых отклонения назначаем симметрично.

Проставляем отклонения на размеры: A₁ = 240 ± 0,360; A₂ = 50 _{- 0,250};

A₄ = 107_{- 0,280}; A₆ = 40 ± 0,125.

Производим проверку отклонений составляющих звеньев по отклонениям замыкающего звена: E_SA_D= A_Dmax - A_D = 3,5 – 3 = + 0,5; E_iA_D = A_Dmin - A_D = 1 – 3 = -2,0;

.

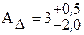Проверяем соответствие отклонений по уравнениям (2.11):

+0,5 = (0 + 0 + 0 + 0 + 0,125) – (-0,360) = 0,125 + 0,360.

Поставленное условие не удовлетворяется. Тогда принимаем неизвестными отклонения для того звена, у которого корректировали допуск (нестандартный допуск), т.е. .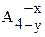

Это звено увеличивающее, значит из уравнения (2.11) определяется его верхнее отклонение: + 0,5 – 0,125 – 0,360 = x; x = + 0,015.

Зная верхнее отклонение и допуск, определим нижнее отклонение по формуле

ei = + es – T; откуда y = 0,015 – 0,280 = -0,265; .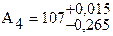

Проверим второе отклонение по формуле (2.11):

-2,0 = (-0,250) + (-0,5)×2 + (-0,265)+ (-0,125) – (+0,360) = - 2,0.

Равенство удовлетворяется, значит все допуски и отклонения составляющих звеньев определены правильно.