Теоретико-вероятностный метод расчета размерных цепей

При расчете раз­мерных цепей методом максимума — минимума предполагалось, что в процессе обработки или сборки возможно одновременное сочетание наибольших увеличивающих и наименьших уменьшающих размеров или обратное их сочетание. Оба случая наихудшие в смысле получения точности замыкающего звена, но они маловероятны, так как отклонения размеров в основном группируются около середины поля допуска. На этом положении и основан теоретико-вероятностный метод расчета размерных цепей.

Применение теории вероятностей позволяет расширить допуски составляющих размеров и тем самым облегчить изготовление деталей при практически ничтожном риске несоблюдения предельных значений замыкающего размера.

Обратная задача. В результате совместного влияния систематических и случайных погрешностей центр группирования может не совпадать с серединой поля допуска, а зона рассеяния — с величиной допуска. Величина такого несовпадения, выраженная в долях половины допуска на размер, называется коэффициентом асимметрии, ,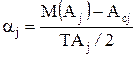

где М(А_i) – математическое ожидание, средний арифметический размер i – го звена; A_сi – размер, соответствующий середине поля допуска.

В этом случае уравнение размерной цепи по средним размерам будет иметь вид

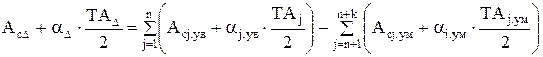. (2.15)

Используя теорему о дисперсии [D(x_i) =s_i²] суммы независимых случайных величин, можно записать: 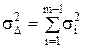. (2.16)

Для перехода от средних квадратических отклонений s к допускам или полям рассеяния используют коэффициенты относительного рассеяния l_i. Он является относительным средним квадратическим отклонением и равен (при поле рассеяния w_j = T_j)

l_j = 2s_j/T_j . (2.17)

Для закона нормального распределения (при T_j = 6s_j ) ;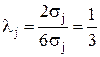

для закона равной вероятности (при ) ;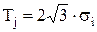

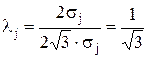для закона треугольника (Симпсона) (при ) .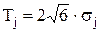

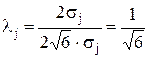Подставив выражение (2.17) в уравнение (2.16), получим:

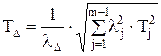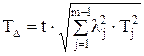или , (2.18)

где t – коэффициент, зависящий от процента риска и принимаемый по данным [10].

Определив ТА_D по формуле (2.18), вычисляют среднее отклонение замыкающего звена как Е_с(А_D) = 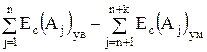(2.19)

и его предельные отклонения:

Еs(А_D) = Е_с(А_D) + TA_D/2; Еi(А_D) = Е_с(А_D) - TA_D/2. (2.20)

Прямая задача. Допуски составляющих размеров цепи при заданном допуске исходного размера можно рассчитывать четырьмя способами.

При способе равных допусков принимают, что величины ТА_j, E_c(A_j) и l_j для всех составляющих размеров одинаковы. По заданному допуску TA_D по формуле (2.18) определяют средние допуски T_cA_j:

.

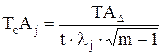Найденные значения T_cA_j и E_c(A_j) корректируют, учитывая требования конструкции и возможность применения процессов изготовления деталей, экономическая точность которых близка к требуемой точности размеров. Правильность решения задачи проверяют по формуле (2.18).

При способе назначения допусков одного квалитета расчет в общем аналогичен решению прямой задачи методом полной взаимозаменяемости. При этом среднее количество единиц допуска определится по формуле .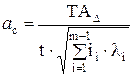

Способ пробных расчетов [50] заключается в том, что допуски на составляющие размеры назначают экономически целесообразными для условий предстоящего вида производства с учетом конструктивных требований, опыта эксплуатации имеющихся подобных механизмов и проверенных для данного производства значений коэффициентов l. Правильность расчета проверяют по формуле (2.18).

Способ равного влияния [50]применяют при решении плоских и пространственных размерных цепей. Он основан на том, что допускаемое отклонение каждого составляющего размера должно вызывать одинаковое изменение исходного размера.

Пример 2.Рассчитать допуски и предельные отклонения для размеров А₁, А₃, А₄

и А₆ (см. рис. 2.64) при заданном А_D = 1…2,12 мм. ТА_D = 1,12 мм.

Воспользуемся способом одного квалитета. Расчет ведется в той же последовательности, что и в примере 1.

Определяем коэффициент квалитета как

; ,

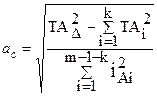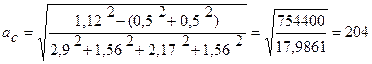где i_Ai приняли по табл.3.3 [10]; k – количество звеньев с заданными допусками.

По ГОСТу 25347 – 82* определяем, что значение а_С, равное 204, находится между по IT12 = 160 и IT13 = 250. По этому же стандарту определяем допуски на все размеры по IT12: ТА₁ = 0,460; TA₃ = 0,250; TA₄ = 0,350; TA₆ = 0,250.

Определяем допуск замыкающего звена по уравнению (2.18):

,

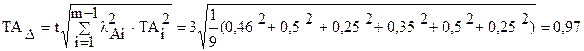где l_Аi = 1/3 - коэффициент относительного рассеяния размеров для нормального закона распределения; t = 3 – коэффициент, характеризующий процент выхода расчетных отклонений за пределы допуска, задается в зависимости от процента риска (Р = 0,27%) [10].

Условие не выполнено, т. е. 1,12 ¹ 0,97.

Чтобы получить равенство допусков, допуск одного из звеньев следует увеличить. Для этого выбираем звено А₁ (корпус) и определяем его допуск:

.

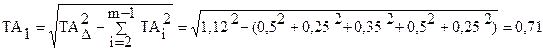Назначаем отклонения составляющих звеньев аналогично предыдущему примеру:

A₁ = 240 ± 0,355; A₂ = 25_-0,5; A₃ = 50_-0,25; A₄ = 107_-0,35; A₅ = 21_-0,5; A₆ = 40 ± 0,125.

Определяем координаты центров группирования размеров, приняв коэффициент асимметрии a_i равным нулю. Это означает, что рассеяние всех составляющих звеньев симметрично относительно середины поля допуска, и координаты центров группирования размеров будут соответствовать координатам середин полей допусков: Е_СА₁ = 0; E_CA₂ = -0,25; E_CA₃ = -0,125; E_CA₄ = -0,175; E_CA₅ = -0,25; E_CA₆ = 0.

Определяем отклонения и координаты середины поля допуска замыкающего звена: E_SA_D = A_Dmax - A_D = 2,12 – 3 = - 0,88; _iA_D = A_Dmin - A_D = 1,0 – 3 = -2,0;

E_CA_D =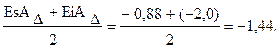

Проверяем координаты середин полей допусков по уравнению (2.19):

-1,44 ¹ [(-0,25) + (-0,125) + (-0,175) + (-0,25) + 0] – 0 = -0,8.

Для обеспечения равенства корректируем координату середины поля допуска звена А₁: E_CA₁ = -0,8 – (-1,44) = +0,64.

Определяем отклонения звена А₁:EsA₁ = E_CA₁ + ТА₁/2 = +0,64 + 0,71/2 = +0,995;

EiA₁ = E_CA₁ - ТА₁/2 = +0,64 - ,71/2 = +0,285. Звено А₁ = 240 .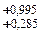

Проверка. Так как равенства в уравнениях (2.18) и (2.19) выдержаны, проверяем предельные отклонения замыкающего звена А_D по формулам (2.20):

ЕsA_D = -1,44 + 1,12/2 = - 0,88; EiA_D = -1,44 - 1,12/2 = -2,0.

Требования по замыкающему звену выдержаны.