Частные производные и дифференциалы высших порядков
Частные производные высших порядков.Пусть функция 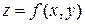 имеет непрерывные частные производные
имеет непрерывные частные производные 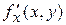 и
и 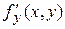 в точке
в точке 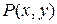
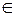 D(
D( 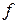 ). Эти производные, в свою очередь, являются функциями двух переменных
). Эти производные, в свою очередь, являются функциями двух переменных 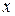 и
и 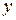 . Будем называть
. Будем называть 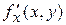 и
и 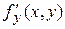 частными производными первого порядка.
частными производными первого порядка.
Частные производные по 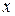 и по
и по 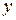 от частных производных первого порядка, если они существуют, называются частными производными второго порядкаот функции
от частных производных первого порядка, если они существуют, называются частными производными второго порядкаот функции 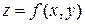 в точке
в точке 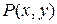 и обозначаются
и обозначаются
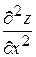 ,
, 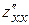 ,
, 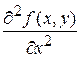 ,
, 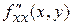
(если 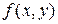 дифференцируется последовательно два раза по
дифференцируется последовательно два раза по 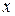 );
);
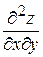 ,
, 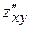 ,
, 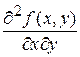 ,
, 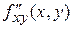
(если 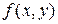 дифференцируется сначала по
дифференцируется сначала по 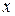 , а затем по
, а затем по 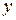 );
);
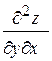 ,
, 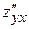 ,
, 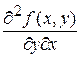 ,
, 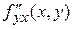
(если 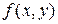 дифференцируется сначала по
дифференцируется сначала по 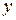 , а затем по
, а затем по 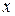 );
);
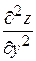 ,
, 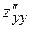 ,
, 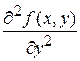 ,
, 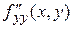
(если 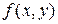 дифференцируется последовательно два раза по
дифференцируется последовательно два раза по 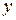 ).
).
Производные второго порядка можно снова дифференцировать как по 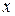 , так и по
, так и по 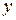 . В результате получим восемь частных производных третьего порядка:
. В результате получим восемь частных производных третьего порядка:
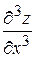 ,
, 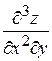 ,
, 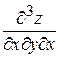 ,
, 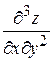 ,
, 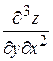 ,
, 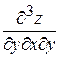 ,
, 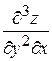 ,
, 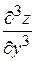 .
.
Аналогично, частная производная от производной 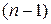 -го порядка называется частной производной
-го порядка называется частной производной 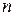 -го порядкаи обозначается
-го порядкаи обозначается
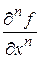 ,
, 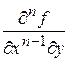 ,
, 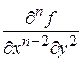 и т. д.
и т. д.
Частные производные высших порядков функции 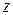 , взятые по различным переменным, например,
, взятые по различным переменным, например, 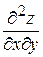 ,
, 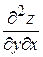 ,
, 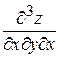 ,
, 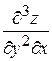 и т.д., называются смешанными производными.
и т.д., называются смешанными производными.
Среди частных производных второго порядка функции 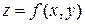 имеются две смешанные производные
имеются две смешанные производные 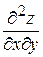 и
и 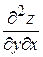 .
.
Возникает вопрос: зависит ли результат дифференцирования функций нескольких переменных от порядка дифференцирования по разным переменным.
Справедлива следующая
Теорема.Если функция 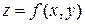 и ее частные производные
и ее частные производные 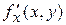 ,
, 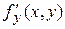 ,
, 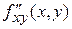 и
и 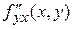 определены и непрерывны в точке
определены и непрерывны в точке 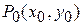 и в некоторой ее окрестности, то
и в некоторой ее окрестности, то 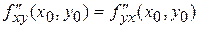 .
.
Замечание. Данная теорема, а также все приведенные выше рассуждения имеют место и для функции любого числа переменных.
Пример.Найти частные производные второго порядка функции
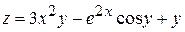 .
.
Решение. Функция определена и непрерывна на R2 . Найдем частные производные первого порядка
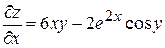 ,
, 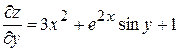 .
.
Они определены и непрерывны на R2. Найдем частные производные второго порядка
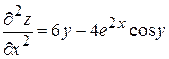 ,
, 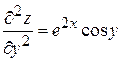 ,
,
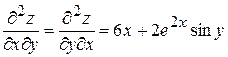 .
.
Дифференциалы высших порядков.Пусть 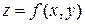 — функция двух независимых переменных
— функция двух независимых переменных 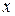 и
и 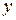 , дифференцируемая в области D(
, дифференцируемая в области D( 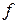 ). Придавая
). Придавая 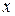 и
и 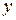 приращения
приращения 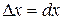 ,
, 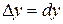 , в любой точке
, в любой точке 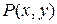
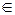 D
D 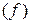 можно найти полный дифференциал
можно найти полный дифференциал
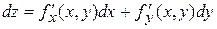 ,
,
который называют дифференциалом первого порядка функции 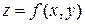 .
.
Дифференциал от дифференциала первого порядка в любой точке 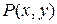
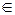 D
D 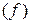 , если он существует, называется дифференциалом второго порядка и обозначается
, если он существует, называется дифференциалом второго порядка и обозначается
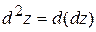 .
.
Найдем аналитическое выражение для 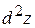 , считая
, считая 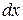 и
и 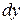 постоянными:
постоянными:
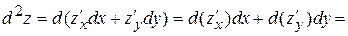
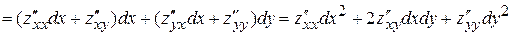 .
.
Поступая аналогично, получаем аналитическое выражение для дифференциала третьего порядка 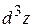 :
:
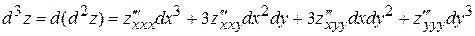 .
.
Замечание. Приведенные выше формулы дифференциалов не обладают свойствами инвариантности для сложных функций.
Пример.Найти 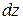 и
и 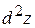 , если
, если 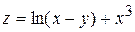 .
.
Решение. Используем формулу для вычисления полного дифференциала 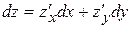 .
.
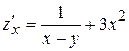 ,
, 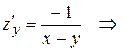
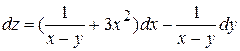 .
.
Для определения 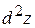 вычислим предварительно частные производные второго порядка:
вычислим предварительно частные производные второго порядка:
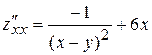 ,
, 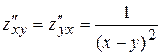 ,
, 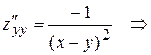
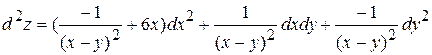 .
.
Дата добавления: 2021-01-11; просмотров: 543;











