Чисельні методи рішення систем диференціальних рівнянь на ЦОМ

Практично всі завдання, що виникають при моделюванні електроприводів, зводяться до рішення систем нелінійних ДР. Математичний апарат для аналітичного рішення таких завдань або занадто громіздкий, або відсутній. У цих умовах єдиним виходом є застосування чисельних методів інтегрування СДР.

Рішення систем нелінійних диференціальних рівнянь полягає у відшуканні залежностей Y_i(t) при відомих початкових умовах t = t₀ (початковий час) і Y_i0 = Y(t₀) (початкові значення змінних системи).

Всі відомі чисельні методи рішення систем диференціальних рівнянь діляться на два класи - однокрокові й багатокрокові. Реалізація однокрокових методів полягає в розкладанні шуканої функції в ряд Тейлора, у якого втримується те або інше число членів, що визначає порядок методу N. При однокрокових методах рішення кожне нове значення Y_j+1 знаходиться по одному відомому попередньому значенню Y_j. Як приклад реалізації однокрокового методу приведемо найпростіший метод Ейлера (першого порядку)

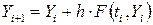
де h - крок інтегрування.

Сутність даного методу складається в заміні інтегральної кривої на кожному кроці інтегрування відрізком прямій.

Більше складним, але й більше точним є метод Рунге -Кутта 4-го порядку, що задається наступними формулами:

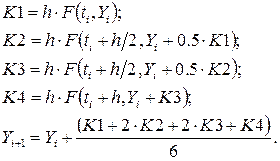
Таким чином, при використанні методу Рунге-Кутта 4-го порядку необхідно робити чотири обчислення правих частин системи диференціальних рівнянь. Тому час обчислень по цьому методі істотно зростає, хоча точність останнього істотно вище.

Однокроковим методам притаманна властивість "самостартування", а також є порівняно проста можливість зміни кроку інтегрування в процесі обчислень.

Реалізація багатокрокових методів полягає в тому, що в їх по ряду попередніх значень Y(t) с точністю екстраполяційного полінома Лагранжа обчислюється певне значення функції. Залежно від числа використовуваних попередніх значень визначається й порядок методу. До даної групи методів відносяться: група методів Адамса, метод Мілна, метод Хеммінга, група методів прогнозу й корекції.

Реалізація методу Адамса другого порядку має вигляд

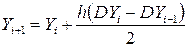
Реалізація методу Адамса четвертого порядку має вигляд

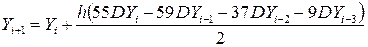
Важливим достоїнством багатокрокових методів є той факт, що для обчислення чергового значення інтегральної кривої потрібно тільки одне обчислення правих частин системи диференціальних рівнянь, що помітно прискорює рахунок. Однак цей метод не має змоги "самостартування" через відсутність попередніх значень. Для відшукання цих значень і запуску процедури багатокрокового методу необхідно використати один з наявних однокрокових методів.