Попередній аналіз задачі й способи приведення рівнянь до виду, зручному для рішення на АОМ

Математичний опис великого класу задач, пов'язаних з технікою автоматичного керування, виконується за допомогою диференціальних рівнянь (це динамічні властивості об'єктів керування, перехідні процеси й ін.)

Рівняння, розв'язувані на АОМ, є математичною моделлю вихідних (фізичних) процесів.

В АОМ принципово можливі два методи інтегрування диференціальних рівнянь:

1 - використання пристроїв, що диференціюють,

2 - метод зниження похідній.

1 -й метод практично не застосовується через посилення перешкод пристроями, що диференціюють. Розглянемо метод зниження порядку похідній на прикладі рішення диференціального рівняння 2-го порядки з постійними коефіцієнтами:

А₂Х" + А₁Х' + A₀X = у,

де А₁ A₂, А₀ - постійні числа більше 0;

у - постійне число або функція часу, тобто у= f(t) - функція, що змушує.

Вирішимо рівняння щодо вищої похідної:

де ; ;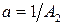

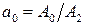Таким чином, друга похідна дорівнює сумі всіх інших членів рівняння.

АОМ складається з комплексу операційних блоків, з'єднавши які певним чином, можна одержить рішення завдання. Тому основна мова програмування завдань на АОМ - схемний спосіб.

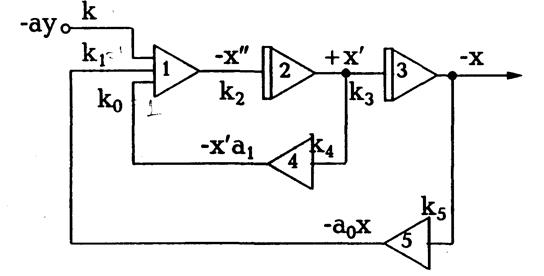
Представимо рішення диференціального рівняння у вигляді схеми, зібраної на АОМ.

Схема дає загальне уявлення про зв'язки між окремими блоками АОМ і використовується для попередньої оцінки можливості рішення підготовленого рівняння на АОМ.

При побудові схеми необхідно дотримуватися правила руху інформації ліворуч - праворуч, і зверху - долілиць.

Переходячи від схеми рішення до схеми моделювання, слід зазначити, що операція множення безперервної величини на постійне число здійснюється вирішальним підсилювачем шляхом відповідного підбора елементів вхідного ланцюга й ланцюгу зворотного зв'язка (коефіцієнта передачі К). Схема моделювання складається з вирішальних підсилювачів: підсумовуючого, інтегруючого, і інверторів.