Форми подання динамічних об'єктів

Етапи математичного моделювання

I. Розробка математичної моделі об'єкта.

Цей етап є найбільш складним, трудомістким і відповідальним. На підставі теоретичних знань, емпіричних і інтуїтивних підходів складаються математичні рівняння, що враховують найбільш важливі й істотні, з погляду дослідника, властивості об'єкта. При розробці математичної моделі необхідно уникати невиправданого ускладнення моделі, відкидати несуттєві взаємозв'язки між характеристиками об'єкта. Як приклад розглянемо математичну модель АД. Рівняння механічної характеристики по формулі Клосса також є математичною моделлю АД, тому що відбиває одне з істотних властивостей двигуна. Однак якщо необхідно точно знати механічну характеристику в діапазоні ковзань 0 < s < 1 , те ця модель буде незадовільної, тому що не враховує таких властивостей об'єкта, як насичення сталі й витиснення струму при пуску. У той же час якщо діапазон ковзань обмежений критичною точкою й точкою холостого ходу, те така математична модель буде цілком задовільною.

Таким чином, при розробці математичної моделі необхідно чітко, у явному виді, указати, які прийняти допущення при складанні рівнянь і накладаються ограничения, що, на область застосування моделі.

II. Одержання рішень математичної моделі

За допомогою складених рівнянь математичної моделі, що задаються конкретними фізичними параметрами, відшукують рішення рівнянь або аналітично, або чисельно. Для складних моделей рішення відшукують за допомогою ЕОМ. Цей етап припускає розробку структурних схем для АОМ або програми для ЦОМ і їхнє налагодження.

III. Оцінка адекватності отриманих результатів.

Після одержання рішення на математичній моделі необхідно оцінити отримані результати з погляду відповідності основним фізичним законам: закону збереження енергії, законам Кирхгофа, і ін., і просто здоровому глузду.

Форми подання динамічних об'єктів

Основною, найбільш природною формою представлення динамічного об'єкта є використання диференціальних рівнянь (ДР) або систем таких рівнянь.

,

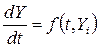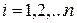
ДР, що представляють об'єкт, можуть бути лінійними й нелінійними. Інша форма подання динамічних об'єктів - у вигляді передаточних функцій по Лапласові й структурним схемам, у яких з'єднані елементарні ланки: аперіодичні, коливальні, чистого запізнювання й ін. Структурні схеми також можуть містити нелінійні елементи, математичні операції. Практично це еквівалентні форми подання динамічних об'єктів. Між цими формами існує тісний взаємозв'язок. Вони істотно розрізняються тільки по методах одержання рішення. Розглянемо як приклад аперіодичну ланку.

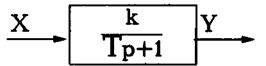
Вона має передаточну функцію виду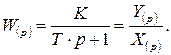

Перетворюючи це вираження, одержимо: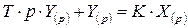

При переході з області зображень в область оригіналів остаточно одержимо: 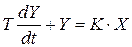, або в канонічній формі: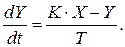

Розділ 2.