Закон распределения переходов XOR таблицы случайной подстановки.
Результаты вычислительных экспериментов по исследованию дифференциальных свойств случайных таблиц подстановок, представленные в работах [43, 172 и др.] свидетельствуют о том, что среднее значение максимумов таблиц XOR разностей случайных таблиц подстановок является специфическим показателем S-блоков фиксированной степени, не зависящим от циклового класса, к которому принадлежат подстановки.
В этом разделе выводятся расчетные соотношения для определения средних значений максимумов XOR таблиц случайных подстановок с m битным входом и m битным выходом.
Отметим сразу, что решение близкой по постановке задачи нам удалось найти в работе Luka O’Connor-а [173] 1994-го года. Однако манера представления материала Luka O’Connor-ом, особенно в части выполнения доказательств и интерпретации конечных результатов, нас не удовлетворила и сделала целесообразным изложение собственной позиции по этому вопросу [172].
Следуя работе [173], положим, что 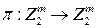 является биективным
является биективным
m-битным отображением, и пусть 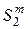 будет множеством всех таких отображений, известным в математической литературе как симметрическая группа. Пусть
будет множеством всех таких отображений, известным в математической литературе как симметрическая группа. Пусть 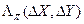 будет значением XOR таблицы (её ячейки) для пары значений разностей входов и выходов
будет значением XOR таблицы (её ячейки) для пары значений разностей входов и выходов 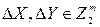 ,
, 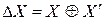 ,
, 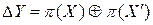 подстановки
подстановки 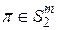 .
.
Напомним, что XOR таблица представляет собой 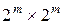 матрицу, у которой
матрицу, у которой 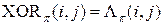 ,
, 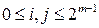 .
.
Для m-битной подстановки π XOR таблица имеет следующую общую форму

Мы будем интересоваться свойствами 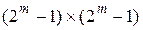 подматрицы
подматрицы 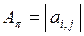 ,
, 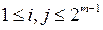 , которая соответствует части XOR таблицы с входами (ячейками), приписываемыми к ненулевым характеристикам.
, которая соответствует части XOR таблицы с входами (ячейками), приписываемыми к ненулевым характеристикам.
Рассмотрим задачу определения вероятности события, заключающегося в том, что значение дифференциальной таблицы случайно взятой подстановки π степени 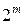 для перехода входной разности
для перехода входной разности 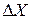 в соответствующую выходную разность
в соответствующую выходную разность 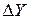 будет равно 2k (значения ячеек XOR таблицы всегда четное). Как и в [173] эту вероятность обозначим
будет равно 2k (значения ячеек XOR таблицы всегда четное). Как и в [173] эту вероятность обозначим 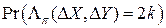 .
.
В [173] приводится теорема 2.1, определяющая эту вероятность, в виде:
Утверждение 1.Для любых ненулевых фиксированных 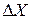 ,
,  в предположении, что подстановка π выбрана равновероятно из множества
в предположении, что подстановка π выбрана равновероятно из множества 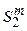 и
и 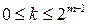 ,
,
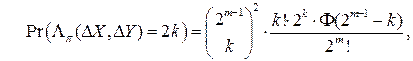 (1.2)
(1.2)
где функция 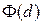 определяется выражением
определяется выражением
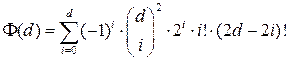 . (1.3)
. (1.3)
Как уже отмечалось выше, в [173] доказательства этих результатов приведены схематично (не полностью) и трудно понимаемы, а главное они не приведены к нужному нам виду. В работе [43] предлагается более простая и более прозрачная версия доказательства этой и других теорем с последующей оригинальной интерпретацией результатов. Мы здесь приведём её.
Д о к а з a т е л ь с т в о. Заметим сначала, что при операции вычисления разностей XOR входов подстановки π они попарно переходят друг в друга 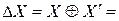
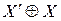 ). Поэтому в дифференциальной таблице число переходов входной разности
). Поэтому в дифференциальной таблице число переходов входной разности 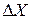 в выходную разность
в выходную разность 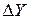 (значение ячейки таблицы дифференциальных разностей) всегда четное, и к тому же входы (и соответствующие выходы) подстановки распределяются по парам, так что для одной и той же разности
(значение ячейки таблицы дифференциальных разностей) всегда четное, и к тому же входы (и соответствующие выходы) подстановки распределяются по парам, так что для одной и той же разности 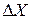 мы имеем дело с
мы имеем дело с 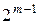 -ой парами входов. Одновременно становится понятным, что для заданного сочетания входов и выходов подстановки π каждое конкретное значение входной разности может переходить не во все возможные значения выходных разностей, и что разные пары входов с одной и той же разностью
-ой парами входов. Одновременно становится понятным, что для заданного сочетания входов и выходов подстановки π каждое конкретное значение входной разности может переходить не во все возможные значения выходных разностей, и что разные пары входов с одной и той же разностью 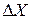 могут переходить в одну и ту же выходную разность
могут переходить в одну и ту же выходную разность 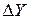 .
.
Для подстановок, выбираемых равновероятно из множества 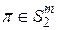 , под искомой вероятностью, очевидно, следует понимать отношение числа подстановок
, под искомой вероятностью, очевидно, следует понимать отношение числа подстановок 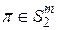 , обладающих желаемым свойством (реализующих необходимое число (2k) раз заданный переход
, обладающих желаемым свойством (реализующих необходимое число (2k) раз заданный переход 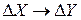 ), к общему числу подстановок симметрической группы
), к общему числу подстановок симметрической группы 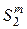 :
:
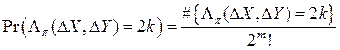 , (1.4)
, (1.4)
Выполним подсчет числа подстановок 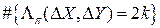 с обусловленным количеством переходов входных разностей
с обусловленным количеством переходов входных разностей 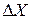 в выходную разность
в выходную разность 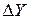 . Очевидно, что в это число будут входить подстановки, отличающиеся конфигурациями (сочетаниями) входов и выходов, участвующих в реализации желаемого свойства (реализующих необходимое число (2k) раз заданный переход
. Очевидно, что в это число будут входить подстановки, отличающиеся конфигурациями (сочетаниями) входов и выходов, участвующих в реализации желаемого свойства (реализующих необходимое число (2k) раз заданный переход 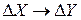 ).
).
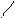 Поскольку k пар переходов любой подстановки, участвующих в реализации необходимого свойства
Поскольку k пар переходов любой подстановки, участвующих в реализации необходимого свойства 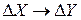 , и
, и 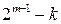 оставшихся из общего числа
оставшихся из общего числа 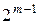 пар переходов со свойством
пар переходов со свойством 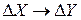 (обозначение из работы Эли Бихама и Ади Шамира [99]) компонуются в произвольном сочетании (переходы каждой из этих двух групп входов и выходов подстановки формируются независимо друг от друга), то интересующее нас число включает две компоненты (два сомножителя):
(обозначение из работы Эли Бихама и Ади Шамира [99]) компонуются в произвольном сочетании (переходы каждой из этих двух групп входов и выходов подстановки формируются независимо друг от друга), то интересующее нас число включает две компоненты (два сомножителя):
- первый сомножитель определяется числом различных подстановок π, у которых k пар входов из имеющегося в подстановке 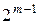 числа таких пар реализуют заданный переход
числа таких пар реализуют заданный переход 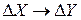 (независимо от остальных
(независимо от остальных 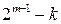 пар входов каждой из подстановок);
пар входов каждой из подстановок);
- второй сомножитель определяется дополнительным расширением множества подстановок, у которых k пар входов реализуют заданный переход 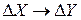 , за счет многообразия вариантов выбора
, за счет многообразия вариантов выбора 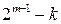 оставшихся пар входов каждой из подстановок, которые заданного перехода не реализуют, т.е. для которых
оставшихся пар входов каждой из подстановок, которые заданного перехода не реализуют, т.е. для которых 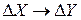 .
.
 Рассчитаем сначала число вариантов подстановок, определяющих первый сомножитель.
Рассчитаем сначала число вариантов подстановок, определяющих первый сомножитель.
Начнем с того, что в соответствии с комбинаторными соображениями для фиксированного набора из k пар входов, имеющих разность 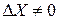 (рассматриваются входы в матрицу
(рассматриваются входы в матрицу 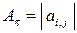 ), которые имеют заданную выходную разность
), которые имеют заданную выходную разность 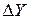 , возможно k! вариантов различных перестановок k пар выходов по заданному набору входов (подстановки нормализованного вида отличаются расстановкой пар выходных значений по парам входных).
, возможно k! вариантов различных перестановок k пар выходов по заданному набору входов (подстановки нормализованного вида отличаются расстановкой пар выходных значений по парам входных).
Очередной возможностью расширения множества подстановок, которые имеют заданное число k переходов входной разности 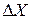 в выходную разность
в выходную разность 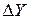 , является варьирование наборами входов и выходов подстановки, участвующими в формировании переходов входной разности
, является варьирование наборами входов и выходов подстановки, участвующими в формировании переходов входной разности 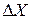 в выходную разность
в выходную разность 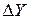 . Из общего числа
. Из общего числа 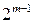 пар входов, имеющих разность
пар входов, имеющих разность 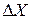 , в формировании интересующих нас переходов участвует только k пар входов. Очевидно, что они могут быть выбраны из общего числа
, в формировании интересующих нас переходов участвует только k пар входов. Очевидно, что они могут быть выбраны из общего числа 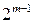 пар входов
пар входов 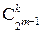 способами. Аналогичное положение характерно и для множества пар выходов, имеющих разность
способами. Аналогичное положение характерно и для множества пар выходов, имеющих разность 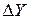 . Поскольку компоновка входных и выходных пар осуществляется независимо, то приходим к общему числу
. Поскольку компоновка входных и выходных пар осуществляется независимо, то приходим к общему числу 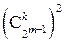 вариантов подстановок с интересующим нас свойством.
вариантов подстановок с интересующим нас свойством.
Наконец, имеется еще одна степень свободы в построении подстановок с заданным числом переходов входной разности 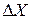 в выходную разность
в выходную разность 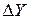 . Одна и та же пара входов с разностью
. Одна и та же пара входов с разностью 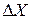 может реализовать два варианта переходов в выходную разность
может реализовать два варианта переходов в выходную разность 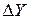 (входы подстановки, входящие в пару, можно поменять местами). Но тогда множество возможных подстановок с фиксированным переходом входной разности
(входы подстановки, входящие в пару, можно поменять местами). Но тогда множество возможных подстановок с фиксированным переходом входной разности 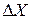 в выходную разность
в выходную разность 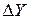 дополнительно увеличится ещё в
дополнительно увеличится ещё в  раз.
раз.
В результате мы действительно для вероятности того, что значение дифференциальной таблицы случайно взятой подстановки π степени 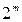 с переходом входной разности
с переходом входной разности 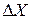 в соответствующую выходную разность
в соответствующую выходную разность 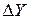 будет равно числу 2k, приходим к соотношению (1.2), в котором роль второго сомножителя, о котором шла речь выше, играет функция
будет равно числу 2k, приходим к соотношению (1.2), в котором роль второго сомножителя, о котором шла речь выше, играет функция 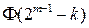 .
.
Остается учесть варианты расширения множества подстановок интересующего нас вида за счет второго сомножителя. В работе [173], чтобы определить второй сомножитель выводится расчетное соотношение для функции 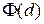 в виде соотношения (1.3).
в виде соотношения (1.3).
Для получения этого расчетного соотношения в [173] использована ²Спаривающая теорема², краткое доказательство которой без разъяснений, приводит автор. Здесь предлагается оригинальный вариант вывода расчетного соотношения для функции 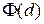 , являющегося по существу следствием доказанного выше соотношения (1.2).
, являющегося по существу следствием доказанного выше соотношения (1.2).
Будем теперь интересоваться ²хвостом² из 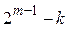 пар входов и выходов, которые в предыдущем рассмотрении не учитывались (считались фиксированными). По оговоренному условию это пары, которые не имеют заданного перехода
пар входов и выходов, которые в предыдущем рассмотрении не учитывались (считались фиксированными). По оговоренному условию это пары, которые не имеют заданного перехода 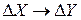 . Множество этих пар можно рассматривать как отдельную подстановку степени
. Множество этих пар можно рассматривать как отдельную подстановку степени 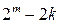 . Тогда для определения числа подстановок степени
. Тогда для определения числа подстановок степени 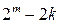 , не имеющих заданного перехода
, не имеющих заданного перехода 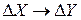 , очевидно можно просто из общего числа подстановок такой степени вычесть число подстановок, имеющих заданный переход. Подстановки степени
, очевидно можно просто из общего числа подстановок такой степени вычесть число подстановок, имеющих заданный переход. Подстановки степени 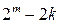 с обусловленным переходом могут содержать одну пару с таким переходом, две пары, и так до
с обусловленным переходом могут содержать одну пару с таким переходом, две пары, и так до 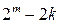 пар переходов.
пар переходов.
В результате в терминах функции 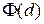 выражение для расчета второго сомножителя можно представить в виде [43]
выражение для расчета второго сомножителя можно представить в виде [43]
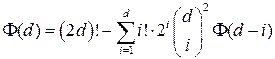 . (1.5)
. (1.5)
Остается показать, что представления (1.2) и (1.5) эквивалентны.
Это легко устанавливается последовательной подстановкой в (1.5) значений функции 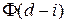 ,
,  и использованием очевидных соотношений
и использованием очевидных соотношений
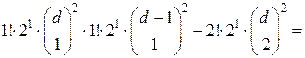
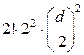
для коэффициента при функции 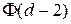 после подстановки в (3.5) явного вида функции
после подстановки в (3.5) явного вида функции 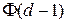 ;
;
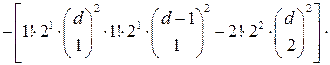
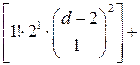
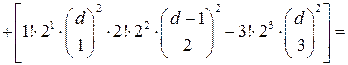
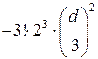
для коэффициента при функции 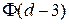 после подстановки в (1.5) явного вида функции
после подстановки в (1.5) явного вида функции 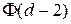 и так до свертывания коэффициентов при всех последующих функциях
и так до свертывания коэффициентов при всех последующих функциях 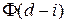 ,
, 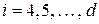 . В результате приходим к выражению (1.3). Утверждение доказано.
. В результате приходим к выражению (1.3). Утверждение доказано.
Далее, как и в [173] обозначим ожидаемое число ненулевых характеристик 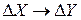 для которых
для которых 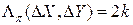 как
как 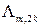 .
.
При выводе выражения (1.2) мы не фиксировали значений пары разностей, 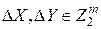 , для которых оно получено. Это значит, что соотношение (1.2), справедливо для произвольных сочетаний разностей на входе и выходе подстановок. Мы уже отмечали ранее, что результаты, полученные для ансамбля подстановок, считаются справедливыми и для отдельной подстановки π, т.е. полученные формулы можно трактовать как закон распределения ненулевых характеристик для каждой подстановки.
, для которых оно получено. Это значит, что соотношение (1.2), справедливо для произвольных сочетаний разностей на входе и выходе подстановок. Мы уже отмечали ранее, что результаты, полученные для ансамбля подстановок, считаются справедливыми и для отдельной подстановки π, т.е. полученные формулы можно трактовать как закон распределения ненулевых характеристик для каждой подстановки.
Выражение (1.2) определяет вероятность того, что в XOR таблице случайно взятой подстановке число переходов входной разности 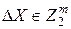 в выходную разность
в выходную разность 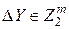 будет равно 2k.
будет равно 2k.
Но тогда становится понятным, что выражение для числа 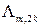 переходов таблицы дифференциальных разностей подстановки степени
переходов таблицы дифференциальных разностей подстановки степени 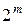 обусловленного типа, - а именно для среднего значения числа ненулевых характеристик
обусловленного типа, - а именно для среднего значения числа ненулевых характеристик 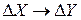 , таких, что
, таких, что 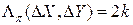 , - может быть получено путем умножения выражения (1.2) на число ячеек подматрицы
, - может быть получено путем умножения выражения (1.2) на число ячеек подматрицы 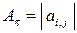 таблицы
таблицы 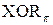 равное
равное 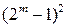 :
:
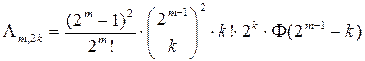 . (1.6)
. (1.6)
Это выражение и есть то, которое нам нужно.
1.3.6 Сравнение расчетных и экспериментальных результатов
Нас теперь будет интересовать среднее значение максимума таблицы XOR разностей. Оно находится из соотношения (1.6) просто путем определения максимального значения k, при котором результат расчетов по этому выражению приводит к наименьшему целому значению. Другими словами, нам нужно найти решение уравнения
 . (1.7)
. (1.7)
Это решение можно искать переборным методом, ориентируясь при этом на экспериментальные данные.
Полезной аппроксимацией для выполнения расчетов может стать и еще один результат, также приведенный в работе [173]. Имеется в виду замечание о том, что в знакопеременной сумме в выражении (1.3) первый терм (при значении 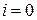 ) является доминирующим, и что
) является доминирующим, и что 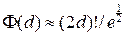 .
.
Остается заметить, что 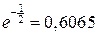 .
.
Например, для m = 4, k = 3 получим
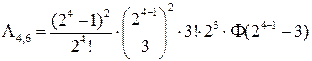 .
.
С учетом того, что  2088960 в итоге приходим к результату
2088960 в итоге приходим к результату
 .
.
Мы получили ожидаемое среднее значение максимума таблицы дифференциальных разностей для значения m = 4 несколько большее 2k = 6, что хорошо согласуется с результатами наших экспериментов.
Для других значений m расчеты, выполненные в соответствии с соотношениями (1.2), (1.3) и (1.6), представлены в таблице 1.4.
Таблица 1.4
Сравнение расчетных и экспериментальных результатов для случайных подстановок различных степеней
| n | 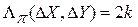
| 2k | Эксперимент |
| 3,379 0,459 | 6,7 ≤ (m + 3) | ||
| 3,08 1,708 | 7,94 ≤ (m + 3) | ||
| 6,6 0,675 | 9,1 ≤ (m + 4) | ||
| 2,641 0,221 | 10,3 ≤ (m + 4) | ||
| 10,26 0,8748 | 11,4 ≤ (m + 4) | ||
| 3,474 0,248 | 12,5 ≤ (m + 4) | ||
| 13,8495 0,99 | 13,4 ≤ (m + 4) | ||
| 3,952 0,247 | 14,5 ≤ (m + 4) | ||
| 15,787 0,987 | 15,3 ≤ (m + 4) | ||
| 15,76 0,87 | 17,6 ≤ (m + 4) | ||
| 14,01 0,7 | 19,5 ≤ (m + 4) | ||
| 8,155 0,239 | - ≤ (m + 4) |
В этой таблице также представлены результаты, полученные экспериментальным путём на основе статистической обработки множества значений максимумов дифференциальных таблиц подстановок, сгенерированных случайным образом.
Таблица 1.5 иллюстрирует результаты вычислительного эксперимента по оценке среднего значения максимумов дифференциальных таблиц случайных подстановок, приведенные в работе [43] (здесь мы их приводим в более полном объеме).
Сопоставление результатов таблиц 1.4 и 1.5 свидетельствует о хорошем согласовании экспериментальных и следующих из теоретических расчётов результатов.
Главный вывод из представленных результатов состоит в том, что средне значение максимумов дифференциальных таблиц случайных подстановок является вполне определённым значением, зависящим от степени подстановки, которое может быть получено расчётным путём.
Таблица 1.5
 Результаты вычислительного эксперимента
Результаты вычислительного эксперимента
 Степень подста-
Число новки
циклов Степень подста-
Число новки
циклов
| 23 = 8 | 24 = 16 | 25 = 32 | 26 = 64 | 27 = 128 | 28 = 256 | 29 = 512 | 210 = 1024 | 211 = 2048 | 212 = 4096 |
| 4.8014 | 6.69454 | 7.94398 | 9.11202 | 10.2827 | 11.4222 | 12.0 | 13.75 | 15.3333 | 14.0 | |
| 4.2591 | 6.71003 | 7.94526 | 9.11991 | 10.2921 | 11.3765 | 12.3467 | 13.6429 | 14.1538 | 15.0 | |
| 4.7807 | 6.68965 | 7.94006 | 9.11311 | 10.3022 | 11.4241 | 12.3697 | 13.2647 | 14.3947 | 15.68 | |
| 4.2616 | 6.71753 | 7.94177 | 9.11112 | 10.3097 | 11.3012 | 12.5144 | 13.4481 | 14.5745 | 15.3235 | |
| 4.9487 | 6.6881 | 7.94223 | 9.10677 | 10.3043 | 11.3252 | 12.4528 | 13.4565 | 14.3969 | 15.4066 | |
| 4.5187 | 6.71281 | 7.95425 | 9.11403 | 10.3178 | 11.3645 | 12.4948 | 13.3743 | 14.529 | 15.3509 | |
 7 7
| 8.0 | 6.72067 | 7.94278 | 9.11009 | 10.3157 | 11.3144 | 12.4095 | 13.4121 | 14.3967 | 15.37 |
| 8.0 | 6.84496 | 7.94878 | 9.11502 | 10.3248 | 11.3216 | 12.4316 | 13.4607 | 14.5284 | 15.4055 | |
| 7.0137 | 7.95743 | 9.11899 | 10.3165 | 11.2887 | 12.4122 | 13.3596 | 14.5089 | 15.4027 | ||
| 6.91892 | 7.98563 | 9.1015 | 10.3071 | 11.3538 | 12.5669 | 13.4009 | 14.4336 | 15.4268 | ||
| 8.0 | 8.03191 | 9.15496 | 10.3183 | 11.359 | 12.4249 | 13.3284 | 14.4715 | 15.368 | ||
| 7.6 | 9.0 | 10.2954 | 11.3429 | 12.3457 | 13.2179 | 14.4822 | 15.3313 | |||
| 8.0 | 9.42222 | 10.2264 | 11.0667 | 12.7111 | 13.55 | 14.4785 | 15.2735 | |||
| 9.0 | 10.5882 | 11.0 | 12.7619 | 13.125 | 14.3939 | 15.625 | ||||
| 10.0 | 9.33333 | 11.0 | 12.0 | 13.4667 | 14.1935 | 15.4333 | ||||
| 10.0 | 12.0 | 12.0 | 13.5 | 14.4 | 15.5333 | |||||
| 10.0 | 13.0 | 14.0 | 15.7143 | |||||||
| 14.0 | 14.05.09 | 15.6 | ||||||||

| - | 16.5 | ||||||||
| Число подстановок |

Интересно отметить, что для закона распределения (1.2), рассматриваемого над подматрицей  выполняется соотношение
выполняется соотношение
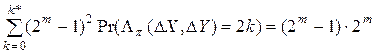
Это означает, что для выражения (3.2) с большой точностью выполняется условие нормировки
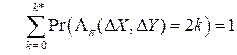 .
.
Здесь k* представляет собой половину от максимального значения числа переходов XOR таблицы случайной подстановки.
Таким образом, формула (1.2) может рассматриваться как закон распределения числа ненулевых (по входу) переходов  для отдельной подстановки, т.е. набор значений переходов
для отдельной подстановки, т.е. набор значений переходов 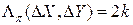 ,
, 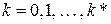 представляет практически полную группу событий. Мы фактически и воспользовались этим, выполняя вычисления по выражению (1.6).
представляет практически полную группу событий. Мы фактически и воспользовались этим, выполняя вычисления по выражению (1.6).
В таблице 1.6 представлены результаты вычисления значений ²хвостов² формулы (1.2), т.е. 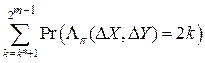 как функции размера битового входа подстановки m (в скобках представлены значения этих же сумм ²хвостов², умноженных на число ячеек подматрицы
как функции размера битового входа подстановки m (в скобках представлены значения этих же сумм ²хвостов², умноженных на число ячеек подматрицы 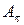 XOR таблицы). Видно, что даже в ²нормированном² варианте доля сумм ²хвостов² оказывается незначительной.
XOR таблицы). Видно, что даже в ²нормированном² варианте доля сумм ²хвостов² оказывается незначительной.
Таблица 1.6
Результаты расчетов хвостов распределений
| m | k* | 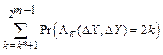
|
| 0,00245 (0,55) | ||
| 0,000015 (0,06) | ||
| 0,000001 (0,065) | ||
| 0,00000006 (0,062) | ||
| 0,0000000034 (0,0057) |
Этим подтверждается высказанная в начале подраздела установка, что свойства отдельной случайной подстановки однозначно выражаются через свойства ансамбля случайных подстановок.
1.3.7 Методика построения дифференциальных таблиц подстановочных преобразований
Вероятность перехода заданной входной разности 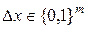 в выходную разность
в выходную разность 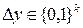 при прохождении через S-блок
при прохождении через S-блок 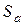 определяется следующим образом:
определяется следующим образом:
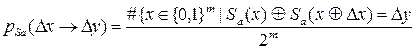 ,
,
здесь символ #{×} обозначает мощность множества в скобках; в данном случае #{×} есть число пар входов в S-блок из общего возможного их числа 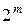 , для которых их разность
, для которых их разность 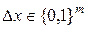 на входе S-блока переходит в разность
на входе S-блока переходит в разность 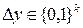 на его выходе (за чертой в скобках стоит обусловленное событие).
на его выходе (за чертой в скобках стоит обусловленное событие).
Поскольку для подстановки, которой является S-блок, не все переходы возможны, и не все возможные переходы равновероятны, то для изучения прохождения разностей через S-блоки авторы дифференциального криптоанализа предложили для каждого S-блока строить таблицу разностей, в которую заносятся значения  для всех возможных вариантов пар разностей
для всех возможных вариантов пар разностей 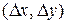 на входе и выходе S-блока
на входе и выходе S-блока 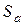 .
.
Алгоритм построения таблицы разностей таков:
1. Обнуляются все ячейки таблицы необходимой размерности (2m ´2k);
2. В цикле перебираются все возможные пары (x1Î{0,1}m, x2Î{0,1}m) значений входов в S-блок;
3. Для каждого получающегося варианта входной разности 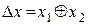 определяется выходная разность как
определяется выходная разность как 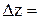
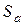 (x1)Å
(x1)Å 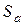 (x2);
(x2);
4. Инкрементируется значение ячейки, соответствующей рассматриваемой паре значений входов 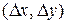 в таблицу разностей.
в таблицу разностей.
Очевидно, что нулевая разность на входе любого S-блока будет всегда переходить в нулевую разность на его выходе. Таблица позволяет оценить вероятности переходов для всех ненулевых входных разностей (при ненулевых входных разностях возможны и нулевые выходные разности). В частности, используя таблицу разностей, легко определить и максимальную вероятность прохождения ненулевой разности через S-блок
 .
.
Как мы увидим из дальнейшего, именно значения максимально достижимых вероятностей переходов S-блоков станут определяющими при оценке устойчивости шифра к атакам дифференциального криптоанализа.
Содержание заданий и исследований работы
1.4.1. Разработка программного продукта по построению таблицы дифференциальных рназностей подстановочного преобразования
Для выполнения этого пункта необходимо:
- пользуясь правилами построения таблиц диффернциальных разностей, представленными в п. 1.3.7 подготовить программную реализацию процедуры построения дифференциальной таблицы для подстановки с n-битным входом и n-битным выходом (n = 4,8,16), а также процедуры определения максимального значения XOR таблицы;
- программно реализовать генератор случайных подстановок для
значений степени n = 4,8;
- пользуясь разработанными программами построить дифференциальные таблицы для n = 4,8 и определить максимальные значения этих таблиц для случайно сгенерированных S-блоков.
- разработать пользовательский интерфейс для проведения исследования дифференциальных свойств подстановочных преобразований как случайного, так и заданного вида.
- исследовать дифференциальные свойства подстановочных преобразований степени 4 и 8.
- исследовать дифференциальные свойства произведения последовательности подстановочных преобразований.
Содержание отчёта
Отчёт должен содержать:
- цель исследований и программу исследований работы;
- разработанный вариант программного комплекса исследования дифференциальных свойств подстановочных преобразований;
- результаты экспериментальных исследований с помощью этого комплекса дифференциальных свойств случайно сгенерированных и заданных преподавателем подстановочных преобразований.
1.6 Контрольные вопросы и задания
1. Дайте определение XOR таблицы подстановки.
2. Назовите известные вам показатели случайности подстановочных преобразований.
3. Приведите определение цикла подстановки.
4. Назовите комбинаторные свойства случайных подстановок.
5. Сформулируйте особенности дифференциальных свойтв случайных подстановок.
6. Как определяется дифференциальная вероятность?
7. Изложите методику определения теоретического значения максимума дифференциальной вероятности.
8. Изложите сущность предлагаемого метода определения вероятности получения подстановки с заданным значением дифференциального перехода.
9. Сущность методики построения дифференциальной таблицы подстановки.
Литература.
131. E.F. Brickell, J.H. Moore, and M.R. Purtill. Structure in the S-boxes DES. Advances in cryptology, CRYPTOZb, Lecture Notes in Computer Science, vol. 263. A.M. Odlyzko ed., Springer-Verlag, pages 3-8, 1987.
132.С. М. Adams.A formal and practical design procedure for Substitution-Permutation network cryptosystem. PhD thesis, Department of Electrical Engineering, Queen's University at Kingston, 1990.
133. С. M. Adams. And S.E. Tavares. The Structured design of cryptographically good S-boxes. Journal of Cryptology, 3(1): 27-41, 1990.
134. R. Forré. Methods and instruments for designing S-boxes. Journal of Cryptology, 2(3): 115-130,1990.
135. K. Nyberg. Perfect nonlinear S-boxes.In Advances in cryptology -EUROCRYPT91, volume 547, Lecture Notes in Computer Science, pp. 378-386. Springer-Verlag, Berlin, Heidelberg, New York, 1991.
136. M. H. Dawson. A unified framework for substitution box design based on information theory. Vaster's thesis, Queen's University, Kingston, Ontario, Canada, 1991.
99. E. Biham and A. Shamir. Differential Cryptanalysis of DES-like Cryptosystems. Journal of Cryptology, 4(1): 3-72, 1991.
137. Matsui, M.: Linear cryptanalysis method for DES cipher. In Advances in Cryptology.- EUROCRYPT'93 (1994) vol. 765. Lecture Notes in Computer Science Springer-Verlag, Berlin, Heidelberg, New York pp. 386-397.
130. F. Sano, K. Ohkuma, H. Shimizu, S. Kawamura. On the Security of Nested SPN Cipher against the Differential and Linear Cryptanalysis/ IEICE Trans. Fundamentals, vol. E86-a, NO.1 January 2003, pp. 37-46.
138. K. Nyberg and L.R. Knudsen. Provable security against differential cryptanalysis. In Advances in cryptology - EUROCRYPT'92, volume Lecture Notes in Computer Science, Springer-Verlag, Berlin, Heidelberg, New York, 1992, pp. 566-574.
139. T. Beth and C. Ding. On permutations against differential cryptanalysis. In Advances in cryptology - EUROCRYPT'93. Springer-Verlag, Berlin, Heidelberg, New York, 1993.
140. Seberry J., Zhang X.M., Zheng Y. "Pitfalls in Designing Boxes (Extended Abstract)"//, Copyright © Springer-Verlag, 1998, pp. 383-396.
141. Seberry J., Zhang X.M., Zheng Y.: Relationships among nonlinearity criteria. Presented at EUROCRYPTV4, 1994.
142. Zhang X.M, Zheng Y, Imai. H.: Non-existence of Certain Quadratic S-boxes and Two Bounds on Nonlinear Characteristics of General S-boxes // October 1997, pp. 1-18.
143. K. Nyberg. On the construction of highly nonlinear permutations. In Advances in cryptology - Proceedings of EUROCRYPT'92 (1993) vol. 740, Lecture Notes in Computer Science Springer-Verlag, Berlin, Heidelberg, New York pp. 92-98.
144. Seberry J., Zhang X.M., Zheng Y. Improving the strict avalanche characteristics of cryptographic functions. Information Processing Letttrs, 50:37-41, 1994.
15. К. Шеннон. Теория связи в секретных системах. Работы по теории информации и кибернетики. Изд. иностр. лит., - 1963. - С. 333-402.
163. Borst. Block Ciphers: Design, Analysis and Side-Channel Analysis. PhD thesis, Dept. Elektrotechniek, Katholieke Universiteit Leuven, Belgium, Sep 2001.
164. Завало С.Т., Костарчук В.Н., Хацет Б.И. Алгебра и теория чисел. / - ч.2. - К.: Вища школа -1980. - 407 с.
165. Сачков В.Н. Введение в комбинаторные методы дискретной математики. - М.: Наука – 1982 – 384c.
166. Сачков В.Н. Комбинаторные методы дискретной математики. - М.: Наука, - 1977. - 319с.
167. Математическая энциклопедия: В 5 т. / Гл. ред. Виноградов И.М. - М.: Советская энциклопедия, 1979. - Т.2: Д-КОО. - 278 с.
168. Сачков В.Н. Вероятностные методы в комбинаторном анализе. - М.: Наука, 1978. - 285 с.
169. Риордан Дж. Введение в комбинаторный анализ: Пер с англ. - М.: ИЛ, 1963. - 287 с.
170. Райзер Г. Дж. Комбинаторная математика: Пер с англ. - М.:ИЛ, 1966. - 97
171. Бронштейн И.Н. Справочник по математике для инженеров и учащихся вузов. / И.Н. Бронштейн, К.А. Семендяев // Изд-во М:. ²Наука² 1980, 976 стр.
172. Олейников Р. В., Лисицкий К. Е. Исследование дифференциальных свойств подстановок различных цикловых классов. Двенадцатая Международная научно-практическая конференция ²Безопасность информации в информационно-телекоммуникационных системах ², 19-22 МАЯ 2009 г., Тезисы докладов. - К.: ЧП “ЕКМО”, НИЦ “ТЕЗИС” НТУУ “КПИ”, 2009. - С. 24-25.
173. L.J. O’Connor. On the Distribution of Characteristics in Bijective Mappings. Advances in Cryptology. EUROCRIPT 93, Lecture Notes in Computer Science, vol. 795, T. Helleseth ed., Springer-Verlag, pages 360-370, 1994.
174. Luke O’Connor. Properties of Linear Approximation Tables. Email: oconnor@dsts. Edu. au, 1995.
175. Luke O’Connor. On Linear Approximation Tables and Ciphers secure against Linear Cryptanalysis. Email: oconnor@dsts. Edu. au, 1995. (семь страниц).
176. Долгов В.И. Анализ циклических свойств блочных шифров. / В.И. Долгов, И.В. Лисицкая, В.И. Руженцев // Прикладная радиоэлектроника. – 2007. – Т.6, №2 – С. 257-263.
177. Nicolas T. Courtois, Gregory V. Bard, and Shaun V. Ault. Statistics of Random Permutations and the Cryptanalysis Of Periodic Block Ciphers, J. Math. Crypt. 2 (2008), 1-20.
178. Joan Daemen, Vincent Rijmen Probability distributions of Correlation and Differentials in Block Ciphers. / Joan Daemen, Vincent Rijmen // April 13, 2006, pp. 1-38.
157. Лисицкая И.В. К вопросу построения долговременных ключей для алгоритма ГОСТ-28147-89. Информационно-управляющие системы на железнодорожном транспорте. – 1997. – №3. – С. 54-57.
33. E. Biham and A. Shamir, “Differential Cryptanalysis of DES-Like Cryptosystems”, Journal of Cryptology, vol. 4, no.1, pp.3-72, 1991.
43. Олейников Р.В. Дифференциальные свойства подстановок / Р.В. Олейников, О.И. Олешко, К.Е. Лисицкий, А.Д. Тевяшев // Прикладная радиоэлектроника. - 2010. - Т.9. - № 3. - С. 326-333.
99. E. Biham and A. Shamir. Differential Cryptanalysis of DES-like Cryptosystems. Journal of Cryptology, 4(1): 3-72, 1991.
Лабораторная работа № 2
Исследование линейных свойств подстановочных преобразований
(S-блоков)
Цель работы
Освоить методику построения таблиц линейных аппроксимаций
S-блоков. Разработать программную реализацию процедур генерирования случайных S-блоков и построения таблиц линейных аппроксимаций для них.
Дата добавления: 2016-09-26; просмотров: 2167;











