Итак, возможны только те орбиты для которых

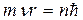. (32.17)

Число n называется главным квантовым числом.

Уравнение движение электрона в поле ядра с зарядом Z имеет вид (роль центростремительной силы выполняет сила кулоновского притяжения электрона к ядру с зарядом ):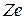

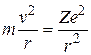. (32.18)

Выразим скорость электрона из уравнения (32.17):

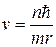(32.19)

и подставим в уравнение движения (32.18):

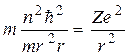(32.20)

Выразим из (32.20) радиус орбиты:

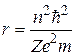(32.21)

Поскольку 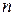- целое число(!),(32.21) означает, что в атоме реализуются только дискретные орбиты движения электрона; они и есть стационарные орбиты.

Радиус первой орбиты называется Боровским:

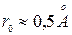
Это значение вполне согласуется с экспериментальным значением, полученным методами молекулярной физики.

Внутренняя энергия атома водорода складывается из кинетической энергии электрона и потенциальной энергии его взаимодействия с ядром:

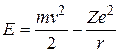(32.22)

Из уравнения движения электрона (32.18) 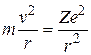следует:

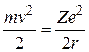(32.23)

Поэтому выражению для полной энергии (32.21) можно придать вид:

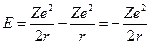(32.24)

Подставим значение радиуса орбиты из (32.21)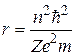

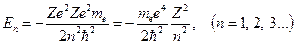(32.25)

Отсюда следует, что энергия электрона изменяется дискретно, т.е. может принимать только строго определенные значения.

В соответствии с постулатами Бора, в атоме водорода ( 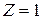) при переходе из состояния с энергией 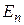в состояние с энергией 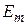должен испускаться (или поглощаться) квант электромагнитного излучения с энергией

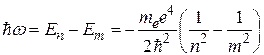(32.25)

Тогда для частоты фотона оказывается справедливо соотношение:

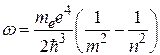(32.25)

Соотношение (32.25) представляет собой обобщенную формулу Бальмера, если положить, что постоянная Ридберга

.

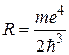Это соотношение очень точно соответствует экспериментальному, что подтверждает разумность постулатов Бора.

Тем не менее, впоследствии выяснилось, что на основе постулатов Бора хорошо объясняются свойства только атомов водорода. Все попытки построить аналогичную теорию для более сложных атомов оказались безуспешными.

Тем не менее, основные представления теории Бора во многих случаях оказываются полезными для того, чтобы представить поведение реальных атомов и объяснить их свойства, хотя инее вполне точно.