Уравнения плоской и сферической волн

Волновые процессы. Основные понятия и определения

Рассмотрим некоторую упругую среду - твёрдую, жидкую или га­зообразную. Если в каком-либо месте этой среды возбудить колебания её частиц, то вследствие взаимодействия между частицами, колебания будут, передаваясь от одной частицы среды к другой распространяться в среде с некоторой скоростью 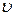. Процесс распространения колеба­ний в пространстве называется волной.

Если частицы в среде колеблются в направлении распростране­ния волны, то она называется продольной. Если колебания частиц происходят в плоскости, перпендикулярной направлению распространения волны, то волна называется попереч­ной. Поперечные механические волны могут возникнуть только в сре­де, обладающей ненулевым модулем сдвига. Поэтому в жидкой и газо­образной средах могут распространяться только продольные волны. Различие между продольными и поперечными волнами наиболее хорошо видно на примере распространения колебаний в пружине - см. рисунок.

Для характеристики поперечных колебаний необходимо задать положение в пространстве плоскости, проходящей через направление колебаний и направление распространения волны - плоскости поляризации.

Область пространства, в которой колеблются все частицы среды, называется волновым полем. Граница между волновым полем и остальным пространством среды называется фронтом волны. Иначе говоря, фронт волны - геометрическое место точек, до которых колебания дошли к данному моменту времени. В однородной и изотропной среде направление распространения волны перпендикулярно к фронту волны.

Пока в среде существует волна, частицы среды совершают колебания около своих положений равновесия. Пусть эти колебания являются гармоническими, и период этих колеба­ний равен Т . Частицы, отстоящие друг от друга на расстояние

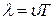(22.1)

вдоль направления распространения волны, совершают колебания одинаковым образом, т.е. в каждый дан­ный момент времени их смещения одинаковы. Расстояние 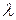называется длиной волны. Другими словами, длина волны есть расстояние, на которое распространяется волна за один период колебаний.

Геометрическое место точек, совершающих колебания в одной фазе называется волновой поверхностью. Фронт волны – частный случай волновой поверхности. Длина волны – минимальное расстояние между двумя волновыми поверхностями, в которых точки колеблются одинаковым образом, или можно сказать, что фазы их колебаний отличаются на .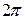

Если волновые поверхности являются плоскостями, то волна называется плоской, а если сферами – то сферической. Плоская волна возбуждается в сплошной однородной и изотропной среде при колебаниях бесконечной плоскости. Возбуждение сферической можно представить в виде результата радиальных пульсаций сферической поверхности, а также как результат действия точечного источника, размерами которого по сравнению с расстоянием до точки наблюдения можно пренебречь. Поскольку любой реальный источник имеет конечные размеры, на достаточно большом расстоянии от него волна будет близка к сферической. В то же время участок волновой поверхности сферической волны по мере уменьшения его размеров становится сколь угодно близким к участку волновой поверхности плоской волны.

Уравнения плоской и сферической волн

Уравнением волны называется выражение, которое определяет сме­щение колеблющейся точки, как функцию координат равновесного поло­жения точки и времени:

Если источник совершает периодические колебания, то функция(22.2) должна быть периодической функцией и координат и времени. Периодичность по времениследует из того, что функция 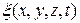описывает пе­риодические колебания точки с координатами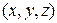; периодич­ность по координатам - из того, что точки находящиеся на расстоя­нии 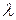вдоль направления распространения волны, колеблются одинаковым образом

Ограничимся рассмотрением гармонических волн, когда точки среды совершают гармонические колебания. Необходимо отметить, что любую негармоническую функцию можно представить в виде результата наложения гармонических волн. Поэтому рассмотрение только гармонических волн не приводит к принципиальному ухудшению общности получаемых результатов.

Рассмотрим плоскую волну. Выберем систему координат так, чтобы ось Ох совпадала с направлением распространения волны. Тогда волновые поверхности будут перпендикулярны к оси Ох и, поскольку все точки волновой поверхности ко­леблются одинаково, смещение точек среды из положений равновесия 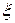будет зависеть только отх и t:

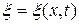(22.3)

Пусть колебания точек, лежащих в плоскости 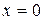имеют вид:

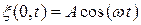(22.4)

Колебания в плоскости, находящейся на расстоянии х от начала координат, отстают по времени от колебаний в 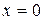на промежуток времени 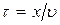, необходимый волне для преодоления расстояния х, и описываются уравнением

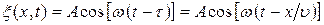, (22.5)

которое и является уравнением плоской волны, распространяющейся в направлении оси Ох.

При выводе уравнения (22.5) мы предполагали амплитуду колебаний одинаковой во всех точках. В случае плоской волны это выполняет­ся, если энергия волны не поглощается средой.

Рассмотрим некоторое значение фазы, стоящей в уравнении (22.5):

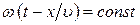(22.6)

Уравнение (22.6) даёт связь между временем t и местом - х, в котором указанное значение фазы осуществляется в данный момент. Определив из уравнения (22.6) 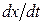, мы най­дём скорость, с которой перемещается данное значение фазы. Диффе­ренцируя(22.6), получаем:

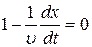, откуда следует 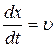(22.7)

Таким образом, скорость распространения волны в (22.1) есть скорость распространения фазы, вследствие чего её называет фазовой скоростью.

Уравнение (22.5) описывает волну, распространяющуюся в сторону возрастания х. Волна, распространяющаяся в противоположном нап­равлении, будет описываться аналогичным уравнением:

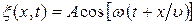(22.8)

Уравнения (22.5) и (22.8) обычно представляют в несколько ином виде, чтобы переменные х и t входили в уравнение волны симметрично. Для этого введем величину

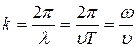, (22.9)

которую называют волновым числом.

С учётом (22.9) уравнение плоской волны (22.5) можно, записать в следующем виде:

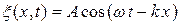(22.10)

Получим уравнение сферической волны. Рассуждая так же, как и в случае плоской волны, легко видеть что точки, лежащие на волновой поверхности радиуса R колеблются с фазой 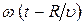. Можно показать, что амплитуда колебаний в сферической волне даже при отсутствии поглощения среды убывает по закону 1 /R (это является следствием того, что энергия источника волны распределяется по мере удаления от него по волновым поверхностям возрастающей площади). Поэтому уравнение сферической волныможно записать в виде:

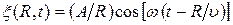(22.11)