Волновое уравнение для электромагнитных волн
Качественные соображения, указывающие на возможность существования электромагнитных волн, заключаются в следующем. Согласно уравнениям Максвелла, переменное электрическое поле (ток смещения) порождает магнитное, которое тоже должно быть переменным (чтобы порождаемое магнитное поле было постоянным необходимо постоянство производной 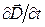 , чего не может быть в течение длительного времени). Переменное магнитное поле, в свою очередь, порождает переменное электрическое, и т.д.. В результате в пространстве должна возникнуть последовательность взаимных превращений электрического и магнитного полей. Этот процесс может быть бесконечным во времени и пространстве и представляет собой электромагнитную волну.
, чего не может быть в течение длительного времени). Переменное магнитное поле, в свою очередь, порождает переменное электрическое, и т.д.. В результате в пространстве должна возникнуть последовательность взаимных превращений электрического и магнитного полей. Этот процесс может быть бесконечным во времени и пространстве и представляет собой электромагнитную волну.
Покажем теперь более строго, что существование электромагнитных волн следует из уравнений Максвелла. Для этого необходимо из уравнений Максвелла получить волновое уравнение. С этой целью рассмотрим однородную, нейтральную (плотность заряда 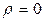 ), не проводящую (плотность тока
), не проводящую (плотность тока 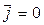 ) среду с постоянными диэлектрической
) среду с постоянными диэлектрической 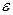 и магнитной
и магнитной 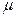 проницаемостями. С учетом этих ограничений будем использовать следующие соотношения:
проницаемостями. С учетом этих ограничений будем использовать следующие соотношения:
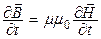 ;
; 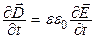 ;
; 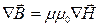 ;
; 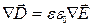 , (22.1)
, (22.1)
и представим уравнения Максвелла в виде:
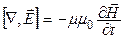 ; (22.2)
; (22.2)
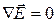 ; (22.3)
; (22.3)
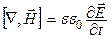 ; (22.4)
; (22.4)
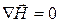 . (22.5)
. (22.5)
Возьмем ротор от обеих частей уравнения (22.2) и поменяем порядок дифференцирования в правой части:
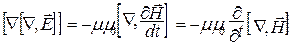 . (22.6)
. (22.6)
Подставим в (22.6) выражение для ротора 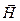 из уравнения (22.4):
из уравнения (22.4):
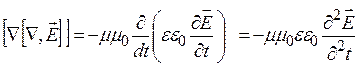 . (22.7)
. (22.7)
Воспользуемся тождеством векторного анализа: 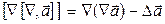 :
:
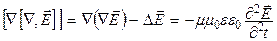 . (22.8)
. (22.8)
Учтем, что, согласно (22.3), 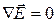 , и получим:
, и получим:
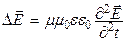 . (22.9)
. (22.9)
Величина 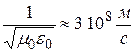 называется электродинамической постоянной и равна скорости света в вакууме. Поэтому (22.9) можно представить в виде:
называется электродинамической постоянной и равна скорости света в вакууме. Поэтому (22.9) можно представить в виде:
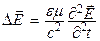 . (22.10)
. (22.10)
Это уравнение является волновым уравнением для вектора напряженности электрического поля.
Аналогичные преобразования можно провести, начиная с уравнения (22.4), и получить в результате волновое уравнение для вектора напряженности магнитного поля:
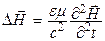 . (22.11)
. (22.11)
Таким образом, электрическое и магнитное поля могут существовать в виде электромагнитной волны, фазовая скорость распространения которой (квадратный корень из величины коэффициента перед производной по времени в волновом уравнении),
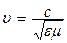 . (22.12)
. (22.12)
Дата добавления: 2021-01-11; просмотров: 536;











