Постулаты специальной теории относительности. Преобразования Лоренца

В релятивистской механике, также как и в классической, предполагается, что время однородно, а пространство однородно и изотропно.

Фундаментом специальной теории относительности являются два постулата Эйнштейна (1905):

1) Принцип относительности: законы природы инвариантны (неизменны) во всех инерциальных системах отсчета.

2) Принцип инвариантности скорости света: скорость света в вакууме одинакова в любых инерциальных системах отсчета.

Рассмотрим две инерциальные системы отсчета: S и S’. Пусть система S’ движется вдоль оси x со скоростью V относительно S. В начальный момент времени t = 0 системы совпадают.

Переход из системы S в S’ при малых скоростях (V << с) регламентируется преобразованиями Галилея (см. лекцию 4). В СТО эти классические преобразования уступают место преобразованиям Лоренца (1904).

S → S’
Преобразования Галилея	Преобразования Лоренца (14.1)
x’ = x – Vt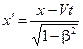
y’ = y	y’ = y
z’ = z	z’ = z
t’ = t	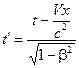, Здесь b = V/c.

Исследуя преобразования Лоренца, приходим к следующим выводам.

1) При малых скоростях (b << 1) преобразования Лоренца переходят в преобразования Галилея.

2) Расстояния и промежутки времени между двумя событиями меняются при переходе в новую инерциальную систему отсчета.

3) Пространственные и временные преобразования связаны друг с другом, то есть не являются независимыми [x’ = f(t) и t’ = f(x)]. Таким образом, в преобразованиях Лоренца используется не трехмерное пространство с присоединенным временем, а четырехмерное «пространство-время». Автор математического аппарата теории относительности Г. Минковский, поясняя неизбежность перехода к четырехмерному континууму «пространство-время», говорит: «Отныне понятие пространства самого по себе и времени самого по себе осуждены на отмирание и превращение в бледные тени, и только своего рода объединение этих двух понятий сохранит независимую реальность».

4) Если некоторая частица в системе отсчета S движется с постоянной скоростью 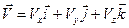, то составляющие её скорости в системе S’ будут равны:

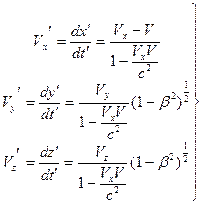. (14.2)

Это релятивистское правило сложения скоростей можно получить, воспользовавшись преобразованиями Лоренца (14.1). Предположим, что в системе S вдоль оси x движется фотон. Его скорость равна скорости света: V_x = с. Какой же будет скорость этого фотона 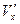в системе S’?

.

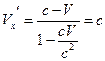Скорость фотона не меняется при переходе из одной инерциальной системы отсчета в другую. Этот результат свидетельствует о том, что скорость света инвариантна относительно преобразований Лоренца.