Газы реальные и идеальные

Общие сведения о свойствах и движении газов

Многие процессы, протекающие в металлургических печах, зависят от характера движения газов: теплообмен, распределения температур и давлений, диффузионные процессы и др.

Прежде чем рассмотреть законы движения газов вспомним о свойствах газов.

Газы сжимаемые и несжимаемые

В металлургии обычно используются печи негерметичные. Газы в таких печах находятся под давлением, которое незначительно отличается от атмосферного (порядка 0,2%).

В этих условиях можно считать, что объем газа практически не меняется при таком ничтожном изменении давления. Температура в печах в основном изменяется от участка к участку постепенно. Это дает основание пренебрегать влиянием температуры на отдельных участках.

Все вышесказанное позволяет рассматривать газы как несжимаемые среды.

Общим признаком несжимаемости газов является условие r=const. Это проявляется при обычных скоростях истечения (дозвуковых). Поэтому при изучении законов движения газов (в дозвуковых областях) мы будем рассматривать газы как несжимаемую среду.

Явления сжимаемости газов проявляется при высоких (сверхзвуковых) скоростях, когда r¹const.

Газы реальные и идеальные

Относительно газов существует понятие, что газы бывают реальные и идеальные.

Всем жидкостям и газам присуще свойство вязкости, т. е. способность оказывать сопротивление относительному движению (перемешиванию) частиц. Однако в некоторых газах (О₂, N₂, CO, CO₂ и др.) свойство вязкости проявляется слабо и им без большой погрешности можно пренебречь.

Было предложено и применено понятие идеального газа (идеальной жидкости) – абстрактной среды, лишенной свойства вязкости. Найдем зависимости V, r, W идеального газа от температуры и давления.

Из уравнения состояния идеальных газов (Клайперона) для одного и того же количества газа следует

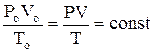, (1.1)

где V_o – объем, занимаемый газом при нормальных условиях, т. е. при Т_о=273 К и при атмосферном давлении Р_о=101332 Па (»10⁵ Па)

V – объем газа при давлении Р и температуре Т=Т_о+t₁=273+t₁ (здесь t₁ – температура по шкале цельсия, ⁰С);

Из уравнения (1.1) следует (зависимость расхода идеального газа от температуры и давления)

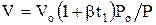, (1.2)

где b – коэффициент объемного расширения, град^-1;

b – относительное увеличение объема при нагреве газа на 1 град:

.

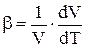Для идеального газа при постоянном давлении на основании закона Гей-Люссака можно написать:

,

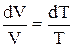откуда ;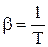

При 0 ⁰С; 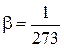, град^–1

Учитывая, что отношение массы газа М к его объему V, 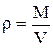есть плотность r, из уравнения (1.2) найдем

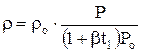, кг/м³ ( кГ сек²/м⁴) (1.3)

r_о – плотность газа при нормальных условиях, кг/м³ ;

r – плотность газа при давлении Р и температуре t₁;

Если под V понимать секундный расход (объем) газа (м³/с) и учесть, что скорость 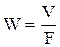, то при F=const зависимость скорости газа от температуры и давления выражается уравнением

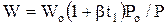, (1.4)

где W_o – скорость газа при нормальных условиях, м/с.

Если Р=Р_о, то

.

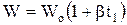В реальных газах молекулы подвержены силам взаимодействия и эти газы обладают вязкостью, т. е. свойством оказывать сопротивления относительно движению (перемещению) частиц.

При движении газа вязкость проявляется в возникновении сил внутреннего трения, что сопровождается потерей энергии.

Силу трения при движении газа можно подсчитать посчитать по формуле Ньютона: ,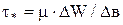

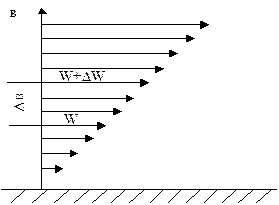
Рисунок 1

где t_*– сила трения, отнесенная к единице поверхности, разделяющая слои газа, Н/м²;

m – коэффициент пропорциональности, называемый коэффициентом динамической вязкости, Па*с;

DW – разностей скоростей на границах слоя толщиной Dв.

Наряду с коэффициентом динамической вязкости используют коэффициент кинетической вязкости n, м²/с.

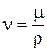, (1.5)

где r – плотность газа, кг/м³

С увеличением температуры вязкости газов растет

Лекция 2: