ИССЛЕДОВАНИЕ РАБОТЫ ТЕПЛООБМЕННОГО АППАРАТА ПРИ ИМИТАЦИОННОМ МОДЕЛИРОВАНИИ1

Данная глава предназначена для ознакомления студентов с процессом переноса тепла в одном из наиболее распространенных типов теплообменных аппаратов - рекуперативном аппарате с однофазными теплоносителями, а также методом интенсификации теплообмена в трубчатых ТА с помощью дискретно расположенных кольцевых диафрагм внутри трубы и соот- ветствующих им кольцевых канавок снаружи трубы. Для закрепления знаний студентам рекомендуется проделать лабораторную работу.

Предлагаемый материал и выдаваемая установкой информация позво- ляет ознакомиться с принципом работы ТА типа «труба в трубе» в режимах прямотока и противотока, оценить эффективность ТА в зависимости от гео- метрических и режимных параметров, определить коэффициенты теплопере- дачи и теплоотдачи по той стороне аппарата, где теплообмен менее интенси- вен. Кроме того, установка позволяет оценить эффективность применения интенсификации теплообмена.

Используется имитационное моделирование, позволяющее получить аналогичную информацию, как и в реальном эксперименте, отказавшись от дорогостоящей контрольно-измерительной аппаратуры, углубить и расши- рить изучаемые явления, получить более стабильные и наглядные результаты

данная глава составлена главным образом на материалах работы[2]

и значительно интенсифицировать учебный процесс благодаря мгно- венному переходу с одного режима работы установки на другой, при этом каждый студент может выполнять индивидуальное задание, используя мно- гочисленные варианты, введенные о микроЭВМ.

Оборудование изготовлено Днепропетровским специализированным конструкторским бюро ВСНПО «Союзучприбор».

Цель предлагаемой лабораторной работы – с помощью численного экс- перимента определить зависимость тепловой мощности ТА от схемы включения, вида теплоносителя, геометрических (диаметры наружной и внутренней труб, длина) и режимных параметров, определить коэффициент теплопередачи в зависимости от режимных параметров, коэффициент тепло- отдачи по одному из теплоносителей методом теплообменника, а также зави- симость тепловой мощности аппарата, коэффициентов теплопередачи и тепло- отдачи от геометрических параметров турбулизаторов.

4.1. Общие сведения

Теплообменные аппараты используются для передачи тепла от одного теплоносителя к другому. Теплоноситель, имеющий более высокую темпера- туру и отдающий тепло, называется горячим; теплоноситель, обладающий более низкой температурой и воспринимающий тепло, – холодным.

Все ТА по способу передачи тепла могут быть разделены на две боль- шие группы: поверхностные и контактные (рис. 4.1). В поверхностных аппара- тах теплоносители отделены друг от друга твердой стенкой (такие аппараты называются рекуперативными) либо поочередно контактируют с одной и той же стенкой (такие аппараты называются регенеративными). Эту стенку (по- верхность) называют поверхностью теплообмена.

Рис. 4.1. Классификация теплообменных аппаратов

В рекуперативном аппарате одна сторона поверхности теплообмена все время омывается горячим теплоносителем, другая – холодным. Тепло пере- дается от одного теплоносителя к другому через разделяющую их стенку. Направление теплового потока в стенке остается неизменным.

В регенеративном аппарате одна и та же поверхность теплообмена по- переменно омывается го одним, то другим теплоносителем. В период нагрева поверхности теплообмена, называемой насадкой регенератора, она контакти- рует с горячим теплоносителем и аккумулирует тепло, которое в период ох- лаждения отдает холодному теплоносителю. Направление теплового потока в стенках аппарата периодически меняется. В качестве насадки в таких аппара- тах могут использоваться шары, кольца, мелкие трубы, собранные в плотный пучок, иногда кирпичная кладка (например, в регенераторах мартеновских печей). Достоинствами таких аппаратов являются возможность размещения большой поверхности в единице объема (большая компактность) и осущест- вимость работы при высоких температурах (при использовании в качестве насадки высокотемпературных материалов), недостатками – плохая герме- тичность, неизбежность перемешивания теплоносителей, невозможность ра- боты при высоких давлениях рабочих сред.

В контактных теплообменных аппаратах передача тепла происходит при непосредственном контакте горячего и холодного теплоносителей, при этом теплообмен сопровождается массообменом. В аппаратах смесительного типа горячий и холодный теплоносители перемешиваются и образуют рас-

творы или смеси (примером таких аппаратов могут служить различного типа скрубберы или смесители горячей и холодной воды, используемые в систе- мах водоснабжения). В аппаратах барботажного типа теплоносители нахо- дятся в разных фазах и при контакте обмениваются теплом, практически не перемешиваясь между собой. Например, в градирнях капли разбрызгиваемой воды охлаждаются встречным потоком холодного воздуха, а в барботерях горячий пар охлаждается, поднимаясь через слой жидкости. Аппараты кон- тактного типа не могут применяться, если рабочие среды имеют разные дав- ления или вообще не могут перемешиваться.

Аппараты контактного и регенеративного типов не нашли широкого применения на практике. Основным типом теплообменников, используемых в различных областях техники, по-прежнему остаются рекуперативные аппа- раты, которые и будут дальше рассматриваться.

Рекуперативные теплообменные аппараты можно, в свою очередь, классифицировать:

1. По взаимному направлению потоков теплоносителей:

- прямоточные (прямоток), когда оба теплоносителя движутся парал- лельно в одном направлении (см. рис. 1.6, а);

- противоточные (противоток), когда оба теплоносителя движутся в противоположных направлениях (см. рис. 1.6, б);

- с перекрестный током, когда теплоносители движутся во взаимно перпендикулярных направлениях, однократно или многократно (см. рис. 1.6, в, д);

- со смешанным током (см. рис. 1.6, г)

- с более сложными схемами различного сочетания прямотока, проти- вотока и перекрестного тока (см. рис. 1.6, е, ж); на рисунке показаны вариан- ты с двумя противоположными ходами и перепуском.

2. По роду теплоносителей:

- аппараты, в которых оба теплоносителя не меняют своего агрегатного состояния (газо-газовые, жидко-жидкостные, газожидкостные);

- аппараты, в которых изменяется агрегатное состояние одного тепло- носителя, – конденсаторы (горячего теплоносителя), парогенераторы, испа- рители (холодного теплоносителя);

- аппараты, в которых изменяются агрегатные состояния обоих теплоносителей (конденсаторы- испарители).

3. По конструктивному оформлению:

- трубчатые;

- трубчато-ребристые;

- пластинчатые;

- пластинчато-ребристые;

- трубчато-пластинчатые.

Наиболее распространенной конструкцией являются трубчатые аппара- ты. Поверхность теплообмена таких аппаратов состоит из одной или не- скольких труб. Простейший теплообменник (типа «труба в трубе» состоит всего из одной трубы, которая внутри омывается одним теплоносителем, а снаружи – другим, протекающим в кольцевом пространстве между теплооб- менной трубой и кожухом. Если теплообменник состоит из нескольких труб, то они собираются в трубный пучок с помощью трубных досок. Трубы с трубными досками заключены в кожух.

Рассмотрим принципы теплового расчета рекуперативных теплообмен- ников с однофазными теплоносителями. Обычно при расчете аппарата опре- деляется либо поверхность теплообмена (конструкторский расчет), либо ко- личество переданного тепла и конечные температуры теплоносителей (пове- рочный расчет). В основе теплового расчета теплообменных аппаратов лежат уравнения теплового баланса и теплопередачи.

При стационарном режиме работы, если пренебречь утечками тепла в окружающую среду, передаваемый в аппарате тепловой поток равен умень- шению энтальпии горячего теплоносителя и увеличению энтальпии холодно- го теплоносителя:

dQ = -Gгdiг= Gхdiх; (4.1)

Q = G (i¢- i¢) = G (i¢- i¢) , (4.2)

г г г

х х х

где G – массовый расход теплоносителя, кг/с; i′ и i″ – энтальпии на входе и выходе из аппарата, Дж/кг, Q – тепловой поток, Вт. Индекс «г» обозначает горячий теплоноситель, «х» – холодный. Уравнение (4.2) – уравнение тепло- вого баланса.

Если вместо энтальпии ввести теплоемкость при постоянном давлении

cp, воспользовавшись соотношением di = cpdt, то уравнение (4.2) примет вид:

Q = G c

(t¢- t¢) = G c

(t¢- t¢), (4.3)

г pг г г

х pх х х

где

cpг

и cpх

– средние значения теплоемкостей горячего и холодного теп-

лоносителей соответственно в интервалах температур от

t¢х¢ . Уравнение (4.1) примет при этом вид:

tг¢ до

tг¢ и от

tх¢ до

dQ = -Gгcpгdtг= Gхcpг dtх. (4.4)

Иногда вводится понятие полных теплоемкостей массовых расходов горячего и холодного теплоносителей:

Wг= Gгcpг ,

Wх= Gх cpх

(4.5)

(раньше величину W называли водяным эквивалентом), Вт/К. Из вышеприведенных уравнений следует:

Wг = tх¢ - tх¢Wх tг¢ - tг¢

= - d t х , (4.6)

d t г

т.е. отношение изменения температур однофазных теплоносителей обратно пропорционально отношению их полных теплоемкостей (водяных эквива- лентов).

Для элемента поверхности теплообмена dF уравнение теплопередачи в дифференциальной форме записывается в виде:

dQ= k Δt dF, (4.7)

где k – коэффициент теплопередачи, Вт/(м2·К); Δt = tг – tх – текущий темпера- турный напор. Суммарный поток тепла через поверхность теплообмена рав- но:

F

Q = ò kÄtdF . (4.8)

Для определения Q необходимо знать распределение k и ΔT по поверх- ности теплообмена. Для однофазных теплоносителей коэффициент теплопе- редачи обычно изменяется незначительно, поэтому принимается постоянным по всей поверхности теплообмена. Тогда

F

Q = òÄtdF = k ÄtF , (4.9)

где средний по поверхности теплообмена температурный напор равен: 1 F

Ät = òÄtdF . (4.10)

F 0

Уравнение (4.9) является уравнением теплопередачи. Оно позволяет при конструкторском расчете определить поверхность теплообмена F.

Если в теплообменном аппарате коэффициент теплопередачи сущест- венно изменяется на отдельных участках поверхности теплообмена (как, на- пример, для аппаратов с кипением или конденсацией теплоносителя на части поверхности), вводится средний по поверхности коэффициент k.

Для плоской стенки коэффициент теплопередачи равен:

k = 1

1/ a1 + d / l + 1/ a2

, (4.11)

где α1, α2– коэффициенты теплопередачи; δ – толщина стенки; λ – коэффици- ент теплопроводности материала стенки; а для цилиндрической стенки при отнесении теплового потока соответственно к внутренней и наружной по- верхности равен:

k = 1

+ d1An × d2

+ d1

; (4.12)

a1 2l

k =

d1 a2d2

, (4.13)

1 × d2

+ d2An × d2+ 1

a1 d1 2l

d1 a2

где α1, α2– коэффициенты теплоотдачи внутри и снаружи трубы; d1 и d2 –

внутренний и наружный диаметры, Вт/(м2·К).

Если d2/d1< 1,8, то вполне допустимо использование определения k по формуле для плоской стенки (4.11):

Q = kpd 0 lÄt , (4.14)

где d0 = d2 при α1>> α2; d0 = d1 при α2>> α1и d0 = 0,5(d1+ d2) при α1= α2; здесь l – длина труб.

Если ввести линейный коэффициент теплопередачи для цилиндриче- ской стенки:

kl=

то

a1d1

+ 1 An × d2+

2l d1

a2d2

, (4.15)

Q = klplÄt . (4.16)

Необходимые для определения коэффициента теплоотдачи расчетные зависимости приводятся в учебниках, монографиях и справочниках.

Определим среднюю разность температур Ät

для простейших схем

движения теплоносителей – прямоточной (см. рис. 1.6, а) и противоточной (см. рис. 1.6, б). Характер изменения температур теплоносителей вдоль по- верхности теплообмена определяется схемой движения и соотношением теп- лоемкостей массовых расходов теплоносителей Wги Wх(водяных эквивален- тов). На рис. 4.2 показаны соответствующие кривые для прямотока и проти- вотока, построенные для постоянного коэффициента теплопередачи вдоль поверхности теплообмена F. Из рисунка видно, что для теплоносителей с большей теплоемкостью массового расхода температура вдоль поверхности теплообмена изменяется слабее.

Для прямотока (рис. 4.3) на участке dF температура горячего теплоно- сителя понизится на dtг, холодного – повысится на dtх. Согласно уравнению (4.4) имеем:

dtг

= - dQ ;

Wг

dtх

= - dQ . (4.17)

Wх

⎛ 1 + 1 ⎞ ⎛ 1 + 1 ⎞ −⎜⎜ ⎟⎟ dQ = -⎜ ⎟ ⎝ Wг Wх ⎠ ⎜ Gг cp Gх cp ⎟ ⎝ г х ⎠

Изменение температурного напора:

г

d(t

- tх) =

dQ . (4.18)

Используя уравнение (4.3) и выражая dQ через уравнение теплопереда- чи (4.7), можно получить, с учетом определения среднего по поверхности

температурного напора Ät

согласно уравнениям (4.9) и (4.10):

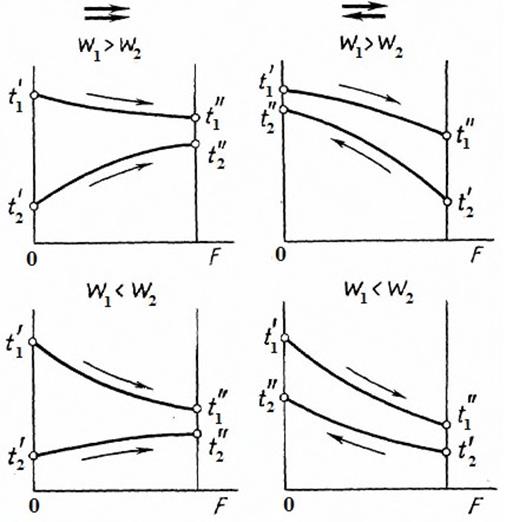
Рис. 4.2. Изменение температур теплоносителей вдоль поверхности теплооб- мена при прямотоке и противотоке

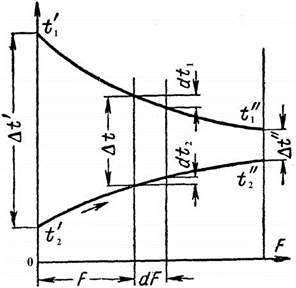
Рис. 4.3. Для определения среднелогарифмического температурного напора

(прямоток)

Ät= Ätлог =

(t¢- t¢)- (t¢- t¢)

. (4.19)

г х г х

ln tг¢ - tх¢

tг¢ - tх¢

Выражение (4.19) называется среднелогарифмическим температурным напором для прямотока.

⎛ 1 + 1 ⎞ ⎛ 1 + 1 ⎞ −⎜⎜ ⎟⎟dQ = -⎜ ⎟ ⎝ Wг Wх ⎠ ⎜ Gг cpг Gх cpг ⎟ ⎝ ⎠

При противотоке температуры обоих теплоносителей вдоль поверхно- сти теплообмена падают (см. рис. 4.2), и изменение температурного напора на участке dF равно

г

d(t

- tх

) = dt

- dtх=

dQ . (4.20)

г

При противотоке температурный напор по ходу горячего теплоносите- ля уменьшается, если Wг< Wх(см. рис. 4.2), и увеличивается, если Wг> Wх(см. рис. 4.2). Если же Wг= Wх, то температурный напор вдоль поверхности теплообмена не изменяется.

Используя уравнения (4.3) и (4.7), получаем

d(t - t ) kdF kdF

г х = -[(t¢- t¢)- (t¢- t¢)] = -[(t¢- t¢)- (t¢- t¢)] . (4.21)

tr - tх

г г х х Q

г х г х Q

Учитывая, что температурный напор вдоль поверхности F изменяется

от (t¢ - t¢)

до (t¢ - t¢)

(см. рис. 4.2), при интегрировании уравнения (4.21) полу-

г х г х

чаем:

ln tг¢ - tх¢

= -[(t¢- t¢)- (t¢- t¢)]kF . (4.22)

t¢- t¢

г х г х Q

г х

Тогда среднелогарифмический температурный напор при противотоке равен:

Ät- Ätлог =

(t¢ - t¢) - (t¢- t¢)

. (4.23)

г х г х

ln tг¢ - tх¢

tг¢ - tх¢

Вместо выражений (4.19) и (4.23) можно дать единую формулу:

Ätб - Ätм

Ätлог =

ln Ätб

Ätм

, (4.24)

справедливую как при прямотоке, так и при противотоке. Здесь Δtб – боль- ший температурный напор; Δtм– меньший температурный напор.

Если температура теплоносителей вдоль поверхности теплообмена из- меняется незначительно по сравнению с температурным напором, то темпе- ратурный напор можно определить как среднеарифметический между Δtби Δtм:

Ät =(Δtб+ Δtм). (4.25)

Формулу (4.25) используют, если Δtб/Δtм< 2.

При поверочном расчете теплообменного аппарата заданы температу-

ры теплоносителей на входе

tг¢ и

tх¢ , их расходы Gг и Gх, поверхность тепло-

обмена F и коэффициент теплопередачи k, а определяются конечные темпе-

ратуры теплоносителей

tг¢ и tх¢ и количество переданного тепла Q.

Для прямотока из уравнений (4.3) и (4.19) можно получить:

⎛ ⎞

ln tг¢ - tх¢

= -⎜ 1 + 1 ⎟kF

t¢- t¢

⎜ G c

G c ⎟

или

г х ⎝

г pг

х pх ⎠

kF ⎛

G c ⎞

t¢- t¢

-⎜1+

г pг ⎟

G c ⎜

G c ⎟

г х = 1 - e t¢- t¢

г pг ⎝

х pх ⎠ -1.

г х

Откуда, используя уравнение (4.3), получаем выражение для изменения тем-

ператур горячего и холодного теплоносителей:

⎛ ⎞

-kF ⎜1+ Gг cpг ⎟

G c ⎜

G c ⎟

tг¢ - tг¢ =

(t¢- t¢)1-e

г pг ⎝

г х

G c

х pх ⎠

; (4.26)

1+г pг

Gх cpх

⎛ ⎞

-kF ⎜1+ Gг cpг ⎟

G c ⎜

G c ⎟

tх¢ - tх¢ =

(t¢- t¢)1-e

г pг ⎝

г х

G c

х pх ⎠

. (4.27)

1+х pх

Gг cpг

При расчете промежуточных температур tг и tх в уравнения (4.26) и (4.27) вместо F подставляется текущее значение площади поверхности Fх, от- считываемое от входа теплоносителей.

Для противотока из уравнений (4.3) и (4.22) получаем:

⎛ G c ⎞

- kF ⎜ -г pг ⎟

t¢- t¢

G c ⎜1 G c ⎟

г х = e tг¢ - tх¢

г pг ⎝

х pх ⎠ .

Окончательные выражения для изменения температур теплоносителей имеют вид:

kF ⎛

G c ⎞

⎝

-⎜1- г pг ⎟

⎠

( ) 1 - e

Gгcpг ⎜

Gхcpх ⎟

t¢ - t¢ =

t¢- t¢

; (4.28)

г г г х

kF ⎛

G c ⎞

-⎜1- г pг ⎟

G c G c ⎜

G c ⎟

1 - г pг ×e Gхcpх

г pг ⎝

х pх ⎠

kF ⎛

G c ⎞

⎝

⎠

-⎜1- г pг ⎟

t¢ - t¢ =

(t¢- t¢)

1 - e

Gгcpг ⎜

Gхcpх ⎟

. (4.29)

х х г х

kF ⎛

G c ⎞

- ⎜1- г pг ⎟

G c ⎜ ⎟

х pх - e Gгcpг ⎝

Gг cpг

Gхcpх ⎠

При определении промежуточных температур tr и tх в противоточных теплообменниках F заменяется на Fхтолько в числителе уравнений (4.28) и (4.29), причем Fхотсчитывается от входа горячего теплоносителя.

Если температура теплоносителей вдоль поверхности теплообмена из- меняется незначительно (Δtб/Δtх< 2), то можно принять линейным ее распре- деление по длине, а средний температурный напор, определенный по уравне- нию (4.25), будет:

t Ät + Ät

⎛ t¢+ t¢

t¢+ t¢⎞ . (4.30)

Ä = б

м = ⎜ г г -

⎝ 2

х х ⎟

2 ⎠

Определив tr¢ и t¢х¢

из уравнения теплового баланса (4.3), получим:

⎛ Ät = (t¢ - t¢)- ⎜

г х ⎜ 2

1 ⎞

⎟

+ 2 ⎟ × Q . (4.31)

⎝ Gг cpг

Gх cpх ⎠

Подставив это выражение для Ät

решив его относительно Q, получим:

в уравнение теплопередачи (4.9) и

Q = tг¢ - tх¢

. (4.32)

1 + 1

+ 1

kF 2Gгcpг

2Gхcpх

Знание величины Q позволяет найти температуры на входе tг¢ и t¢х¢ .

Для сравнения прямотока с противотоком возьмем количество пере-

данного тепла при одинаковых kF,

Gгcpr, Gх cpх ,

tг¢ , tх¢ (рис. 4.4).

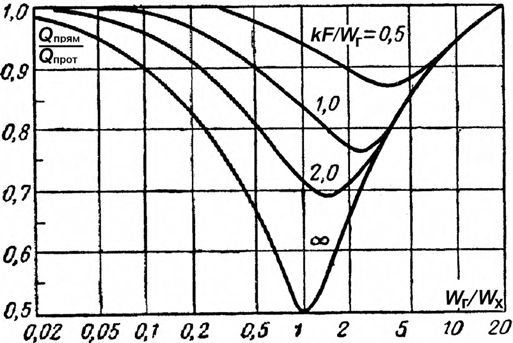
Рис. 4.4. Зависимость отношения предельных тепловых потоков при прямо- токе и противотоке Qпрям/Qпротот Wг/Wхи kF/Wг

Из графика видно, что эти схемы равноценны только при очень боль- ших и очень малых значениях Wг/Wх(практически при Wг/Wх< 0,5 и Wг/Wх>

10) или при очень малых значениях kF/Wг(меньше 0,1). Первое условие со-

ответствует малому изменению температуры одного из теплоносителей, во втором случае температурный напор значительно больше изменения темпе-

ратуры теплоносителя. Во всех остальных случаях при прочих равных усло- виях при противотоке передается больший тепловой поток, поэтому с данной точки зрения противоточная схема является предпочтительной. Следует так-

же обратить внимание на то, что только при противотоке можно получить t¢х¢ >

tг¢ (при прямотоке это в принципе невозможно).

Однако при противотоке температура поверхности теплообмена вблизи входа горячего теплоносителя оказывается более высокой, чем при прямото- ке. При высоких температурах горячего теплоносителя данное обстоятельст- во приходится учитывать.

К современным теплообменным аппаратам предъявляются повышенные требования по компактности, габаритам и массе. При заданных значениях тепловой мощности, расходов теплоносителей и гидравлических сопротивле- ний уменьшить габариты и массу аппаратов можно либо за счет увеличения коэффициентов теплопередачи, либо более плотной компоновкой (уменьше- ние диаметра труб и расстояния между ними). Но плотная компоновка ог- раничивается технологическими требованиями, поэтому возможности этого способа практически исчерпаны. Остается только уменьшение габаритных размеров и массы аппарата за счет интенсификации теплообмена.

Известно много методов интенсификации теплообмена. Среди них осо- бое место занимает закрутка потока в трубах с помощью различного рода винтовых вставок (закрученные ленты, шнеки) по всей длине трубы или на ее части, тангенциального подвода теплоносителя в трубу, лопаточных завери- телей, расположенных на входе или периодически. Кроме того, для интенси- фикации используются также криволинейные каналы (змеевиковые и спи- ральные). В ряде случаев для интенсификации теплообмена можно применять наложение на вынужденное течение колебаний расхода. При наличии в кана- ле акустического резонанса теплоотдача существенно увеличивается в зоне пучности скорости стоячей волны. При этом заметно возрастает и средняя теплоотдача.

Однако наиболее реальным, доступным и высокоэффективным способом

интенсификации теплообмена является искусственная турбулизация потока. При умеренном росте гидравлического сопротивления она значительно уве- личивает коэффициент теплоотдачи. Рассматриваемый метод интенсифика- ции теплообмена основан на детальном изучении структуры турбулентного течения в каналах.

На рис. 4.5 показано распределение вдоль радиуса трубы r безразмер- ных температур θ, скорости wх(r)/w0, плотности теплового потока q(r)/qw, массовой скороcти ρwx/(ρw)0и коэффициента турбулентного переноса им- пульса μт/μ при течении в трубе газа.

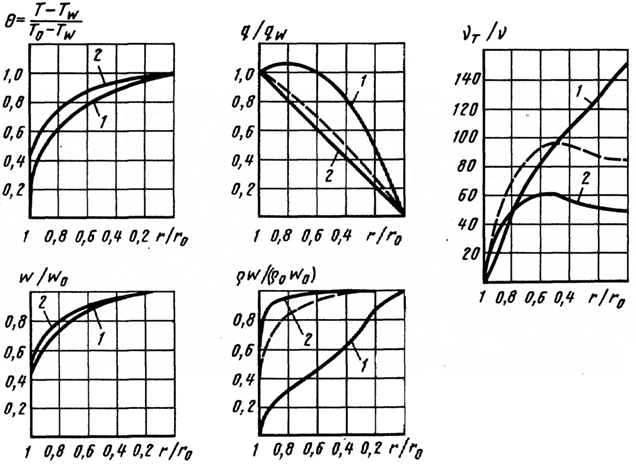
Рис. 4.5. Распределение параметров вдоль радиуса трубы при течении газа с Rew= 4,3·104; Pr = 0,7: 1 – нагревание воздуха при Tw = 1000 К, Tf = 154 К; 2 – охлаждение воздуха при Tw = 300 К, Tf = 902 К; 3 – изотермическое течение

Так как

q = (l + l

) ¶t, (4.33)

т ¶r

Где l – коэффициент теплопроводности; lт – коэффициент турбулентной те- плопроводности), а коэффициент теплоотдачи равен:

a = qw tw- t f

, (4.34)

среднемассовая температура потока равна:

Tf= t f

+ 273,15 =

r0

òrcpTwrdr

r0

òrcpwrdr

, (4.35)

то нетрудно заключить, что наибольшее влияние на α окажет увеличение λтв непосредственной близости от стенки. В пристенном слое толщиной (0,05…0,1)r0 среднее значение коэффициента турбулентной теплопроводно- сти λтне превышает 10% от максимального при данном числе Рейнольдса, а тепловой поток близок к максимальному. Поэтому в пристенном слое тол-

щиной (0,05…0,1)r0или высотой

y+ = y n

tw/ r

» 60 ¸160

(y – расстоя-

ние от стенки; ν – коэффициент кинематической вязкости; τw – касательное напряжение на стенке) расходуется 60...70% располагаемого температурного напора. Чем больше число Прандтля, тем на более узкий пристенный слой целесообразно воздействовать. Следовательно, наибольшей интенсификации теплоотдачи можно добиться, увеличивая λтименно в таких пристенных сло-

ях. В то же время ясно, что дополнительная турбулизация ядра потока (где λтвелико, а q << qw) мало увеличит теплоотдачу, хотя и приведет к большому росту гидравлических потерь.

Эффективным методом интенсификации теплоотдачи является создание в пристенной области отрывных зон. Наилучшие результаты получаются при дискретной турбулизации потока на стенках каналов, причем источниками турбулентных вихрей должны служить плавно очерченные выступы или ка- навки с высотой y+ = 60 ÷ 50. Их не рекомендуется располагать слишком час- то (t/h = 5 ÷ 10, где h – шаг, а t – высота турбулизатора), так как возникающие при этом за турбулизатором пульсации не успеют заметно затухнуть на пути к следующему турбулизатору и будут диффундировать в ядро, увеличивая тем самым интенсивность пульсаций. Подобное явление имеет место в шеро- ховатых трубах и ведет к значительному росту гидравлических потерь при небольшом повышении теплоотдачи.

Если же увеличить расстояние между турбулизаторами, то дополни- тельно возникшие в зоне вихри и генерируемые при их периодическом раз- рушении турбулентные пульсации переносятся потоком близко к стенке, по- вышая λттолько около нее, а значит, интенсификация теплоотдачи будет дос- тигнута ценой минимальных гидравлических потерь. При слишком большом (t/h = 50 ÷ 100) расстоянии между турбулизаторами дополнительная турбу- лентность успевает заметно затухнуть на некотором расстоянии от турбули- затора, и остальной участок канала до следующего турбулизатора по струк- туре потока будет мало отличаться от гладкого канала.

Максимальное увеличение теплоотдачи Nu/Nuгли гидравлического со- противления ξ/ξгл по сравнению с гладкой поверхностью достигается при t/h

@ 10, причем максимум Nu/Nuгл не зависит от формы турбулизатора, а мак-

симум ξ/ξгл сильно зависит (он минимален при плавной форме турбулизато- ра).

Для трубчатых теплообменных аппаратов в каналах любого поперечно- го сечения часто используют следующий рациональный метод интенсифика-

ции теплообмена. На наружной поверхности теплообменных труб накаткой наносят периодически расположенные кольцевые канавки (рис. 4.6). При этом на внутренней поверхности труб образуются кольцевые диафрагмы с плавной конфигурацией. Диаграммы и кольцевые канавки турбулизируют по- ток в пристенном слое и обеспечивают интенсификацию теплообмена как снаружи, так и внутри труб. При этом не увеличивается наружный диаметр труб, что позволяет использовать их в тесных пучках и не менять сущест- вующей технологии сборки трубчатых ТА. Данные поверхности теплообмена применяются в трубчатых аппаратах, работающих на газах и жидкостях, а также при кипении и конденсации теплоносителей.

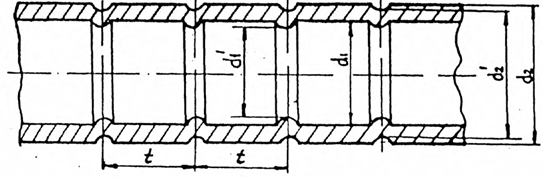
Рис. 4.6. Профиль теплообменных труб с накаткой

Возникающие на таких поверхностях отрывные зоны как источники вихре- вых структур формируют неустойчивость вязкостных течений, расширяя тем са- мым переходную область ( Re = 2 000 ÷ 5 000), в которой достигаются наи- более эффективные соотношения между ростом коэффициента теплоотдачи и гидравлического сопротивления (Nu/Nuгл= 2,83 при ξ/ξгл= 2,85). На основе выявленного механизма взаимодействия искусственных турбулизаторов с потоком в области перехода и слаборазвитой турбулентности установлено, что рациональная интенсификация достигается в этих условиях при доста-

точно больших высотах диафрагм ( d1¢ / d1

= 0,92) и оптимальном шаге t/d1 =

1. В определенном диапазоне соответствующих размеров и расположений турбулизаторов рост теплоотдачи больше роста гидравлического сопротив- ления по сравнению с аналогичным гладким каналом.

Использование практически реализуемого соотношения Nu/Nuгл< ξ/ξгл позволяет при заданных значениях тепловой мощности и гидравлического сопротивления теплообменника уменьшить не только объем аппарата, но и площадь его поперечного сечения. Применение данного метода интенсифи- кации позволяет уменьшить объем теплообменного аппарата примерно в 2 раза при неизменных значениях тепловой мощности и мощности на прокачку теплоносителя. Значительный эффект наблюдается в переходной области. При этом объем теплообменного аппарата может быть уменьшен в 2,5 раза.

Область с Nu/Nuгл> ξ/ξглимеет место и при продольном обтекании пучков труб с кольцевыми канавками, вплоть до Nu/Nuгл= 1,4 ÷ 1,5 при от- носительном шаге размещения труб в пучке S/d2 = 1,2. При этом объем аппа- рата может быть снижен на одну треть. Накатка труб с различными соотно- шениями между глубиной канавок снаружи и высотой диафрагм внутри труб позволяет получить оптимальную интенсификацию теплоотдачи по обеим поверхностям теплообмена при различных шагах размещения труб в пучке (S/d2 = 1,05 ÷ 1,5).

Опытные данные по средней теплоотдаче при нагревании и охлажде- нии газов обобщаются следующими зависимостями:

при

d1¢ / d1 = 0,88 ÷ 0,98, t/d1 = 0,25 ÷ 0,8*

Nu ⎡